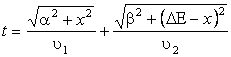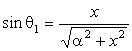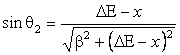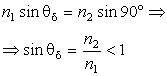ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΣΕΡΡΩΝ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ
Φ υ σ ι κ ή Ι Ι
Δρ. Χρήστος Λ. Βοζίκης
Επιστημονικός Συνεργάτης
Τομέας Τηλεπικοινωνιών και Δικτύων
Σέρρες 2008
Ο επιστήμονας δεν μελετά την φύση επειδή αυτό είναι χρήσιμο.
Την μελετά γιατί αυτό τον ευχαριστεί.
Και τον ευχαριστεί γιατί η φύση είναι όμορφη.
Εάν η φύση δεν ήταν όμορφη, τότε δεν θα άξιζε τον κόπο να την γνωρίσουμε.
Και αν δεν άξιζε τον κόπο να την γνωρίσουμε, τότε δεν θα άξιζε τον κόπο να ζούμε!
Henri Poincaré
Το παρόν αποτελεί μια προσπάθεια για την μετατροπή σε ηλεκτρονική μορφή των διδακτικών σημειώσεων του μαθήματος “Φυσική ΙΙ” που διδάσκεται στο Β΄ εξάμηνο του Τμήματος Πληροφορικής και Επικοινωνιών του Τ.Ε.Ι. Σερρών.
Στην αρχή του Κεφαλαίου 1 περιέχονται ορισμένα θέματα ηλεκτρομαγνητισμού τα οποία έχουν ήδη διδαχθεί οι σπουδαστές στα πλαίσια του μαθήματος “Φυσική Ι” του Α΄ εξαμήνου. Η υπενθύμιση των θεμάτων αυτών κρίθηκε απαραίτητη για την σωστή δομή και συνέχεια της ύλης.
Έγινε προσπάθεια ώστε ο μαθηματικός φορμαλισμός είναι να είναι όσο το δυνατόν πιο απλός, αποφεύγοντας αποδείξεις εξισώσεων που το μαθηματικό τους επίπεδο προϋποθέτει γνώσεις που δεν κατέχονται από τους πρωτοετείς σπουδαστές του Τμήματος.
Ελπίζω πως ο τρόπος παρουσίασης των θεμάτων επιτρέπει την εύκολη κατανόηση της ύλης. Είναι όμως βέβαιο πως ορισμένα σημεία χρειάζονται περισσότερη ανάλυση και βελτίωση. Για το λόγο αυτό κάθε υπόδειξη σχετικά με λάθη, παραλείψεις αλλά και υποδείξεις για την βελτίωση του θα γίνει ευχαρίστως δεκτή.
Χρήστος
Βοζίκης
1. Ηλεκτρομαγνητικές Ταλαντώσεις
1.1. Εισαγωγή
Στο Α΄ εξάμηνο, στα πλαίσια του μαθήματος “ Φυσική Ι ” εξετάστηκαν οι ιδιότητες των ηλεκτρικών πεδίων και των στοιχείων των ηλεκτρικών κυκλωμάτων. Παρουσιάστηκαν επίσης τα μαγνητικά πεδία και τα φαινόμενα που σχετίζονται με την δημιουργία τους και την σχέση τους με τον ηλεκτρισμό.
Στο παρόν κεφάλαιο, αφού αναφερθούμε, εν συντομία, σε μερικά φαινόμενα του ηλεκτρομαγνητισμού, για να θυμηθούμε μερικές βασικές έννοιες και σχέσεις, θα μελετήσουμε τις ιδιότητες κυκλωμάτων που αποτελούνται από αντιστάσεις και πυκνωτές ή πηνία. Τέλος θα αναφερθούμε στην ιδιαίτερη κατηγορία κυκλωμάτων τα οποία, αποτελούμενα από πυκνωτές και πηνία, εμφανίζουν ηλεκτρομαγνητικές ταλαντώσεις, δηλαδή η ενέργεια τους εναλλάσσεται μεταξύ της ενέργειας του ηλεκτρικού πεδίου του πυκνωτή και του μαγνητικού πεδίου του πηνίου.
1.2. Ηλεκτρικό πεδίο
Είναι γνωστό ότι ένα φορτίο Q δημιουργεί στο χώρο ένα πεδίο
δυνάμεων. Ένα πεδίο, δηλαδή, στο οποίο αν βρεθεί ένα οποιοδήποτε άλλο φορτίο q ασκείται επάνω του δύναμη ![]() . Το πεδίο αυτό επειδή δημιουργείται
από ηλεκτρικό φορτίο λέγεται ηλεκτρικό πεδίο.
. Το πεδίο αυτό επειδή δημιουργείται
από ηλεκτρικό φορτίο λέγεται ηλεκτρικό πεδίο.
Η δύναμη ![]() που ασκείται πάνω στο φορτίο q λόγω του πεδίου που δημιουργεί το
φορτίο Q έχει διεύθυνση πάνω στην ευθεία που συνδέει τα δύο φορτία και είναι ίση
με :
που ασκείται πάνω στο φορτίο q λόγω του πεδίου που δημιουργεί το
φορτίο Q έχει διεύθυνση πάνω στην ευθεία που συνδέει τα δύο φορτία και είναι ίση
με :
|
|
(1.1) |
όπου r η απόσταση των δύο φορτίων και ![]() το μοναδιαίο διάνυσμα στην
ευθεία που συνδέει τα δύο φορτία με φορά από το φορτίο Q στο φορτίο q.
το μοναδιαίο διάνυσμα στην
ευθεία που συνδέει τα δύο φορτία με φορά από το φορτίο Q στο φορτίο q.
Φυσικά ηλεκτρικό πεδίο δεν δημιουργείται μόνο από ακίνητα σημειακά φορτία, όπως στην προηγούμενη παράγραφο, αλλά και από κινούμενα ή και από συνεχείς κατανομές φορτίων (όπως για παράδειγμα από τα φορτία στους οπλισμούς ενός πυκνωτή).
Ως ένταση του ηλεκτρικού πεδίου ![]() σε ένα σημείο του χώρου Σ (στον
οποίο υπάρχει το πεδίο) ορίζουμε την δύναμη
σε ένα σημείο του χώρου Σ (στον
οποίο υπάρχει το πεδίο) ορίζουμε την δύναμη ![]() που εξασκείται λόγω του πεδίου σε ένα μοναδιαίο
φορτίο που βρίσκεται στο συγκεκριμένο σημείο Σ. Ισοδύναμα θα μπορούσαμε να
πούμε πως ένταση του ηλεκτρικού πεδίου σε ένα σημείο του χώρου Σ
είναι το πηλίκο της δύναμης
που εξασκείται λόγω του πεδίου σε ένα μοναδιαίο
φορτίο που βρίσκεται στο συγκεκριμένο σημείο Σ. Ισοδύναμα θα μπορούσαμε να
πούμε πως ένταση του ηλεκτρικού πεδίου σε ένα σημείο του χώρου Σ
είναι το πηλίκο της δύναμης ![]() που ασκείται πάνω σε ένα φορτίο q που βρίσκεται στο σημείο αυτό, προς
το φορτίο q. Δηλαδή
που ασκείται πάνω σε ένα φορτίο q που βρίσκεται στο σημείο αυτό, προς
το φορτίο q. Δηλαδή
|
|
(1.2) |
Παράλληλα με τον ορισμό της έντασης
του ηλεκτρικού πεδίου μπορούμε να ορίσουμε την ροή του ηλεκτρικού πεδίου
ή αλλιώς ηλεκτρική ροή. Αν θεωρήσουμε μία επιφάνεια S τότε το μέτρο της ηλεκτρικής ροής
ενός πεδίου ![]() που περνά από την επιφάνεια S δίνεται από την σχέση :
που περνά από την επιφάνεια S δίνεται από την σχέση :
|
|
(1.3) |
Το ολοκλήρωμα της προηγούμενης σχέσης είναι ένα επιεπιφάνειο
ολοκλήρωμα, δηλαδή ένα ολοκλήρωμα που υπολογίζεται πάνω στην επιφάνεια S. Για απλή επίπεδη επιφάνεια και για ![]() που παραμένει σταθερό σε όλα τα
σημεία της επιφάνειας η ηλεκτρική ροή είναι ίση με
που παραμένει σταθερό σε όλα τα
σημεία της επιφάνειας η ηλεκτρική ροή είναι ίση με
όπου θ η γωνία που σχηματίζουν το κάθετο διάνυσμα στην
επιφάνεια S με το διάνυσμα ![]() .
.
1.3. Μαγνητικό πεδίο
Ένα κινούμενο ηλεκτρικό φορτίο ή ισοδύναμα ένας αγωγός που διαρρέεται από ηλεκτρικό ρεύμα δημιουργεί γύρω του ένα πεδίο δυνάμεων. Το πεδίο αυτό ασκεί δυνάμεις σε άλλα κινούμενα φορτία (ή αγωγούς που διαρρέονται από ηλεκτρικό ρεύμα). Το πεδίο αυτό ονομάζεται μαγνητικό πεδίο.
Ανάλογα προς την ένταση του ηλεκτρικού πεδίου μπορούμε να ορίσουμε την ένταση
του μαγνητικού πεδίου ![]() ή όπως αλλιώς
αναφέρεται την μαγνητική επαγωγή. Έστω λοιπόν ένα φορτίο q που κινείται στον χώρο του
μαγνητικού πεδίου
ή όπως αλλιώς
αναφέρεται την μαγνητική επαγωγή. Έστω λοιπόν ένα φορτίο q που κινείται στον χώρο του
μαγνητικού πεδίου ![]() με ταχύτητα
με ταχύτητα ![]() .
Η δύναμη που ασκείται στο φορτίο από το μαγνητικό πεδίο είναι ίση με
.
Η δύναμη που ασκείται στο φορτίο από το μαγνητικό πεδίο είναι ίση με
|
|
(1.5) |
Η δύναμη ![]() είναι κάθετη στο επίπεδο
που ορίζουν τα διανύσματα
είναι κάθετη στο επίπεδο
που ορίζουν τα διανύσματα ![]() και
και ![]() και
έχει μέτρο :
και
έχει μέτρο :
|
|
(1.6) |
όπου θ η γωνία των διανυσμάτων ![]() και
και
![]() .
.
Πώς όμως δημιουργείται αυτό το πεδίο ![]() που
επηρεάζει τα κινούμενα φορτία και τους ρευματοφόρους αγωγούς; Οι Biot και Savart μετά από πειράματα κατέληξαν ότι
όταν ένας αγωγός διαρρέεται από ρεύμα εντάσεως Ι τότε κάθε στοιχειώδες τμήμα
του μήκους
που
επηρεάζει τα κινούμενα φορτία και τους ρευματοφόρους αγωγούς; Οι Biot και Savart μετά από πειράματα κατέληξαν ότι
όταν ένας αγωγός διαρρέεται από ρεύμα εντάσεως Ι τότε κάθε στοιχειώδες τμήμα
του μήκους ![]() δημιουργεί σε ένα σημείο Σ
του χώρου (εκτός του αγωγού) μαγνητικό πεδίο που η έντασή του
δημιουργεί σε ένα σημείο Σ
του χώρου (εκτός του αγωγού) μαγνητικό πεδίο που η έντασή του ![]() δίνεται
από την σχέση :
δίνεται
από την σχέση :
|
|
(1.7) |
όπου r το διάνυσμα που συνδέει το στοιχειώδες τμήμα ![]() με
το σημείο Σ και μ0 μία σταθερή που ονομάζεται μαγνητική διαπερατότητα
του κενού ή απλά διαπερατότητα του κενού και είναι ίση με 4π × 10 -7 Wb ×
A-1 × m.
με
το σημείο Σ και μ0 μία σταθερή που ονομάζεται μαγνητική διαπερατότητα
του κενού ή απλά διαπερατότητα του κενού και είναι ίση με 4π × 10 -7 Wb ×
A-1 × m.
Χρησιμοποιώντας τον νόμο των Biot - Savart μπορούμε να υπολογίσουμε το μαγνητικό πεδίο που δημιουργούν αγωγοί διαφόρων τύπων. Έτσι ένας ευθύγραμμος, θεωρητικά απείρου μήκους, αγωγός δημιουργεί σε απόσταση r μαγνητικό πεδίο έντασης :
|
Σχήμα 1.1 Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού. |
Οι δυναμικές γραμμές του πεδίου είναι κύκλοι με κέντρο τον
αγωγό. Έτσι, αν ο αγωγός ήταν κάθετος στο βιβλίο και η ένταση Ι είχε φορά από
το βιβλίο προς τον αναγνώστη, η ένταση του πεδίου θα είχε την φορά που
παρουσιάζεται στο Σχήμα 1.1.
Ένας κυκλικός αγωγός ακτίνας R που διαρρέεται από ρεύμα εντάσεως Ι δημιουργεί στον χώρο μαγνητικό πεδίο όμοιο με αυτό του Σχήματος 1.2. Το πεδίο αυτό προκύπτει από την ενισχυτική επιπρόσθεση των στοιχειωδών πεδίων που δημιουργούν κάθε ένα από τα στοιχειώδη τμήματα του αγωγού. Η ένταση του μαγνητικού πεδίου στο κέντρο του κυκλικού αγωγού αποδεικνύεται ότι δίνεται από την σχέση:
|
|
(1.9) |
Στην περίπτωση ενός σωληνοειδούς αγωγού ή, όπως συνήθως
ονομάζεται, ενός πηνίου, μήκους ![]() που αποτελείται από Ν σπείρες
και διαρρέεται από ρεύμα εντάσεως Ι, το μαγνητικό πεδίο (Σχήμα
1.3) στο εσωτερικό του παρουσιάζεται ομογενές και έχει ένταση :
που αποτελείται από Ν σπείρες
και διαρρέεται από ρεύμα εντάσεως Ι, το μαγνητικό πεδίο (Σχήμα
1.3) στο εσωτερικό του παρουσιάζεται ομογενές και έχει ένταση :
Αντίστοιχα με την ηλεκτρική ροή μπορούμε να ορίσουμε την μαγνητική ροή ή ροή του μαγνητικού πεδίου που διαρρέει μία επιφάνεια S ως το επιεπιφάνειο ολοκλήρωμα
Φυσικά στην περίπτωση σταθερού πεδίου έντασης B και επίπεδης επιφάνειας εμβαδού S η προηγούμενη σχέση ανάγεται στην αντίστοιχη της (1.4) όπου απλώς αντικαθιστούμε το Ε με το Β.
1.4. Επαγωγή και αυτεπαγωγή
Αν ένας αγωγός βρίσκεται εντός μαγνητικού πεδίου και η μαγνητική ροή που διαπερνά τον αγωγό μεταβάλλεται με τον χρόνο τότε στα άκρα του αγωγού εμφανίζεται ηλεκτρεγερτική δύναμη.
Το φαινόμενο αυτό ονομάζεται επαγωγή και η ηλεκτρεγερτική δύναμη που εμφανίζεται στα άκρα του αγωγού δίνεται από τον νόμο της επαγωγής του Faraday:
Από τον ορισμό του Φm βλέπουμε ότι φαινόμενα επαγωγής μπορούμε να έχουμε είτε όταν μεταβάλλεται το μαγνητικό πεδίο είτε όταν μεταβάλλεται η επιφάνεια του αγωγού (για παράδειγμα όταν αλλάζει ο προσανατολισμός του αγωγού δηλαδή η γωνία θ). Το αρνητικό πρόσημο στην προηγούμενη σχέση οφείλεται στο γεγονός ότι η επαγόμενη ηλεκτρεγερτική δύναμη είναι τέτοια ώστε να τείνει να δημιουργήσει ρεύμα το οποίο θα παράγει μαγνητική ροή που αντιτίθεται στην μεταβολή της Φm.
Ας πάρουμε τώρα ένα πηνίο που διαρρέεται από ρεύμα έντασης Ι. Το πηνίο δημιουργεί ένα μαγνητικό πεδίο σύμφωνα με την σχέση (1.10). Αν μεταβάλουμε το ρεύμα Ι (ή αν διακόψουμε τελείως το ρεύμα) τότε το μαγνητικό πεδίο μεταβάλλεται. Ταυτόχρονα μεταβάλλεται η μαγνητική ροή Φm που διαρρέει το πηνίο. Σύμφωνα λοιπόν με την σχέση (1.12) δημιουργείται στον αγωγό ηλεκτρεγερτική δύναμη η οποία δημιουργεί ρεύμα που αντιτίθεται στην μεταβολή της έντασης Ι. Το ίδιο θα συμβεί αν αρχικά το πηνίο δεν διαρρέεται από ρεύμα και κλείσουμε τον διακόπτη δίνοντας ρεύμα στο κύκλωμα. Και στην περίπτωση αυτή η επαγόμενη ηλεκτρεγερτική δύναμη αντιτίθεται στην μεταβολή της έντασης και το ρεύμα Ι δεν παίρνει αμέσως την μέγιστη τιμή του. Το φαινόμενο αυτό ονομάζεται αυτεπαγωγή.
Στην περίπτωση ενός πηνίου με Ν σπείρες η ηλεκτρεγερτική δύναμη από αυτεπαγωγή δίνεται από την σχέση :
Η σταθερή αναλογία L ονομάζεται συντελεστής αυτεπαγωγής του πηνίου και εξαρτάται από τα φυσικά και γεωμετρικά χαρακτηριστικά του πηνίου.
1.5. Κυκλώματα RC.
Μετά την σύντομη αναφορά σε μερικές βασικές έννοιες και φαινόμενα του ηλεκτρομαγνητισμού θα προχωρήσουμε στην μελέτη της συμπεριφοράς ορισμένων βασικών κυκλωμάτων.
Στο Σχήμα 1.4 παρουσιάζεται ένα απλό κύκλωμα RC. Ένα κύκλωμα RC αποτελείται ένα πυκνωτή χωρητικότητας C και μία αντίσταση R συνδεδεμένα σε σειρά. Στο κύκλωμα συνδέεται πηγή συνεχούς ηλεκτρικού ρεύματος (μπαταρία) ηλεκτρεγερτικής δύναμης E.
1.5.1. Φόρτιση Πυκνωτή
Ας υποθέσουμε ότι ο πυκνωτής δεν είναι αρχικά φορτισμένος. Κλείνουμε τον διακόπτη Δ την χρονική στιγμή t=0 και ο πυκνωτής αρχίζει να φορτίζεται. Γνωρίζουμε ότι στο συνεχές ρεύμα ο πυκνωτής δρα σαν ανοικτός διακόπτης. Tα φορτία δεν “πηδούν” από τον ένα οπλισμό του πυκνωτή στον άλλο. Γενικά το κύκλωμα δεν διαρρέεται από ρεύμα αλλά στην αρχή, μέχρις ότου ο πυκνωτής φορτιστεί με το μέγιστο φορτίο, ηλεκτρικά φορτία κινούνται από τον ένα οπλισμό στον άλλο μέσω του κυκλώματος της αντίστασης της μπαταρίας και του διακόπτη. Έτσι το κύκλωμα εμφανίζεται να διαρρέεται από ρεύμα έντασης Ι. Το μέγιστο φορτίο του πυκνωτή φυσικά εξαρτάται από την χωρητικότητα του πυκνωτή και την τιμή της ηλεκτρεγερτικής δύναμης της μπαταρίας.
Αν εφαρμόσουμε τον δεύτερο κανόνα του Kirchhoff αφού κλείσουμε τον διακόπτη και πριν φορτιστεί πλήρως ο πυκνωτής και διακοπεί το ρεύμα, τότε έχουμε
όπου I R η πτώση τάσης στην αντίσταση και q/C η τάση στα άκρα του πυκνωτή.
Την στιγμή t=0 που κλείνουμε τον διακόπτη το φορτίο στον πυκνωτή είναι q=0 και από την προηγούμενη σχέση βρίσκουμε την μέγιστη τιμή του ρεύματος
Αντίστοιχα από τη στιγμή που θα φορτιστεί πλήρως ο πυκνωτής το ρεύμα μηδενίζεται, δηλαδή Ι=0 και από την σχέση (1.14) βρίσκουμε το μέγιστο φορτίο Q του πυκνωτή :
Στις ενδιάμεσες χρονικές στιγμές η ένταση του ρεύματος μειώνεται βαθμιαία από Ι=Ι0 στο Ι=0 και το φορτίο αυξάνεται από q=0 σε q=Q. Για να βρούμε την σχέση που μας δίνει την χρονική εξάρτηση της έντασης του ρεύματος Ι(t) και του φορτίου q(t), παραγωγίζουμε την εξίσωση (1.14) ως προς τον χρόνο t.
Η ένταση του ρεύματος Ι είναι ίση με την μεταβολή του φορτίου
![]() και η σχέση (1.17)
γράφεται
και η σχέση (1.17)
γράφεται
Μια που τα R και C είναι σταθερές, η εξίσωση (1.18) είναι μία απλή διαφορική εξίσωση πρώτης και λύνεται με απλή ολοκλήρωση χρησιμοποιώντας για αρχική συνθήκη t=0 την σχέση (1.15),
|
|
(1.19) |
Από την οποία καταλήγουμε τελικά ότι η ένταση του ρεύματος δίνεται από την σχέση :
Αν θέλουμε να βρούμε την σχέση για το
φορτίο του πυκνωτή δεν έχουμε παρά να χρησιμοποιήσουμε τις σχέσεις ![]() και
και ![]() . Έτσι έχουμε
. Έτσι έχουμε
|
|
(1.21) |
γνωρίζοντας ότι ![]() βρίσκουμε
βρίσκουμε
όπου αντικαταστήσαμε το ![]() από την σχέση (1.16)
από την σχέση (1.16)
Η ποσότητα RC που υπάρχει στον εκθέτη των εξισώσεων (1.20) και (1.22) ονομάζεται σταθερά χρόνου του κυκλώματος και συμβολίζεται με τ και μας δίνει σε πόσο χρόνο από την στιγμή που θα κλείσουμε τον διακόπτη του κυκλώματος το ρεύμα θα γίνει ίσο με το 1/e » 0.37 της μέγιστης τιμής του Ι0.
Στο Σχήμα 1.5 παρουσιάζονται οι γραφικές παραστάσεις της μεταβολής της έντασης του ρεύματος Ι (αριστερά) όπως αυτή δίνεται από την σχέση (1.20) και του φορτίου στους οπλισμούς του πυκνωτή (δεξιά) όπως αυτή δίνεται από την σχέση (1.22) συναρτήσει του χρόνου t. Όπως βλέπουμε και από το Σχήμα 1.5 η ένταση του ρεύματος μειώνεται εκθετικά και μηδενίζεται μετά από άπειρο χρόνο ενώ ταυτόχρονα το φορτίο του πυκνωτή αυξάνει και τείνει ασυμπτωτικά στην μέγιστη τιμή του.
|
Σχήμα 1.5 H χρονική μεταβολή της έντασης Ι του ρεύματος και του φορτίου q στους οπλισμούς του πυκνωτή κατά την φόρτιση του πυκνωτή στο κύκλωμα RC. |
Το παραγόμενο από την μπαταρία έργο κατά την διάρκεια της φόρτισης είναι
|
|
(1.23) |
από αυτό το ![]() καταναλώνεται πάνω στην αντίσταση ενώ το
υπόλοιπο
καταναλώνεται πάνω στην αντίσταση ενώ το
υπόλοιπο ![]() αποθηκεύεται ως ενέργεια του πυκνωτή. Η ενέργεια
λοιπόν που αποθηκεύεται στον ηλεκτρικό πεδίο του πυκνωτή είναι
αποθηκεύεται ως ενέργεια του πυκνωτή. Η ενέργεια
λοιπόν που αποθηκεύεται στον ηλεκτρικό πεδίο του πυκνωτή είναι
Ας υποθέσουμε τώρα ότι έχουμε ένα φορτισμένο πυκνωτή και τον συνδέουμε σε κύκλωμα με αντίσταση R όπως του Σχήματος 1.6. Μόλις κλείσουμε τον διακόπτη Δ ο πυκνωτής αρχίζει να εκφορτίζεται και ρεύμα έντασης Ι διαπερνά το κύκλωμα.
Από τον δεύτερο νόμο του Kirchhoff γνωρίζουμε ότι η πτώση τάσης στα άκρα της αντίστασης R, δηλαδή IR, ισούται με την διαφορά δυναμικού, q/C, στους οπλισμούς του πυκνωτή. Δηλαδή έχουμε τη σχέση
|
|
(1.25) |
Το ρεύμα του κυκλώματος είναι ίσο με τον ρυθμό μείωσης του
φορτίου στους οπλισμούς του πυκνωτή. Με άλλα λόγια ![]() .
Αντικαθιστώντας στην παραπάνω σχέση βρίσκουμε :
.
Αντικαθιστώντας στην παραπάνω σχέση βρίσκουμε :
|
|
(1.26) |
Ολοκληρώνοντας την απλή διαφορική εξίσωση και λαμβάνοντας υπόψη ότι το αρχικό φορτίο του πυκνωτή είναι Q καταλήγουμε :
|
|
(1.27) |
Αν παραγωγίσουμε την προηγούμενη σχέση ως προς τον χρόνο βρίσκουμε ότι η ένταση του ρεύματος σαν συνάρτηση του χρόνου δίνεται από την σχέση
|
|
(1.28) |
Στο Σχήμα 1.7 βλέπουμε
τις γραφικές παραστάσεις της έντασης του ρεύματος και του φορτίου του πυκνωτή
στην περίπτωση της εκφόρτισης του πυκνωτή στο κύκλωμα RC. Βλέπουμε ότι και το φορτίο και η
ένταση του ρεύματος φθίνουν εκθετικά με ρυθμό που εξαρτάται από την σταθερά χρόνου
![]() του κυκλώματος.
του κυκλώματος.
|
Σχήμα 1.7 H χρονική μεταβολή της έντασης Ι του ρεύματος και του φορτίου q στους οπλισμούς του πυκνωτή κατά την εκφόρτιση του πυκνωτή στο κύκλωμα RC. |
1.6. Κυκλώματα RL.
Όταν ένα κύκλωμα περιλαμβάνει ένα κυκλικό αγωγό ή ένα πηνίο τότε έχει αυτεπαγωγή. Είδαμε ότι το φαινόμενο της αυτεπαγωγής ανθίσταται στην μεταβολή της μαγνητικής ροής εμποδίζοντας στην ουσία το ρεύμα να αυξηθεί ή να μειωθεί ακαριαία.
Ας εξετάσουμε λοιπόν ένα κύκλωμα, όπως αυτό του Σχήματος 1.8, που αποτελείται από μία αντίσταση R και ένα πηνίο με συντελεστή αυτεπαγωγής L συνδεδεμένα εν σειρά. Στο κύκλωμα υπάρχει πηγή συνεχούς ρεύματος π.χ. μία μπαταρία, ηλεκτρεγερτικής δύναμης E και παρεμβάλλεται ένας διακόπτης Δ.
Κατά την χρονική στιγμή t=0 κλείνουμε τον διακόπτη και το κύκλωμα διαρρέεται από ρεύμα έντασης Ι. Ταυτόχρονα με την δημιουργία μαγνητικού πεδίου στο πηνίο και την αύξηση της μαγνητικής ροής δημιουργείται ηλεκτρεγερτική δύναμη λόγω αυτεπαγωγής στα άκρα του πηνίου (βλέπε και §1.4)
|
|
(1.29) |
Η επαγόμενη ηλεκτρεγερτική δύναμη είναι αρνητική μιας και το ρεύμα αυξάνεται. Αυτή η αρνητική ηλεκτρεγερτική δύναμη ανθίσταται στην ηλεκτρεγερτική δύναμη της μπαταρίας και στην περίπτωση αυτή ο δεύτερος κανόνας του Kirchhoff μας δίνει:
Διαιρούμε την εξίσωση με το R και βρίσκουμε
Αν στην προηγούμενη σχέση θέσουμε ![]() , οπότε
, οπότε ![]() η σχέση γίνεται
η σχέση γίνεται
|
|
(1.32) |
Η λύση της εξίσωσης (1.31) είναι
Αντικαθιστώντας ξανά ![]() και παρατηρώντας ότι όταν t=0 τότε Ι=0 και
και παρατηρώντας ότι όταν t=0 τότε Ι=0 και ![]() βρίσκουμε
βρίσκουμε
|
|
(1.34) |
Η εξίσωση (1.33) αποτελεί λοιπόν την λύση της (1.30). Ορίζοντας ως σταθερά χρόνου τ του κυκλώματος τον λόγο R/L, μπορούμε να ξαναγράψουμε την προηγούμενη εξίσωση με την μορφή
|
|
(1.35) |
Ας τροποποιήσουμε λίγο το κύκλωμα του Σχήματος 1.8 αλλάζοντας τον διακόπτη με ένα διακόπτη δύο θέσεων και τοποθετώντας στην θέση 2 του διακόπτη ένα μικρό τμήμα αγωγού που παρακάμπτει την μπαταρία. Το νέο κύκλωμα φαίνεται στο Σχήμα 1.9. Όπως βλέπουμε και από το σχήμα όταν ο διακόπτης είναι στην θέση 1 το κύκλωμα τροφοδοτείται κανονικά από την μπαταρία και ισχύουν όσα αναφέραμε προηγουμένως.
Τοποθετούμε λοιπόν αρχικά τον διακόπτη στη θέση 1 και τον αφήνουμε στη θέση αυτή αρκετή ώρα έτσι ώστε στο κύκλωμα το ρεύμα να αποκτήσει την ασυμπτωτική του τιμή
![]() .
.
Κατόπιν, στην χρονική στιγμή t=0 τοποθετούμε τον διακόπτη στην θέση 2, αφαιρώντας ουσιαστικά από το κύκλωμα την μπαταρία. Στην περίπτωση αυτή έχουμε ε = 0 και από τον κανόνα του Kirchhoff βρίσκουμε
Η διαφορική εξίσωση (1.36) είναι της ίδιας μορφής με την εξίσωση (1.18) οπότε η λύση της είναι ανάλογη της (1.20) δηλαδή
|
|
(1.37) |
όπου τ = L/R η σταθερά χρόνου του κυκλώματος.
Ας πάρουμε ξανά την εξίσωση (1.30) και ας την γράψουμε με την μορφή
Πολλαπλασιάζουμε και τα δύο μέλη της εξίσωσης με την ένταση του ρεύματος Ι
Το αριστερό μέρος της εξίσωσης ( ε Ι ) μας δίνει την ισχύ (ενέργεια ανά μονάδα χρόνου) που παρέχει η μπαταρία στο κύκλωμα. Ο πρώτος όρος του δεξιού μέρους της εξίσωσης ( I2 R ) είναι ως γνωστόν η ισχύς του ηλεκτρικού ρεύματος που καταναλώνεται στην αντίσταση με την μορφή θερμότητας. Ο δεύτερος όρος θα είναι φυσικά και αυτός ισχύς και είναι η ισχύς που αποθηκεύεται στο πηνίο. Η σχέση (1.39) δεν είναι τίποτα άλλο από μία έκφραση του νόμου διατήρησης της ενέργειας.
Αν συμβολίσουμε με Επ την ενέργεια που αποθηκεύεται συνολικά στο πηνίο τότε η χρονική παράγωγος της ενέργειας αυτής (δηλαδή ο ρυθμός μεταβολής της) είναι η ισχύς που αποθηκεύεται στο πηνίο, για την οποία αναφερθήκαμε προηγουμένως. Άρα λοιπόν
Η τελευταία σχέση μας δίνει την ενέργεια που αποθηκεύεται στο μαγνητικό πεδίο του πηνίο. Η σχέση αυτής μοιάζει με την σχέση (1.24) που μας δίνει την ενέργεια που αποθηκεύεται στον ηλεκτρικό πεδίο του πυκνωτή στο κύκλωμα RC. Βλέπουμε λοιπόν ότι και στις δύο περιπτώσεις καταναλώνεται μέρος της ενέργειας της πηγής ηλεκτρικού ρεύματος για να σχηματιστεί το αντίστοιχο πεδίο.
1.7. Ταλαντούμενα κυκλώματα LC.
Ας υποθέσουμε τώρα ότι έχουμε ένα κύκλωμα που αποτελείται μόνο από ένα πυκνωτή χωρητικότητας C και ένα πηνίο με συντελεστή αυτεπαγωγής L. Υποθέτουμε επίσης ότι το κύκλωμα έχει μηδενική ωμική αντίσταση. Στο Σχήμα 1.10 παρουσιάζεται ένα κύκλωμα RL. Έστω λοιπόν ότι ο πυκνωτής είναι αρχικά φορτισμένος με φορτίο Q και την στιγμή t=0 κλείνουμε τον διακόπτη. Ο πυκνωτής εκφορτίζεται και ρεύμα έντασης Ι διαρρέει το κύκλωμα. Το ρεύμα διερχόμενο από το πηνίο δημιουργεί όπως ξέρουμε μαγνητικό πεδίο.
Σε κάθε χρονική στιγμή η ενέργεια που είναι το κύκλωμα διαμοιράζεται στην ενέργεια που είναι αποθηκευμένη στο ηλεκτρικό πεδίο του πυκνωτή και στην ενέργεια που είναι αποθηκευμένη στο μαγνητικό πεδίο του πηνίου. Επειδή το κύκλωμα δεν περιέχει αντίσταση δεν υπάρχουν απώλειες της ηλεκτρικής ενέργειας, η ολική ενέργεια που είναι το άθροισμα της ενέργειας του πηνίου και της ενέργειας του πυκνωτή διατηρείται. Άρα η ολική ενέργεια είναι ίση με την ενέργεια που είχε αρχικά ο πυκνωτής. Αν συμβολίσουμε με E την ολική ενέργεια και με ΕC και ΕL την ενέργεια του πυκνωτή και του πηνίου αντίστοιχα τότε, χρησιμοποιώντας και τις σχέσεις (1.24) και (1.40), έχουμε
Αν παραγωγήσουμε την προηγούμενη σχέση ως προς τον χρόνο βρίσκουμε
μια και τα L και C είναι σταθερές, ενώ μόνο τα q και Ι μεταβάλλονται με τον χρόνο. Έτσι καταλήγουμε στην διαφορική εξίσωση
Ξέρουμε όμως ότι
και επομένως
Αντικαθιστούμε τα ![]() και
και ![]() από τις προηγούμενες σχέσεις στην (1.43) και βρίσκουμε
από τις προηγούμενες σχέσεις στην (1.43) και βρίσκουμε
απλοποιώντας το Ι και από τα δύο μέλη καταλήγουμε στην διαφορική εξίσωση δευτέρας τάξης
Η επίλυση της παραπάνω διαφορικής εξίσωσης είναι απλή. Ιδιαίτερα αν παρατηρήσουμε ότι μοιάζει με την διαφορική εξίσωση, στην μηχανική, της αρμονικής ταλάντωσης που εκτελεί ένα σύστημα μάζας-ελατηρίου.
|
|
(1.48) |
Η οποία έχει λύση της μορφής x=A sin(ωt + β). Η λύση της λοιπόν είναι μία αρμονική ταλάντωση της μορφής
όπου α και β σταθερές τις οποίες θα προσπαθήσουμε να προσδιορίσουμε στην συνέχεια και ω η κυκλική συχνότητα που είναι ίση με
Παραγωγίζοντας την σχέση (1.49) ως προς τον χρόνο βρίσκουμε την σχέση μεταβολής της έντασης του ρεύματος
Ας προσπαθήσουμε τώρα να υπολογίσουμε τις δύο σταθερές α και β στις εξισώσεις (1.49) και (1.51). Την χρονική στιγμή t=0 το φορτίο στον πυκνωτή έχει την μέγιστη τιμή του q=Q ενώ η ένταση ρεύμα είναι μηδέν. Θέτοντας Ι=0 και t=0 στην σχέση (1.51) βρίσκουμε ότι θα πρέπει
|
|
(1.52) |
Επιστρέφοντας στην σχέση (1.49) και θέτοντας q=Q και β=0 βρίσκουμε ότι α=Q οπότε τελικά οι δύο σχέσεις γράφονται
όπου Ιmax=ωQ είναι η μέγιστη ένταση του ρεύματος. Βλέπουμε λοιπόν ότι το φορτίο q ταλαντώνεται (αρμονική ή ημιτονοειδής ταλάντωση) μεταξύ των τιμών -Q και Q, ενώ η ένταση του ρεύματος μεταξύ των -Ιmax και Ιmax με μια διαφορά φάσης 90°. Δηλαδή, όταν το φορτίο μηδενίζεται το ρεύμα γίνεται μέγιστο (κατ’ απόλυτη τιμή) και αντιστρόφως. Στο Σχήμα 1.11 φαίνονται οι χρονικές μεταβολές του φορτίου και της έντασης του ρεύματος.
Ας ξαναγυρίσουμε στην εξίσωση της ενέργειας (1.41) και ας αντικαταστήσουμε το φορτίο και την ένταση του ρεύματος από τις δύο προηγούμενες εξισώσεις.
Βλέπουμε λοιπόν πως η ενέργεια του κυκλώματος ταλαντώνεται
συνεχώς ανάμεσα στην ενέργεια του ηλεκτρικού πεδίου του πυκνωτή (πρώτος όρος
του δεξιού μέρους της εξίσωσης) και του μαγνητικού πεδίου του πηνίου (δεύτερος
όρος του δεξιού μέρους της εξίσωσης). Στο Σχήμα 1.12
παρουσιάζεται γραφικά αυτή η μεταβολή της ενέργειας από ηλεκτρική σε μαγνητική
και αντίστροφα. Το άθροισμα και των δύο, δηλαδή η ολική ενέργεια Ε, είναι πάντα
σταθερό. Υπενθυμίζεται ότι η ολική ενέργεια παραμένει σταθερή μόνο αν
υποθέσουμε ότι το κύκλωμα δεν έχει ωμική αντίσταση. Στην πραγματικότητα αυτό
δεν συμβαίνει ποτέ. Το κύκλωμα πάντα έχει μία έστω και μικρή αντίσταση και έτσι
υπάρχουν απώλειες της ολικής ενέργειας λόγω μετατροπής
|
Σχήμα 1.11 Μεταβολή του φορτίου q του πυκνωτή και της έντασης του ρεύματος I συναρτήσει του χρόνου σε ένα κύκλωμα LC. |
της σε θερμότητα πάνω στην αντίσταση. Επίσης, όπως θα δούμε στην συνέχεια, τα κυκλώματα αυτά εκπέμπουν ηλεκτρομαγνητική ακτινοβολία. Άρα θα έχουμε απώλειες ενέργειας και λόγω αυτής της εκπομπής. Στην ιδανική περίπτωση που εξετάσαμε, όπου δηλαδή υποθέσαμε ότι δεν υπάρχουν απώλειες ενέργειας, οι ταλαντώσεις του κυκλώματος συνεχίζονται έπ’ άπειρον.
Ένα σημείο που ίσως διέφυγε της
προσοχής μας είναι η εξίσωση (1.50). Η εξίσωση αυτή μας
δίνει την κυκλική συχνότητα της ταλάντωσης. Γνωρίζουμε όμως ότι η κυκλική
συχνότητα ω σχετίζεται με την συχνότητα f της ταλάντωσης με την σχέση ω = 2πf. Άρα λοιπόν το κύκλωμα ταλαντώνεται
με συχνότητα
|
Σχήμα 1.12 Χρονική μεταβολή της ενέργειας του μαγνητικού πεδίου του πηνίου EL και του ηλεκτρικού πεδίου του πυκνωτή EC σε κύκλωμα LC. |
Βλέπουμε δηλαδή ότι η συχνότητα ταλάντωσης εξαρτάται μόνο από τα χαρακτηριστικά του κυκλώματος, δηλαδή την χωρητικότητα του πυκνωτή και τον συντελεστή αυτεπαγωγής του πηνίου και όχι από το αρχικό φορτίο του πυκνωτή. Μάλιστα, η συχνότητα είναι αντιστρόφως ανάλογη των χαρακτηριστικών αυτών. Έτσι χρησιμοποιώντας μικρούς πυκνωτές και πηνία μπορούμε να πετύχουμε πολύ μεγάλες συχνότητες ταλάντωσης. Για παράδειγμα, με πυκνωτές μερικών pF και πηνία με συντελεστή αυτεπαγωγής της τάξης των mH, η συχνότητα είναι της τάξης των GHz.
1.8. Κυκλώματα RLC
Στην προηγούμενη παράγραφο υποθέσαμε ότι η ωμική αντίσταση του κυκλώματος είναι μηδέν. Θα εξετάσουμε τώρα την πιο ρεαλιστική περίπτωση
στην οποία το κύκλωμα πέραν του πυκνωτή C και του πηνίου L περιλαμβάνει και ωμική αντίσταση R. Στο Σχήμα 1.13 φαίνεται ένα κύκλωμα αυτού του είδους ή όπως ονομάζεται κύκλωμα RLC.
Ας υποθέσουμε ότι πριν κλείσει ο διακόπτης, ο πυκνωτής είχε φορτίο Q. Με το κλείσιμο του διακόπτη την χρονική στιγμή t=0 το κύκλωμα διαρρέεται από ρεύμα και η ενέργεια που ήταν αποθηκευμένη στον πυκνωτή διαδίδεται στο κύκλωμα και ένα μέρος της αποθηκεύεται στο μαγνητικό πεδίο του πηνίου, ενώ ένα άλλο μέρος της καταναλώνεται με την μορφή θερμότητας πάνω στην αντίσταση.
Στην περίπτωση λοιπόν αυτή στην ολική ενέργεια του συστήματος θα πρέπει εκτός της ενέργειας του ηλεκτρικού πεδίου του πυκνωτή και της ενέργειας του μαγνητικού πεδίου του πηνίου να συμπεριλάβουμε και την ηλεκτρική ενέργεια που μετατρέπεται σε θερμική πάνω στην ωμική αντίσταση. Η ολική ενέργεια του συστήματος, συμπεριλαμβανομένης δηλαδή και της θερμικής, διατηρείται, αλλά η ενέργεια που διαρρέει το κύκλωμα μειώνεται λόγω αυτής της μετατροπής σε θερμότητα σε κάθε χρονική στιγμή με ρυθμό
Έτσι η εξίσωση διατήρησης της ενέργειας (1.43) που είχαμε στο κύκλωμα LC γράφεται στην περίπτωση του κυκλώματος RLC ως
Θέτοντας
|
|
|
βρίσκουμε
και τελικά καταλήγουμε στην διαφορική εξίσωση
Η πλήρης λύση της (1.60) είναι αρκετά πολύπλοκη και ξεφεύγει από τους σκοπούς αυτού του συγγράμματος. Μοιάζει πάντως με την λύση που έχουμε στην μηχανική στην περίπτωση ταλάντωσης με απόσβεση που είναι ανάλογη της ταχύτητας κίνησης π.χ. ταλάντωση μέσα σε υγρό.
Αν υποθέσουμε ότι η αντίσταση R είναι σχετικά μικρή. Η λύση της (1.60) για την περίπτωση αυτή είναι
όπου η κυκλική συχνότητα ω, στην περίπτωση αυτή, δίνεται από την σχέση
|
Σχήμα 1.14 Η μεταβολή του φορτίου q σαν συνάρτηση του χρόνου σε ένα κύκλωμα RLC με μικρή ωμική αντίσταση R, δηλαδή με μικρή απόσβεση. |
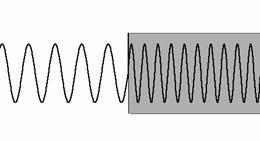
Στο Σχήμα 1.14 παρουσιάζεται η μεταβολή του φορτίου, σύμφωνα με την εξίσωση (1.61) στην περίπτωση που η ωμική αντίσταση είναι σχετικά μικρή έτσι ώστε να έχουμε μικρή απόσβεση. Βλέπουμε δηλαδή ότι το φορτίο εκτελεί μία φθίνουσα ταλάντωση.
Πόσο μικρή όμως πρέπει να είναι η αντίσταση R και τι συμβαίνει αν είναι μεγαλύτερη; Ας δούμε λίγο την σχέση (1.62). Η γωνιακή συχνότητα πρέπει να είναι ένας πραγματικός αριθμός. Για να συμβαίνει όμως αυτό θα πρέπει η ποσότητα που βρίσκεται στα δεξιά της (1.62) μέσα στην ρίζα να είναι ένας θετικός αριθμός ή στην χειρότερη περίπτωση να είναι ίση με μηδέν. Δηλαδή θα πρέπει
|
|
(1.63) |
Θα πρέπει δηλαδή να είναι
|
Σχήμα 1.15 Μεταβολή του φορτίου σε κύκλωμα RLC όταν η ωμική αντίσταση είναι μεγαλύτερη
της κρίσιμης τιμής, |
Η τιμή Rc της αντίστασης ονομάζεται κρίσιμη αντίσταση. Για τιμές της αντίστασης μεγαλύτερες από την Rc η απόσβεση είναι τόσο γρήγορη έτσι ώστε να μην υπάρχει ταλάντωση. Μια τέτοια περίπτωση φαίνεται στο Σχήμα 1.15
Όπως είδαμε λοιπόν από την σχέση (1.61) αλλά και από το Σχήμα 1.14, ακόμη και για πολύ μικρή αντίσταση η ταλάντωση είναι φθίνουσα. Το κύκλωμα δηλαδή μετά από κάποιο χρονικό διάστημα θα σταματήσει πρακτικά να τα ταλαντώνεται. Για να επιτύχουμε η ταλάντωση να συνεχίζεται επ΄ άπειρον θα πρέπει με κάποιο τρόπο να αναπληρώνουμε την ενέργεια που χάνεται με την μορφή θερμότητας πάνω στην ωμική αντίσταση.
Ένα κύκλωμα με το οποίο μπορούμε να επιτύχουμε αμείωτες ταλαντώσεις στον βρόγχο RLC, με αναπλήρωση της ενέργειας, φαίνεται στο Σχήμα 1.16. Το πηνίο L΄ είναι επαγωγικά συζευγμένο με το πηνίο L. Αυξομειώσεις, δηλαδή, της έντασης του ρεύματος που διέρχεται από το πηνίο L και που προκαλούν αυξομειώσεις στο μαγνητικό πεδίο του L, έχουν σαν συνέπεια την δημιουργία ηλεκτρεγερτικής δύναμης στα άκρα του πηνίου L΄ λόγω αμοιβαίας επαγωγής. Το πηνίο L΄ ονομάζεται συνήθως πηνίο ανάδρασης. Το πηνίο ανάδρασης συνδέεται με την βάση και τον εκπομπό ενός τρανζίστορ (κρυσταλοτρίοδος) μεταβάλλοντας την μεταξύ των δύο ακροδεκτών διαφορά δυναμικού που με την σειρά της μεταβάλει την ένταση του ρεύματος στο κύκλωμα αναπλήρωσης ενέργειας. Έτσι με τον ίδιο ρυθμό με τις ταλαντώσεις του κυκλώματος RLC το κύκλωμα αναπλήρωσης δίνει ρυθμικές ενισχύσεις στο ρεύμα του κυκλώματος RLC. H λειτουργία, λοιπόν, του κυκλώματος αυτού, είναι παρόμοια με το παιδί που κάνει κούνια και τον παππού (ή τη γιαγιά) που με τον ίδιο ρυθμό με την κούνια σπρώχνουν περιοδικά, έτσι ώστε να αναπληρώνεται η ενέργεια που χάνεται από τις τριβές και την αντίσταση του αέρα.
2. Ηλεκτρομαγνητικά κύματα
2.1. Εισαγωγή
Με τον όρο “κύματα” συνήθως εννοούμε τα κύματα που διαδίδονται μέσα στην ύλη όπως για παράδειγμα τα κύματα της θάλασσας, τα κύματα στις τεντωμένες χορδές ενός πιάνου, τα ηχητικά κύματα κ.λ.π. Τα κύματα αυτά συνήθως ονομάζονται μηχανικά κύματα μιας και ουσιαστικά είναι μηχανικές παραμορφώσεις της ύλης μέσα στην οποία διαδίδονται.
Στο κεφάλαιο αυτό θα ασχοληθούμε με τα ηλεκτρομαγνητικά κύματα που αποτελούν παραμορφώσεις του ηλεκτρικού και μαγνητικού πεδίου και που φυσικά, εφόσον δεν έχουν ανάγκη της ύλης για να διαδοθούν, διαδίδονται και στο κενό.
Ξεκινώντας από τις θεωρία του Maxwell που προέβλεψε την ύπαρξη και διάδοση των ηλεκτρομαγνητικών κυμάτων θα εξετάσουμε τους τρόπους δημιουργίας των. Θα δούμε πως και το φως ή καλύτερα η φωτεινή ακτινοβολία είναι και αυτή ηλεκτρομαγνητικά κύματα και θα γνωρίσουμε το φάσμα των ηλεκτρομαγνητικών κυμάτων. Τέλος θα εξετάσουμε πως τα ηλεκτρομαγνητικά κύματα διαδίδονται στον χώρο.
2.2. Η θεωρία του Maxwell
O Maxwell, ίσως ο μεγαλύτερος θεωρητικός φυσικός του 19ου αιώνα, συνδυάζοντας τις τότε γνωστές θεωρίες για τον ηλεκτρισμό και τον μαγνητισμό πρότεινε μια ενιαία θεωρία, την θεωρία του ηλεκτρομαγνητισμού, δίνοντας εξήγηση σε όλα τα μέχρι τότε γνωστά προβλήματα αυτού του τομέα της φυσικής. Αλλά η αξία της θεωρίας του δεν περιορίστηκε μόνο στην ερμηνεία των μέχρι τότε γνωστών φαινομένων. Προέβλεπε πριν ακόμη ανακαλυφθούν και την ύπαρξη των ηλεκτρομαγνητικών κυμάτων. Τα ηλεκτρομαγνητικά κύματα παρήχθησαν και ανιχνεύθηκαν για πρώτη φορά το 1887 από τον Hertz, οκτώ χρόνια μετά τον θάνατο του Maxwell.
Η ηλεκτρομαγνητική θεωρία περιγράφεται πλήρως από ένα σύνολο τεσσάρων εξισώσεων που έχουν γίνει πια γνωστές σαν εξισώσεις του Maxwell, παρόλο που κάθε μία από αυτές έχει προταθεί από διαφορετικούς επιστήμονες. Οι τέσσερις αυτές εξισώσεις είναι
|
|
(2.1) |
|
|
(2.2) |
H πρώτη εξίσωση, γνωστή και σαν νόμος του Gauss, μας λέει ότι “H ολική ροή του ηλεκτρικού πεδίου, που περνάει μέσα από μία κλειστή επιφάνεια S, ισούται με το ολικό φορτίο Q, που περιέχεται μέσα στην επιφάνεια, προς την ηλεκτρική διαπερατότητα του κενού ε0”.
Η δεύτερη εξίσωση αναφέρεται και ως νόμος του Gauss για τον μαγνητισμό και ορίζει ότι “η ολική ροή του μαγνητικού πεδίου που διέρχεται μέσα από μία κλειστή επιφάνεια είναι ίση με το μηδέν”.
H τρίτη εξίσωση, είναι ο νόμος της επαγωγής του Faraday. O νόμος ορίζει ότι “το επικαμπύλιο ολοκλήρωμα της έντασης του ηλεκτρικού πεδίου Ε που υπολογίζεται κατά μήκος μιας κλειστής καμπύλης L, ισούται με τον ρυθμό μεταβολής της μαγνητικής ροής που περνά από την επιφάνεια που περικλείεται από την κλειστή καμπύλη”. Η σχέση (2.3) ίσως φαίνεται διαφορετική από την σχέση του νόμου του Faraday όπως αυτή αναφέρθηκε στο Κεφάλαιο 1, δηλαδή την σχέση (1.12), αλλά στην ουσία είναι ίδια, αφού το επικαμπύλιο ολοκλήρωμα δεν είναι τίποτε άλλο από την ηλεκτρεγερτική δύναμη που εμφανίζεται στα άκρα ενός αγωγού που έχει το σχήμα της καμπύλης L.
Τέλος, η τέταρτη εξίσωση είναι ο νόμος του Ampére έτσι όπως γενικεύτηκε από τον Maxwell, για τον λόγο αυτό αναφέρεται και ως νόμος των Ampére - Maxwell. Η εξίσωση ορίζει ότι “το επικαμπύλιο ολοκλήρωμα του μαγνητικού πεδίου (μαγνητικής επαγωγής) κατά μήκος μιας κλειστής καμπύλης είναι ανάλογο (με σταθερή αναλογίας μ0) με το άθροισμα του ρεύματος αγωγιμότητας Ι που περνά μέσα από μία επιφάνεια της οποίας το όριο είναι η κλειστή καμπύλη, συν το ρεύμα μετατόπισης (ε0 dΦe/dt).
Οι τέσσερις αυτές εξισώσεις ενοποιούν πλήρως τον ηλεκτρισμό με τον μαγνητισμό λέγοντας ουσιαστικά ότι είναι οι δύο όψεις το ιδίου νομίσματος, του ηλεκτρομαγνητισμού. Παρατηρώντας μάλιστα τις δύο τελευταίες εξισώσεις βλέπουμε ότι ένα μεταβαλλόμενο ηλεκτρικό πεδίου παράγει μαγνητικό πεδίο που με την σειρά του όταν μεταβάλλεται παράγει ηλεκτρικό πεδίο (και αντίστροφα).
2.3. Ηλεκτρομαγνητικά κύματα
Από τις εξισώσεις (2.3) και (2.4) μπορούμε, μετά από μερικές μάλλον επίπονες πράξεις, να αποδείξουμε την ύπαρξη και να βρούμε τις ιδιότητες των ηλεκτρομαγνητικών κυμάτων. Η αυστηρά όμως μαθηματική απόδειξη ξεφεύγει από τα πλαίσια του συγγράμματος και τους σκοπούς διδασκαλίας του μαθήματος στο Τμήμα Πληροφορικής και Επικοινωνιών. Για τον λόγο αυτό θα ακολουθήσουμε έναν κάπως πιο εύκολο και όχι τόσο μαθηματικό τρόπο για να εξαγάγουμε από τις δύο τελευταίες εξισώσεις του Maxwell την εξίσωση των ηλεκτρομαγνητικών κυμάτων.
Ας υποθέσουμε λοιπόν ότι έχουμε ένα επίπεδο ηλεκτρομαγνητικό κύμα το οποίο οδεύει με μία ταχύτητα υ προς τον άξονα x. Το κύμα έχει το διάνυσμα της έντασης Ε του ηλεκτρικού πεδίου να ταλαντώνεται κατά μήκος της διεύθυνσης y και το διάνυσμα της μαγνητικής επαγωγής B να ταλαντώνεται κατά την διεύθυνση του άξονα z. Στο Σχήμα 2.1 παρουσιάζεται η μορφή ενός τέτοιου κύματος. Τέτοιου είδους κύματα που τα E και B ταλαντώνονται μόνο κατά μήκος ορισμένων διευθύνσεων ονομάζονται, όπως θα δούμε και σε επόμενο κεφάλαιο, γραμμικώς πολωμένα.
|
Σχήμα 2.1 Γραφική αναπαράσταση ενός ηλεκτρομαγνητικού κύματος που διαδίδεται κατά την θετική διεύθυνση του άξονα x. |
Υποθέτοντας ότι το κύμα διαδίδεται στο κενό, όπου δεν υπάρχουν φορτία και ηλεκτρικό ρεύμα (Q=0 και Ι=0), οι δύο τελευταίες εξισώσεις του Maxwell γράφονται
Μιας και το κύμα είναι επίπεδο και το Ε έχει συνιστώσα μόνο κατά την διεύθυνση y ενώ το B μόνο κατά την z καταλήγουμε στις ακόλουθες διαφορικές εξισώσεις.
|
|
(2.8) |
Παραγωγίζοντας την (2.5) έχουμε και χρησιμοποιώντας την (2.6)
|
|
(2.9) |
από την οποία καταλήγουμε στην
Όμοια παραγωγίζοντας την (2.6) καταλήγουμε στην σχέση
Οι εξισώσεις (2.10) και (2.11) έχουν την γενική μορφή της εξίσωσης κύματος
|
|
|
που διαδίδεται κατά την διεύθυνση x με ταχύτητα υ. Άρα λοιπόν οι εξισώσεις (2.10) και (2.11) παριστάνουν ένα ηλεκτρομαγνητικό που διαδίδεται με ταχύτητα ίση με
|
|
(2.12) |
Χρησιμοποιώντας τις γνωστές τιμές για τις σταθερές μ0 = 4π 10-7 Wb/A m και ε0 = 8.8542 10-12 C2/N m2 βρίσκουμε ότι η ταχύτητα διάδοσης των ηλεκτρομαγνητικών κυμάτων στο κενό είναι
υ = 2.99792 108 m/s
Η ταχύτητα όμως αυτή είναι ίδια με την ταχύτητα του φωτός στο κενό c. Άρα λοιπόν τα ηλεκτρομαγνητικά κύματα διαδίδονται με την ταχύτητα του φωτός.
Τα ηλεκτρομαγνητικά κύματα λοιπόν έχουν μία συχνότητα f και ένα μήκος κύματος λ που σχετίζονται με την απλή σχέση
|
|
(2.13) |
Η πιο απλή εξίσωση κύματος, λύση των εξισώσεων (2.10) και (2.11) είναι
όπου η σταθερή k ονομάζεται κυματάριθμος και είναι ίση με k = 2π / λ, ενώ η γωνιακή ταχύτητα ω είναι ίση με ω=2π f.
Αν παραγωγίσουμε τις εξισώσεις (2.14) και (2.15), την πρώτη ως προς x και την δεύτερη ως προς t, έχουμε
|
|
(2.16) |
|
|
(2.17) |
Συνδυάζοντας τις παραπάνω εξισώσεις με την (2.7) καταλήγουμε
|
|
(2.18) |
Εφόσον ο λόγος των μέγιστων τιμών του ηλεκτρικού και του μαγνητικού πεδίου είναι σταθερός τότε, σύμφωνα με τις σχέσεις (2.14) και (2.15), θα έχουμε πάντα
Η ένταση, δηλαδή, του ηλεκτρικού πεδίου και η ένταση (μαγνητική επαγωγή) του μαγνητικού πεδίου σε ένα ηλεκτρομαγνητικό κύμα μεταβάλλονται έτσι ώστε σε κάθε σημείο του χώρου που το κύμα διαδίδεται και σε κάθε χρονική στιγμή, λόγος τους να είναι ίσος με την ταχύτητα του φωτός.
2.4. Το φως είναι ηλεκτρομαγνητικό κύμα
Στο δεύτερο μισό του 19ου αιώνα, πρώτος ο Maxwell θεωρητικά και στην συνέχεια ο Hertz και άλλοι ερευνητές πειραματικά εξέτασαν τις ιδιότητες των ηλεκτρομαγνητικών κυμάτων. Έτσι βρήκαν ότι τα ηλεκτρομαγνητικά κύματα:
· ανακλώνται από μεταλλικές επιφάνειες όπως το φως
· διαθλώνται όταν διέρχονται από διηλεκτρικά με τους ίδιους νόμους με αυτούς που ισχύουν για το φως
· παράγουν φαινόμενα συμβολής και περίθλασης όπως και στην περίπτωση του φωτός
και σαν να μην έφταναν όλες οι παραπάνω ιδιότητες που είναι όμοιες με αυτές του φωτός, ο Maxwell απέδειξε ότι τα ηλεκτρομαγνητικά κύματα διαδίδονται με την ταχύτητα του φωτός.
Όλα αυτά οδήγησαν στο συμπέρασμα ότι τα ηλεκτρομαγνητικά κύματα είναι φως… ή μάλλον καλύτερα, ότι το φως είναι και αυτό ένα ηλεκτρομαγνητικό κύμα. Έτσι, ουσιαστικά, ο Maxwell δεν ενοποίησε απλώς τον ηλεκτρισμό με τον μαγνητισμό αλλά ενσωμάτωσε και την οπτική μέσα στην ενιαία ηλεκτρομαγνητική θεωρία.
2.5. Δημιουργία και εκπομπή ηλεκτρομαγνητικών κυμάτων
Εξετάζοντας τις δύο τελευταίες εξισώσεις του Maxwell βλέπουμε ότι ηλεκτρομαγνητικά κύματα δημιουργούνται από
· Μεταβαλλόμενα μαγνητικά πεδία τα οποία δημιουργούν ηλεκτρικά πεδία
· Μεταβαλλόμενα ηλεκτρικά πεδία τα οποία δημιουργούν μαγνητικά πεδία
Πιο γενικά θα μπορούσαμε να πούμε ότι “Η επιτάχυνση των ηλεκτρικών φορτίων είναι το αίτιο που δημιουργεί την ηλεκτρομαγνητική ακτινοβολία. Όταν φορτισμένο σωμάτιο π.χ. ένα ηλεκτρόνιο, επιταχύνεται ή επιβραδύνεται, εκπέμπει ηλεκτρομαγνητική ακτινοβολία.”
Ας εξετάσουμε πρώτα την παραγωγή ηλεκτρομαγνητικών κυμάτων από ένα ηλεκτρικό δίπολο ή όπως συνήθως ονομάζεται μία διπολική κεραία. Η κεραία αποτελείται από δύο μεταλλικές ράβδους στις οποίες συνδέουμε με κύκλωμα παροχής εναλλασσόμενης τάσης. Στο Σχήμα 2.2 παρουσιάζεται μία τέτοια κεραία. Η παρεχόμενη εναλλασσόμενη τάση μεταβάλλεται ημιτονοειδώς με τον χρόνο με μία συχνότητα ν.
|
|
(2.20) |
Στην χρονική στιγμή t=0 η παρεχόμενη τάση είναι μηδέν και
η κεραία δεν παρουσιάζει φορτία. Καθώς ο χρόνος περνάει η τάση γίνεται θετική με
τιμή που συνεχώς αυξάνει και την χρονική στιγμή t=T/4 η τάση γίνεται μέγιστη. Ταυτόχρονα
με την αύξηση της τάσεις το ένα άκρο (η μία ράβδος) της κεραίας φορτίζεται
θετικά ενώ το άλλο άκρο της κεραίας αρνητικά. Εμφανίζεται έτσι ηλεκτρικό πεδίο
το οποίο αυξάνεται μέχρι την στιγμή t=T/4. Στην συνέχεια και μέχρι την
χρονική στιγμή Τ/2 η τάση της πηγής μειώνεται παραμένοντας όμως θετική, κατά
συνέπεια μειώνονται και τα φορτία στις δύο ράβδους. Το ηλεκτρικό πεδίο αρχίζει
και αυτό να μειώνεται μέχρις ότου μηδενιστεί στην χρονική στιγμή Τ/2. Στην
συνέχεια αρχίζει ο αντίστροφος (αρνητικός) κύκλος όπου η τάση γίνεται αρνητική
και οι δύο ράβδοι φορτίζονται με αντίθετα (σε σχέση με τον θετικό) φορτία. Το
ηλεκτρικό πεδίο που δημιουργείται γύρω από το δίπολο κάθε στιγμή διαδίδεται
στον χώρο με την ταχύτητα του φωτός c. Έτσι την χρονική στιγμή t=T το ηλεκτρικό πεδίο δίπλα στο δίπολο
έχει τιμή μηδέν, ενώ σε απόσταση c·T/4 από το δίπολο το ηλεκτρικό πεδίο παίρνει την
μέγιστη του τιμή, όπως δηλαδή ήταν το πεδίο δίπλα στο δίπολο πριν από χρόνο Τ/4
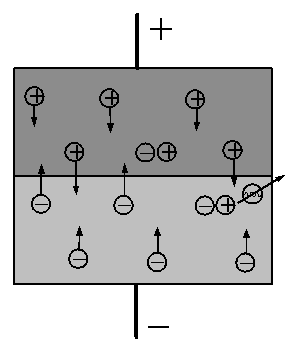
(την στιγμή δηλαδή 3Τ/4). Στο Σχήμα 2.3 βλέπουμε το
ηλεκτρικό πεδίο που δημιουργείται από την κεραία και πώς αυτό διαδίδεται προς
τα δεξιά σε διαφορετικές χρονικές στιγμές.
|
Σχήμα 2.3 Δημιουργία και διάδοση του ηλεκτρικού πεδίου στην διάρκεια μιας περιόδου από μία διπολική κεραία. |
Ταυτόχρονα με το ηλεκτρικό πεδίο παράγεται και μαγνητικό πεδίο που είναι κάθετο στο επίπεδο του Σχήματος 2.2. Την χρονική στιγμή t=0 κατά την οποία αρχίζουν οι δύο ράβδοι του διπόλου να φορτίζονται το ρεύμα που διαρρέει το δίπολο είναι μέγιστο με αποτέλεσμα το δημιουργούμενο μαγνητικό πεδίο να παίρνει την μέγιστη τιμή. Όταν η τάση λαμβάνει την μέγιστη τιμή και το ηλεκτρικό πεδίο γίνεται μέγιστο, το ρεύμα που διαρρέει το δίπολο μηδενίζεται με συνέπεια να μηδενιστεί και το μαγνητικό πεδίο. Στην συνέχεια η τάση μειώνεται με αποτέλεσμα να έχουμε μετακίνηση φορτίων κατά την αντίθετη φορά. Το μαγνητικό πεδίο ξαναρχίζει να αυξάνεται με φορά όμως αντίθετη από την προηγούμενη.
Έτσι λοιπόν έχουμε μία ημιτονοειδώς περιοδική μεταβολή των δύο πεδίων η οποία όπως προαναφέραμε διαδίδεται στον χώρο με ταχύτητα c. Ας σημειωθεί ότι το ηλεκτρικό πεδίο και το μαγνητικό πεδίο κοντά στην κεραία έχουν διαφορά φάσης 90°. Δηλαδή όταν το ένα μηδενίζεται το άλλο παίρνει την μέγιστη (θετική ή αρνητική) τιμή του και αντίστροφα.
Στο προηγούμενο κεφάλαιο εξετάσαμε τα
κυκλώματα LC και RLC στα οποία η ενέργεια μεταφέρεται περιοδικά από το ηλεκτρικό πεδίο του
πυκνωτή στο μαγνητικό πεδίο του πηνίου. Είδαμε ότι μπορούμε να επιτύχουμε
ταλαντώσεις πολύ μεγάλης συχνότητας χρησιμοποιώντας πυκνωτές πολύ μικρής
χωρητικότητας και πηνία πολύ μικρού συντελεστή αυτεπαγωγής.
|
Σχήμα 2.4 Μετάβαση από το κλειστό κύκλωμα LC στο ανοικτό κύκλωμα ενός παλλόμενου ηλεκτρικού διπόλου. |
Ας πάρουμε ένα κύκλωμα LC όπως αυτό του Σχήματος 2.4a. Ανάμεσα στους οπλισμούς του πυκνωτή εμφανίζεται όπως γνωρίζουμε ηλεκτρικό πεδίο. Απομακρύνουμε σιγά - σιγά τους οπλισμούς του πυκνωτή και τους φέρουμε σε θέση όπως στο Σχήμα 2.4c. Το ηλεκτρικό πεδίο τώρα διαχέεται στον χώρο. Αν επιπλέον αντικαταστήσουμε το πηνίο με έναν ευθύγραμμο αγωγό (Σχήμα 2.4d) τότε το κύκλωμα που προκύπτει είναι ένα παλλόμενο ηλεκτρικό δίπολο. Το ηλεκτρικό αυτό δίπολο όπως είδαμε προηγουμένως εκπέμπει ηλεκτρομαγνητική ακτινοβολία συχνότητας ίδιας με την συχνότητα ταλάντωσης του διπόλου. Ένα σημείο που θα πρέπει να τονίζουμε είναι ότι με το να ανοίξουμε τον πυκνωτή και να χρησιμοποιήσουμε ευθύγραμμο αγωγό έχουμε μειώσει πολύ την χωρητικότητα C και την αυτεπαγωγή L του κυκλώματος. Έτσι το κύκλωμα πάλλεται πολύ γρήγορα, εκπέμποντας ακτινοβολία πολύ μεγάλης συχνότητας, σύμφωνα με την σχέση (1.56) του προηγούμενου κεφαλαίου.
Εκτός από την διπολική κεραία, ηλεκτρομαγνητικά κύματα, όπως προαναφέραμε, δημιουργούνται όταν έχουμε αλλαγή της κινητικής κατάστασης (με άλλα λόγια επιτάχυνση) των φορτίων. Έτσι αν για παράδειγμα πάρουμε ένα φορτισμένο σώμα και αρχίσουμε να το κουνάμε δεξιά-αριστερά στον αέρα, τότε δημιουργούμε ηλεκτρομαγνητικά κύματα.
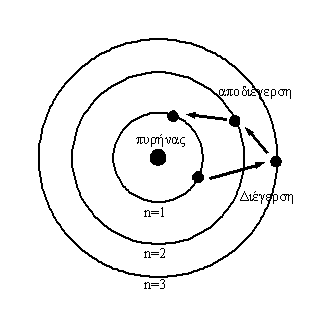
Στα άτομα, γνωρίζουμε από την ατομική φυσική, τα ηλεκτρόνια κατανέμονται σε στοιβάδες γύρω από τον πυρήνα. Σε ορισμένες περιπτώσεις ηλεκτρόνια που βρίσκονται σε ανώτερη στοιβάδα από αυτή που πρέπει να ήταν κανονικά, όταν δηλαδή το άτομο είναι διεγερμένο, μεταπίπτουν πίσω στην βασική τους στοιβάδα. Αυτή η μετάπτωση συνοδεύεται με εκπομπή ηλεκτρομαγνητικής ακτινοβολίας, μιας και το ηλεκτρόνιο, άρα και το φορτίο του, επιταχύνονται και αλλάζουν κινητική κατάσταση έτσι ώστε να μπορέσουν να μετακινηθούν σε κατώτερη στοιβάδα.
2.6. Η ενέργεια των ηλεκτρομαγνητικών κυμάτων
Τα ηλεκτρομαγνητικά κύματα καθώς διαδίδονται στον χώρο μεταφέρουν ενέργεια. Η ενέργεια αυτή ή μάλλον καλύτερα ο ρυθμός ροής της ενέργειας περιγράφεται με το διάνυσμα Poynting που ορίζεται ως
|
|
(2.21) |
και περιγράφει τον ρυθμό ροής της ενέργειας, δηλαδή την ενέργεια
στην μονάδα του χρόνου, με άλλα λόγια την ισχύ, μέσα από μια μοναδιαία
επιφάνεια που είναι κάθετη στην διεύθυνση διάδοσης του κύματος. Η μονάδα
μέτρησης φυσικά είναι W/m2
(ισχύς ανά μονάδα επιφανείας). Η διεύθυνση του διανύσματος S είναι κάθετη στο επίπεδο που ορίζουν
τα διανύσματα ![]() και
και ![]() .
Αν υποθέσουμε ότι το διάνυσμα
.
Αν υποθέσουμε ότι το διάνυσμα ![]() κατευθύνεται
κατά την διεύθυνση του άξονα x και το
κατευθύνεται
κατά την διεύθυνση του άξονα x και το ![]() κατά την
διεύθυνση του άξονα y, τότε το διάνυσμα
κατά την
διεύθυνση του άξονα y, τότε το διάνυσμα ![]() κατευθύνεται προς
την διεύθυνση του άξονα z.
κατευθύνεται προς
την διεύθυνση του άξονα z.
Σ’ ένα επίπεδο ηλεκτρομαγνητικό κύμα τα διανύσματα ![]() και
και
![]() είναι κάθετα μεταξύ τους.
Άρα το διάνυσμα
είναι κάθετα μεταξύ τους.
Άρα το διάνυσμα ![]() έχει μέτρο ίσο με Ε
Β. Έχουμε λοιπόν
έχει μέτρο ίσο με Ε
Β. Έχουμε λοιπόν
|
|
(2.22) |
Αλλά γνωρίζουμε ότι ![]() , άρα
, άρα
|
|
(2.23) |
Αν πάρουμε ένα αρμονικό ηλεκτρομαγνητικό κύμα, ένα κύμα δηλαδή που το ηλεκτρικό και μαγνητικό του πεδίο δίνεται από τις σχέσεις (2.14) και (2.15). Ο μέσος όρος του S κατά την διάρκεια μίας περιόδου ονομάζεται ένταση του κύματος και συμβολίζεται με Ι (προσοχή να μην το συγχέεται με την ένταση του ρεύματος σε έναν αγωγό που επίσης συμβολίζεται με Ι). Η ένταση του κύματος για το αρμονικό ηλεκτρομαγνητικό κύμα είναι ίσο με
|
|
(2.24) |
Τέλος ας ξαναδούμε λίγο την διπολική κεραία και ας εξετάσουμε την διεύθυνση του διανύσματος Poynting. Βλέπουμε και στο Σχήμα 2.5 ότι το διάνυσμα S κατευθύνεται πάντα προς τα έξω παρόλο που τα Ε και Β αλλάζουν φορά. Έτσι έχουμε μια συνεχή εκροή ενέργειας από την διπολική κεραία. Η ενέργεια αυτή πρέπει να συμπληρώνεται από μία ηλεκτρική πηγή.
2.7. Το φάσμα των ηλεκτρομαγνητικών κυμάτων.
Οι ηλεκτρομαγνητικές ακτινοβολίες έχουν ένα πολύ μεγάλο φάσμα, με συχνότητες από μερικές εκατοντάδες Hz μέχρι και 1022 Ηz. Επειδή η συχνότητα και το μήκος κύματος συνδέονται με την απλή σχέση c = f λ, πολλές φορές για να χαρακτηρίσουμε ένα κύμα αντί της συχνότητας χρησιμοποιούμε το μήκος κύματος.
Στο σημείο αυτό θα ήταν χρήσιμο να παραθέσουμε ένα πίνακα με τις μονάδες μέτρησης της συχνότητας και του μήκους κύματος.
|
Συχνότητα |
|
Μήκος κύματος |
||||
|
1 kΗz |
k=kilo |
103 Hz |
|
1 mm |
m=milli |
10-3 m |
|
1 MHz |
M=mega |
106 Hz |
|
1 μm |
μ=micro |
10-6 m |
|
1 GHz |
G=giga |
109 Hz |
|
1 nm |
n=nano |
10-9 m |
|
1 THz |
T=tera |
1012 Hz |
|
1 pm |
p=pico |
10-12 m |
|
|
|
|
1 Å |
ångström |
10-10 m |
|
Στον παρακάτω πίνακα παρουσιάζεται η δομή του φάσματος της ηλεκτρομαγνητικής ακτινοβολίας. Οι διάφορες ονομασίες των διαφορετικών τμημάτων του φάσματος είναι οι συνηθέστερες ονομασίες. Πρέπει να τονιστεί ότι δεν υπάρχουν σαφή όρια μεταξύ των διαφόρων ακτινοβολιών.
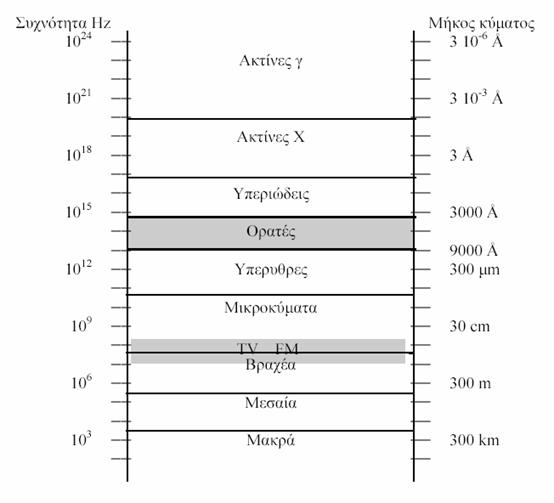
Τα ραδιοκύματα (βραχέα, μεσαία και μακρά) δημιουργούνται από ηλεκτρονικά κυκλώματα π.χ. κυκλώματα LC. Χρησιμοποιούνται συνήθως στις τηλεπικοινωνίες, τηλεόραση και ραδιόφωνο.
Τα μικροκύματα (στα οποία συμπεριλαμβάνονται και μέρος των βραχέων) παράγονται επίσης από ηλεκτρονικά κυκλώματα. Χρησιμοποιούνται σε τηλεπικοινωνίες, ραντάρ κ.λ.π. Μια συνηθισμένη οικιακή εφαρμογή τους είναι για η θέρμανση ή το μαγείρεμα των φαγητών, λόγω της υψηλής απορρόφησης τους από το νερό δηλαδή από την υγρασία που έχουν τα τρόφιμα.
Οι υπέρυθρες ακτίνες εκπέμπονται από τα διάφορα θερμά σώματα και μόρια λόγω των ταλαντώσεων και κινήσεων των μορίων τους. Ας μην ξεχνάμε ότι η θερμοκρασία ενός σώματος είναι ένα μέτρο της κινητικής ενέργειας των μορίων του. Έτσι όσο θερμότερο είναι ένα σώμα τόσο πιο έντονα ακτινοβολεί στο υπέρυθρο. Χρησιμοποιούνται για επιστημονικούς και θεραπευτικούς σκοπούς. Μια κάπως γνωστή εφαρμογή τους είναι τα στρατιωτικά κιάλια υπερύθρων και η κατασκοπευτική υπέρυθρη φωτογραφία που επιτρέπει την φωτογράφηση στόχων στο σκοτάδι.
Οι ορατές ακτίνες είναι οι πιο γνωστές και είναι αυτές που διεγείρουν τον αμφιβληστροειδή χιτώνα του ανθρώπινου οφθαλμού. Χωρίζονται σε χρώματα από το ερυθρό (7000 Ǻ) έως το ιώδες (4000 Ǻ). Παράγονται από την ανακατανομή των ηλεκτρονίων στις διάφορες ηλεκτρονικές στοιβάδες στα άτομα.
Οι υπεριώδεις ακτίνες επίσης παράγονται από την ανακατανομή των ηλεκτρονίων στα άτομα. Το “μαύρισμα” της καλοκαιρινής ηλιοθεραπείας οφείλεται στην αντίδραση της επιδερμίδας μας σ’ αυτές τις ακτινοβολίες. Οι ακτινοβολίες όμως αυτές είναι γενικά βλαβερές για τα κύτταρα. Ο Ήλιος μας εκπέμπει τεράστια ποσά τέτοιας ακτινοβολίας. Ευτυχώς το μεγαλύτερο μέρος της απορροφάται στα ανώτερα στρώματα της ατμόσφαιρας από το λεγόμενο “στρώμα του όζοντος” (Ο3) και μετατρέπεται σε θερμότητα (υπέρυθρη ακτινοβολία).
Οι ακτίνες Χ (ή ακτίνες Röntgen) παράγονται συνήθως από την επιβράδυνση ταχέως κινούμενων ηλεκτρονίων όταν αυτά προσκρούουν πάνω σε ένα μεταλλικό στόχο. Η χρήση τους στην ιατρική, διαγνωστική και θεραπευτική, είναι σε όλους γνωστή. Προσοχή όμως γιατί σε υπερβολική έκθεση μπορεί να βλάψουν ή και να καταστρέψουν τα κύτταρα.
Τέλος οι ακτίνες γ εκπέμπονται από ορισμένους ραδιενεργούς πυρήνες, τις αντιδράσεις πυρήνων με στοιχειώδη σωμάτια, την διάσπαση ορισμένων στοιχειωδών σωματιδίων όπως π.χ. το π-μεσόνιο και τις πυρηνικές αντιδράσεις. Χρησιμοποιούνται στην ιατρική για διαγνωστικούς σκοπούς (ραδιοϊσότοπα, γ-camera). Είναι πολύ διεισδυτικές και βλάπτουν τον οργανισμό. Είναι, δυστυχώς, σε όλους μας γνωστά τα αποτελέσματα της ραδιενέργειας από τις δύο εκρήξεις ατομικών βομβών στην Ιαπωνία κατά την διάρκεια του Β’ Παγκοσμίου Πολέμου.
2.8. Διάδοση της ηλεκτρομαγνητικής ακτινοβολίας
Όπως αναφέραμε και προηγουμένως ηλεκτρομαγνητικά κύματα δημιουργούνται από επιτάχυνση φορτίων και διαδίδονται στον χώρο με την ταχύτητα του φωτός. Ας εξετάσουμε λίγο παραπάνω την διάδοση των ηλεκτρομαγνητικών κυμάτων που παράγονται από ένα ηλεκτρικό δίπολο.
Ας πάρουμε λοιπόν ένα ηλεκτρικό δίπολο που το μήκος του είναι ίσο με το μισό του μήκους κύματος της εκπεμπόμενης από αυτό ηλεκτρομαγνητικής ακτινοβολίας. Ένα τέτοιο δίπολο ονομάζεται κεραία μισού μήκους κύματος ή διπολική κεραία ή κεραία του Hertz.
Στην περιοχή κοντά στην κεραία το ηλεκτρικό και το μαγνητικό πεδίο παρουσιάζουν, όπως είδαμε στην § 2.5 παρουσιάζουν διαφορά φάσης 90°. Επίσης τα δύο πεδία μειώνονται με την απόσταση r από το δίπολο ανάλογα με το 1/r3. Άρα δεν θα έπρεπε να απαντώνται σε μεγάλες αποστάσεις από την κεραία.
Στην πραγματικότητα, λόγω ακριβώς των εξισώσεων του Maxwell, σε μεγάλες αποστάσεις από την κεραία δημιουργείται, δευτερογενώς, ηλεκτρικό πεδίο από επαγωγή λόγω του μεταβαλλόμενου μαγνητικού πεδίου. Το ηλεκτρικό αυτό πεδίο δημιουργεί με την σειρά του μαγνητικό πεδίο. Τα δευτερογενώς δημιουργούμενα πεδία βρίσκονται σε φάση και μειώνονται με ρυθμό ανάλογο του 1/r. Η σε φάση διάδοση των δύο πεδίων έχει σαν αποτέλεσμα την συνεχή εκροή ενέργειας από την κεραία. Το διάνυσμα Poynting και άρα και η ισχύς της ακτινοβολίας μεταβάλλεται με την απόσταση ανάλογα με το 1/r2.
Το πεδίο κοντά στην κεραία συνήθως ονομάζεται κοντινό πεδίο σε αντίθεση με το πεδίο μακριά από την κεραία που συνήθως μακρινό πεδίο. Η διάκριση μεταξύ των δύο πεδίων δεν είναι αυστηρά σαφής. Γενικά θα μπορούσαμε να ορίσουμε πώς το μακρινό πεδίο αρχίζει από μία απόσταση rF που είναι ίση με
|
|
(2.25) |
όπου d το μήκος της κεραίας. Για την περίπτωση μας της διπολικής
κεραίας μισού μήκους κύματος το μακρινό πεδίο αρχίζει από μία απόσταση ίση με
λ/2.
|
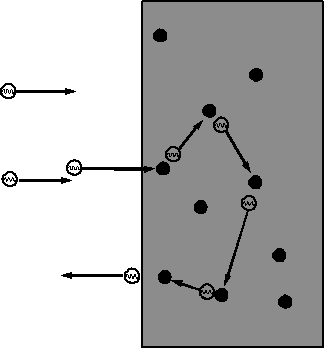
Σχήμα 2.6 Το ηλεκτρικό πεδίο της εκπεμπόμενης, από μία κεραία μισού μήκους κύματος, ηλεκτρομαγνητικής ακτινοβολίας. |
Οι γραμμές του ηλεκτρικού πεδίου που δημιουργούνται από την διπολική κεραία μισού μήκους κύματος παρουσιάζονται στο Σχήμα 2.6. Η μέγιστη ισχύς εκπέμπεται κατά μήκος της ευθείας που είναι κάθετη στην κεραία και διέρχεται από την μέση της. Παρατηρήστε ότι κατά μήκος της κεραίας δεν εκπέμπεται ισχύς. Γενικά θα μπορούσαμε να πούμε ότι η ισχύς που εκπέμπεται μεταβάλλεται με την γωνία από την κάθετο στην κεραία και με την απόσταση από την κεραία ως cos2θ/r2.
3. Κλασική Οπτική
3.1. Εισαγωγή
Στα επόμενα δύο κεφάλαια θα εξετάσουμε τα φαινόμενα και τις ιδιότητες των ηλεκτρομαγνητικών κυμάτων. Στο εξής ο όρος “φως” θα χρησιμοποιείται χωρίς διάκριση για όλη την ηλεκτρομαγνητική ακτινοβολία και όχι μόνο για το ορατό μέρος του φάσματος. Έτσι και αλλιώς τα φαινόμενα είναι κοινά και η μόνη διαφορά μεταξύ των ακτινοβολιών είναι το μήκος κύματος.
Ορισμένες από τις ιδιότητες όπως διάθλαση και ανάκλαση εξηγούνται απλά χωρίς ιδιαίτερη αναφορά στην κυματική φύση του φωτός. Οι ιδιότητες αυτές αποτελούν αντικείμενο μελέτης της λεγόμενης κλασικής ή γεωμετρικής οπτικής. Άλλες πάλι για να εξηγηθούν χρειάζεται να χρησιμοποιήσουμε το γεγονός ότι το φως είναι κύμα και αποτελούν αντικείμενο μελέτης της κυματικής οπτικής. Με τα φαινόμενα της κυματικής οπτικής θα ασχοληθούμε στο επόμενο κεφάλαιο.
3.2. Βασικές αρχές της κλασικής οπτικής
Μία βασική αρχή της κλασικής οπτικής είναι η προσέγγιση της ευθύγραμμης διάδοσης του φωτός. Δεχόμαστε δηλαδή ότι όταν το φως διαδίδεται σε ένα ομογενές και ισότροπο μέσο ακολουθεί μία ευθεία γραμμή η οποία ονομάζεται οπτική ή φωτεινή ακτίνα. Η οπτική ακτίνα είναι πάντα κάθετη στο μέτωπο του κύματος της ακτινοβολίας. Ως μέτωπο κύματος θεωρούμε την επιφάνεια στην οποία η εκπεμπόμενη ακτινοβολία έχει την ίδια φάση. Το φως από μία σημειακή πηγή έχει σφαιρικά μέτωπα κύματος. Αντίθετα μπορούμε να θεωρήσουμε ότι το φως που προέρχεται από ένα φακό που βρίσκεται σε μεγάλη απόσταση από τον παρατηρητή έχει στην περιοχή του παρατηρητή (τοπικά δηλαδή) επίπεδα μέτωπα κύματος και άρα οι οπτικές ακτίνες του είναι παράλληλες ευθείες.
Ο Huygens, το 1678, διατύπωσε την γνωστή αρχή του υποθέτοντας ότι το φως είναι κύμα. Ας σημειωθεί ότι δεν γνώριζε τίποτα από τις αρχές του Maxwell. Πως θα μπορούσε άλλωστε, αφού έζησε μόλις 200 χρόνια νωρίτερα! Σύμφωνα με την αρχή αυτή “κάθε σημείο του μετώπου ενός κύματος είναι πηγή δευτερογενών σφαιρικών κυμάτων. Το νέο μέτωπο κύματος ορίζεται ως η εφαπτόμενη επιφάνεια των μετώπων των δευτερογενών κυμάτων”. Στο Σχήμα 3.1 δίνεται με γραφικό τρόπο η αρχή του Huygens για την περίπτωση ενός σφαιρικού και ενός επιπέδου κύματος.
Τέλος ο Fermat λίγο νωρίτερα από τον Huygens διατύπωσε την αρχή με την οποία μπορούμε να προσδιορίσουμε την διαδρομή που θα ακολουθήσει το φως. Σύμφωνα με την αρχή του “το φως για να πάει από ένα σημείο Α σε ένα σημείο Β ακολουθεί την διαδρομή εκείνη για την οποία χρειάζεται ο μικρότερος χρόνος”. Προφανές αποτέλεσμα της αρχής αυτής είναι η ευθύγραμμη διάδοση του φωτός σε ένα ομογενές μέσο, γιατί η ευθεία είναι η συντομότερη διαδρομή. Προσοχή αυτό δεν ισχύει σε μη ομογενή μέσα, όπως θα δούμε στην συνέχεια.
3.3. Ανάκλαση
του φωτός
|
Σχήμα 3.1 Εφαρμογή της αρχής του Huygens και δημιουργία νέων μετώπων κύματος σε επίπεδα (αριστερά) και σφαιρικά (δεξιά) κύματα. |
Όταν μία φωτεινή ακτίνα που διαδίδεται σε ένα μέσο Α πέσει πάνω στην
διαχωριστική επιφάνεια ανάμεσα στο μέσο Α και σε ένα δεύτερο μέσο Β τότε ένα
μέρος της αρχικής ακτίνας ανακλάται πίσω και συνεχίζει την διάδοσή του στο μέσο
Α.
Έστω τώρα ότι πάνω στην διαχωριστική επιφάνεια πέφτει μία δέσμη παραλλήλων ακτίνων. Αν η διαχωριστική επιφάνεια είναι λεία τότε η ανακλώμενες ακτίνες συνεχίζουν να είναι παράλληλες μεταξύ τους. Η ανάκλαση αυτή λέγεται κατοπτρική ανάκλαση και υλικά μέσα με τέτοιες λείες επιφάνειες ονομάζονται κάτοπτρα. Αν όμως η επιφάνεια έχει ανωμαλίες, είναι τραχιά όπως συνήθως λέμε, τότε κάθε ακτίνα θα ανακλάται σε διαφορετική διεύθυνση και θα διασκορπίζονται στον γύρω χώρο. Η περίπτωση αυτή ονομάζεται διάχυση. Η διάχυση είναι πολύ σημαντικό φαινόμενο. Χάρη σ’ αυτήν το φως μπαίνει μέσα στο δωμάτιο ακόμη και όταν ο Ήλιος δεν πέφτει στα παράθυρα. Επίσης χάρη σ’ αυτήν είναι δυνατόν να βλέπουμε τα διάφορα αντικείμενα! Σκεφτείτε λίγο έναν τέλειο καθρέφτη. Τι βλέπετε όταν κοιτάτε σ΄ αυτόν ; Τον καθρέφτη; Όχι! Βλέπετε τα διάφορα αντικείμενα που διαχέουν το φως και κατοπτρίζονται στον καθρέφτη! Γενικά θα μπορούσαμε να πούμε ότι μία επιφάνεια μπορεί να θεωρηθεί καλό κάτοπτρο όταν οι ανωμαλίες της είναι μικρές σε σχέση με το μήκος κύματος της προσπίπτουσας ακτινοβολίας. Έτσι για παράδειγμα η επιφάνεια μίας δορυφορικής κεραίας είναι αρκετά ανώμαλη για την ορατή ακτινοβολία και διαχέει το ορατό φως. Από την άλλη όμως η ανωμαλίες της είναι πολύ μικρές σε σχέση με το μήκος κύματος των ραδιοκυμάτων που είναι της τάξης των μερικών εκατοστών έως μερικών μέτρων. Γι’ αυτό στα ραδιοκύματα λειτουργεί σαν κάτοπτρο.
Στο εξής όταν θα αναφερόμαστε σε ανάκλαση θα εννοούμε την κατοπτρική ανάκλαση. Όταν λοιπόν μία φωτεινή ακτίνα ανακλάται από μία επιφάνεια τότε ισχύει ο νόμος της ανάκλασης που μας λέει ότι η γωνία ανακλάσεων, που είναι η γωνία της ανακλώμενης ακτίνας με την κάθετο στην επιφάνεια στο σημείο γίνεται η ανάκλαση είναι ίση με την γωνία προσπτώσεως, που είναι η γωνία της προσπίπτουσας ακτίνας με την κάθετο στην επιφάνεια. Σχηματικά ο νόμος της ανάκλασης παρουσιάζεται στο Σχήμα 3.2
3.4. Διάθλαση του φωτός.
Είδαμε προηγουμένως ότι όταν μια ακτίνα πέσει πάνω σε μία διαχωριστική επιφάνεια του μέσου που διαδίδεται και ενός άλλου μέσου, τότε ένα μέρος της ανακλάται. Το άλλο μέρος την όμως περνάει μέσα στο δεύτερο μέσο αλλάζοντας όμως πορεία διάδοσης. Λέμε τότε ότι η ακτίνα διαθλάται. Η προσπίπτουσα, η ανακλώμενη και η διαθλώμενη ακτίνα είναι πάντα στο ίδιο επίπεδο.
Έστω λοιπόν έχουμε δύο μέσα (1) και (2) και η φωτεινή ακτίνα περνά από το μέσο (1) στο μέσο (2) όπως στο Σχήμα 3.3 Στο μέσο (1) το φως διαδίδεται με ταχύτητα υ1 ενώ στο μέσο (2) με ταχύτητα υ2. Αν θ1 η γωνία πρόσπτωσης και θ2 η γωνία διάθλασης, ο νόμος της διάθλασης μας λέει ότι
|
(3.1) |
Ο νόμος αυτός ονομάζεται νόμος του Snell. Από την σχέση (3.1) είναι προφανές ότι όταν η ακτίνα περάσει από ένα οπτικώς αραιότερο μέσο σε ένα οπτικώς πυκνότερο, δηλαδή όταν υ1>υ2 τότε η γωνία διάθλασης θ2 είναι μικρότερη από την γωνία πρόσπτωσης θ1. Το αντίθετο συμβαίνει όταν η οπτική ακτίνα ακολουθεί την αντίθετη διαδρομή.
Όταν το φως διαδίδεται στο κενό η ταχύτητα του είναι όπως είπαμε ίση με c που (χοντρικά) είναι ίσο με 300.000 km/s = 3 108 m/s. Όταν όμως διαδίδεται σε κάποιο υλικό μέσο η ταχύτητα του είναι μικρότερη. Στο γυαλί για παράδειγμα είναι περίπου στα 200.000 km/s, εξαρτάται βέβαια από το είδος και την ποιότητα του γυαλιού. Ορίζουμε ως δείκτη διάθλασης ενός μέσου τον λόγο της ταχύτητας του φωτός στο κενό προς την ταχύτητα του φωτός στο μέσο. Δηλαδή
|
|
(3.2) |
Φυσικά ο δείκτης διάθλασης για οποιοδήποτε άλλο, εκτός του κενού, μέσο είναι πάντα μεγαλύτερος της μονάδος. Το ότι το n ³ 1 είναι αποτέλεσμα και μιας άλλης πολύ σημαντικής θεωρίας, της Θεωρίας της Ειδικής Σχετικότητας του Einstein, η οποία μας λέει ότι η ταχύτητα c είναι γενικά η μεγαλύτερη ταχύτητα που μπορεί να επιτευχθεί στο σύμπαν.
Επιστρέφοντας στο φαινόμενο της διάθλασης, μπορούμε τώρα να χρησιμοποιώντας τον ορισμό του δείκτη διάθλασης να ξαναγράψουμε τον νόμο του Snell ως
|
|
(3.3) |
Η συχνότητα του φωτός όταν αυτό διέρχεται από το ένα μέσο σε ένα άλλο δεν αλλάζει. Αυτό προκύπτει εύκολα από το θεώρημα διατήρησης της ενέργειας των φωτονίων όπως θα δούμε σε επόμενο κεφάλαιο.
Η ταχύτητα του φωτός σε ένα μέσο σχετίζονται, ως γνωστόν, με την συχνότητα και το μήκος κύματος με την σχέση
|
|
(3.4) |
Άρα λοιπόν για τα μέσα (1) και (2) έχουμε
|
|
(3.5) |
και από τον ορισμό του δείκτη διάθλασης έχουμε
|
|
(3.6) |
Βλέπουμε λοιπόν ότι όταν το φως διαδίδεται από ένα οπτικά αραιότερο μέσο σε ένα οπτικά πυκνότερο, δηλαδή όταν n1<n2 ή ισοδύναμα υ1>υ2, τότε το μήκος κύματος του φωτός μειώνεται. Στο Σχήμα 3.4 παρουσιάζεται η μεταβολή του μήκους κύματος της ακτινοβολίας όταν αυτή εισέρχεται από οπτικά αραιότερο σε οπτικά πυκνότερο μέσο.
Στον παρακάτω πίνακα αναφέρονται ενδεικτικά οι δείκτες διάθλασης ορισμένων συνηθισμένων υλικών.
|
Υλικό |
Δείκτης διάθλασης |
|
Διαμάντι |
2.419 |
|
Στεφανούαλος |
1.52 |
|
Πάγος |
1.309 |
|
Νερό |
1.333 |
|
Αέρας |
1.000293 |
Όπως βλέπουμε ο δείκτης διάθλασης του αέρα είναι σχεδόν ίσος με την μονάδα. Για τον λόγο αυτό σε πολλές εφαρμογές παίρνεται ίσος με την μονάδα και η ταχύτητα του φωτός στον αέρα ίση με την ταχύτητα του φωτός στο κενό.
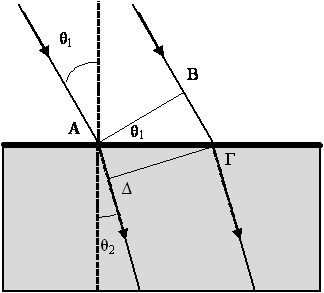
Ας αποδείξουμε τώρα τον νόμο του Snell χρησιμοποιώντας τις αρχές του Huygens και Fermat. Ας ξεκινήσουμε με την αρχή του Huygens και ας πάρουμε δύο παράλληλες
οπτικές ακτίνες που πέφτουν στην διαχωριστική επιφάνεια των δύο μέσων (Σχήμα 3.5)
Η γραμμή ΑΒ παριστάνει ένα μέτωπο κύματος στο μέσο (1) ενώ η γραμμή ΔΓ ένα μέτωπο κύματος στο μέσο (2). Από το σχήμα είναι προφανές ότι η γωνία ΒΑΓ είναι ίση με την γωνία πρόσπτωσης θ1, ως γωνίες που έχουν τις πλευρές τους κάθετες μεταξύ του. Η γωνία ΑΓΔ είναι ίση με την γωνία διάθλασης θ2 για τον ίδιο λόγο.
Επειδή τα ΑΒ και ΔΓ είναι μέτωπα κύματος, ο χρόνος που χρειάζεται το φως για να καλύψει την απόσταση από ένα σημείο του παλαιού μετώπου κύματος στο αντίστοιχο σημείο του νέου μετώπου είναι ο ίδιος για όλα τα σημεία του μετώπου. Έτσι αν Δt o χρόνος που χρειάζεται το φως για να καλύψει την απόσταση ΑΔ, τότε και ο χρόνος για να καλύψει την απόσταση ΒΓ είναι επίσης Δt. Τα διαστήματα ΑΔ και ΒΓ όμως βρίσκονται σε διαφορετικά μέσα το καθένα και άρα καλύπτονται με διαφορετικές ταχύτητες. Έτσι λοιπόν έχουμε
|
|
(3.7) |
|
|
(3.8) |
Το ημίτονο της γωνίας ΒΑΓ είναι, ως γνωστό, ίσο με το μήκος της ΒΓ προς το μήκος της ΑΓ. Αντίστοιχα το ημίτονο της γωνίας ΑΓΔ είναι ίσο με ΑΔ προς ΑΓ. Άρα λοιπόν
|
|
(3.9) |
|
|
(3.10) |
Διαιρούμε τις δύο εξισώσεις κατά μέλη και λαμβάνοντας υπόψη τον ορισμό του δείκτη διάθλασης καταλήγουμε στον νόμο του Snell.
|
|
(3.11) |
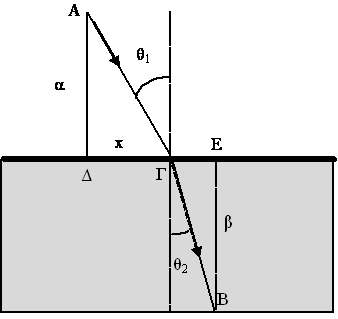
Ας δούμε τώρα πως μπορούμε να καταλήξουμε στο ίδιο αποτέλεσμα ακολουθώντας την αρχή του Fermat. Υπενθυμίζουμε ότι η αρχή αυτή λέει ότι το φως για να πάει από το σημείο Α στο σημείο Β θα ακολουθήσει την διαδρομή του μικρότερου χρόνου (που δεν είναι πάντα η διαδρομή της μικρότερης απόστασης). Ας δούμε το Σχήμα 3.6. Έστω ότι το φως θα πάει από το σημείο Α στο Β ακολουθώντας την διαδρομή ΑΓΒ. Ενδιαφερόμαστε να βρούμε τη θέση x του σημείου Γ.
Ο χρόνος που χρειάζεται το φως για να πάει από το σημείο Α στο Β είναι το άθροισμα του χρόνου που χρειάζεται για να καλύψει τις αποστάσεις ΑΓ και ΓΒ. Αν υ1 η ταχύτητα στο μέσο (1) τότε ο χρόνος που χρειάζεται για να καλύψει την απόσταση ΑΓ είναι ίσος με ΑΓ/υ1. Αντίστοιχα ο απαραίτητος χρόνος για να καλυφθεί η απόσταση ΓΒ είναι ΓΒ/υ2. Ο συνολικός χρόνος λοιπόν θα είναι
Από τα τρίγωνα ΑΔΓ και ΓΕΒ έχουμε
|
|
(3.13) |
και
|
|
(3.14) |
οπότε η σχέση (3.12) γράφετε
|
|
(3.15) |
Η τιμή του x που αντιστοιχεί στον ελάχιστο χρόνο είναι η τιμή στην οποία η παράγωγος του χρόνου ως προς x μηδενίζεται. Παραγωγίζουμε λοιπόν την προηγούμενη σχέση ως προς x και βρίσκουμε
Παρατηρώντας λοιπόν ξανά το Σχήμα 3.6 βλέπουμε ότι
|
|
(3.17) |
και
|
|
(3.18) |
οπότε η σχέση (3.16) γράφεται
|
|
(3.19) |
Καταλήγουμε δηλαδή στον νόμο της διάθλασης του Snell.
Με τον ίδιο τρόπο θα μπορούσαμε να αποδείξουμε τον νόμο της ανάκλασης χρησιμοποιώντας την αρχή του Fermat ή του Huygens. Οι αποδείξεις με τις δύο αυτές αρχές είναι αρκετά απλές και αφήνονται σαν άσκηση στους σπουδαστές.
3.5. Ολική εσωτερική ανάκλαση
Ας πάρουμε τώρα την περίπτωση που φωτεινές ακτίνες διαδίδονται από ένα οπτικά πυκνότερο μέσο σε ένα οπτικά αραιότερο. Πάλι, όπως είναι φυσικό, ισχύει ο νόμος της διάθλασης του Snell.
|
Σχήμα 3.7 Διάθλαση και ανάκλαση του φωτός όταν διέρχεται από οπτικώς πυκνότερο σε οπτικώς αραιότερο μέσο. |
Μόνο που αυτή την φορά n1>n2. Από την σχέση (3.20) βρίσκουμε ότι η γωνία θ1 είναι ίση με
![]()
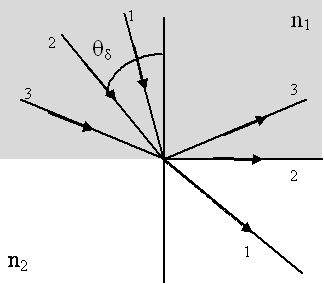
αλλά n2<n1 Þ n2 / n1<1. Αλλά και το sin θ2 είναι από τον ορισμό του ημιτόνου, μικρότερο ή ίσο με την μονάδα. Άρα καταλήγουμε ότι το sin θ1<1 για κάθε τιμή του θ2. Με άλλα λόγια για να έχουμε διάθλαση η γωνία πρόσπτωσης θ1 μπορεί να πάρει τιμές από 0° μέχρι μία οριακή γωνία θδ για την οποία η διαθλώμενη ακτίνα έχει γωνία διάθλασης την μέγιστη γωνία δηλαδή 90°. Η γωνία θδ είναι ίση με
|
|
(3.21) |
Για γωνίες πρόσπτωσης μεγαλύτερες της θδ προφανώς δεν
μπορεί να υπάρξει διάθλαση και η οπτική ακτίνα ανακλάται ολικά. Για τον λόγο
αυτό η γωνία θδ ονομάζεται γωνία ολικής ανάκλασης.
Προσοχή όμως, το φαινόμενο της ολικής ανάκλασης μπορεί να συμβεί μόνο αν n2<n1, δηλαδή όταν το φως προσπαθεί να διέλθει από οπτικώς
πυκνότερο μέσο σε οπτικώς αραιότερο. Στο Σχήμα 3.8
βλέπουμε παρουσιάζονται οι οπτικές διαδρομές τριών ακτίνων. Η ακτίνα 1
διαθλάται κανονικά ενώ η ακτίνα 2 προσπίπτει με γωνία ίση με την γωνία ολικής
ανάκλασης. Η διαθλώμενη στην περίπτωση αυτή κατευθύνεται παράλληλα προς την
διαχωριστική επιφάνεια. Τέλος η ακτίνα 3 προσπίπτει με γωνία μεγαλύτερη της
γωνίας ολικής ανάκλασης και ανακλάται πλήρως συνεχίζοντας την διάδοση της στο
μέσο 1.
Ίσως να μην το έχετε σκεφτεί αλλά στο φαινόμενο της ολικής ανάκλασης οφείλεται η λάμψη των διαμαντιών! Το διαμάντι έχει πολύ μεγάλο δείκτη διάθλασης n = 2.42. Άρα η γωνία διάθλασης της επιφάνειας διαμάντι-αέρας έχει γωνία ολικής ανάκλασης που είναι θδ=arcsin(1/2.42)=24°. Κόβοντας λοιπόν το διαμάντι με πολλές έδρες αυτά λάμπουν γιατί το φως εισέρχεται στο διαμάντι και υφίσταται πολλές διαδοχικές ολικές ανακλάσεις στις διάφορες έδρες του. Έτσι το μεγαλύτερο μέρος του φωτός εξέρχεται από την εμπρόσθια πλευρά κάνοντας το να λάμπει.
3.6. Οπτικές ίνες
Μια πολύ σημαντική εφαρμογή του φαινομένου της ολικής ανάκλασης είναι η χρησιμοποίηση λεπτών σωλήνων γυαλιού, των λεγόμενων οπτικών ινών, για την οδήγηση του φωτός σε οποιαδήποτε σημείο επιθυμούμε ακόμη και γύρω από γωνίες.
Μία οπτική ίνα αποτελείται από ένα πολύ λεπτό σωλήνα γυαλιού ο οποίος είναι τόσο πιο εύκαμπτος όσο πιο λεπτός είναι. Για τον λόγο αυτό προτιμάται η χρήση μιας δέσμης από λεπτές οπτικές ίνες παρά η χρήση ενός χονδρότερου αγωγού. Το φως εισέρχεται στην οπτική ίνα από την μία άκρη της και καθώς διαδίδεται μέσα σ΄ αυτήν υφίσταται διαδοχικές ολικές ανακλάσεις στα τοιχώματα της. Έτσι εξέρχεται από το άλλο άκρο της χωρίς να υποστεί σημαντική μείωση της έντασης της (Σχήμα 3.9).
Οι οπτικές ίνες, οι οποίες επίσης ονομάζονται και φωταγωγοί, έχουν αρκετές σημαντικές εφαρμογές. Στην ιατρική για παράδειγμα χρησιμοποιούνται για ενδοσκόπηση. Οι γιατροί για παράδειγμα για να δουν το εσωτερικό του στομάχου χρησιμοποιούν μια δέσμη οπτικών ινών. Μια άλλη δέσμη χρησιμοποιείται σαν κατευθυνόμενος φακός για να φωτίσει το εσωτερικό του στομάχου.
Τελευταία, οπτικές ίνες χρησιμοποιούνται για μετάδοση πληροφοριών αντικαθιστώντας τα παλαιά μεταλλικά καλώδια. Η ταχύτητα μετάδοσης των πληροφοριών στις οπτικές ίνες είναι τεράστια, σε σύγκριση με τα κοινά χάλκινα καλώδια, με αποτέλεσμα τεράστιος όγκος πληροφοριών να μπορεί να μεταδοθεί με μία μόνο οπτική ίνα.
4. Κυματική Οπτική
4.1. Εισαγωγή
Στο προηγούμενο κεφάλαιο εξετάσαμε φαινόμενα που μπορούν να εξηγηθούν με την απλή γεωμετρική οπτική, χωρίς δηλαδή να γίνεται συγκεκριμένη αναφορά στην κυματική φύση του φωτός.
Στο παρόν κεφάλαιο θα μελετήσουμε φαινόμενα που μπορούν να εξηγηθούν μόνο αν δεχθούμε πως το φως είναι κύμα. Το μέρος αυτό της οπτικής που ασχολείται με την κυματική φύση των ηλεκτρομαγνητικών ακτινοβολιών ονομάζεται Κυματική Οπτική. Φαινόμενα όπως η συμβολή, η περίθλαση και η πόλωση εξηγούνται μόνο με την κυματική οπτική.
4.2. Πόλωση του φωτός
Στο Κεφάλαιο 2 είδαμε ότι η ηλεκτρομαγνητική ακτινοβολία είναι εγκάρσια κύματα που διαδίδονται στον χώρο. Ο χαρακτηρισμός εγκάρσια σημαίνει ότι το διάνυσμα του ηλεκτρικού και του μαγνητικού πεδίου ταλαντώνονται κάθετα προς την διεύθυνση διάδοσης του κύματος.
Είδαμε ότι στα κύματα που δημιουργούνται από μία διπολική κεραία και διαδίδονται κατά μήκος μιας ευθείας κάθετης στο μέσον του άξονα του διπόλου το ηλεκτρικό πεδίο ταλαντώνεται κατά την διεύθυνση του άξονα του διπόλου και το μαγνητικό πεδίο κατά την διεύθυνση την κάθετη προς το επίπεδο που ορίζουν η διεύθυνση διάδοσης και η διεύθυνση ταλάντωσης του ηλεκτρικού πεδίου, όπως είχαμε δει και στο Σχήμα 2.1. Το φως στο οποίο το ηλεκτρικό πεδίο και κατά συνέπεια και το μαγνητικό πεδίο, ταλαντώνεται κατά μία συγκεκριμένη διεύθυνση ονομάζεται πολωμένο.
Ας πάρουμε την περίπτωση η φωτεινή πηγή μας να είναι μια συνηθισμένη πηγή φωτός π.χ. μία κοινή λάμπα πυρακτώσεων. Στην περίπτωση αυτή το φως δεν προέρχεται από ένα μόνο άτομο της πηγής. Κάθε άτομο ακτινοβολεί το δικό του φως που έχει το δικό του επίπεδο πόλωσης. Το φως όμως που παίρνουμε από όλη την πηγή σχηματίζεται από την υπέρθεση των κυμάτων που εκπέμπουν όλα τα άτομα. Έτσι το φως που προκύπτει από αυτή την υπέρθεση δεν έχει κανένα συγκεκριμένο επίπεδο πόλωσης. Το φως αυτό λέγεται μη πολωμένο ή απλά φυσικό φως.
Έστω λοιπόν ότι σε κάποια χρονική στιγμή, μία φωτεινή δέσμη που διαδίδεται κατά τον άξονα z, το διάνυσμα του ηλεκτρικού του πεδίου E σχηματίζει γωνία θ με τον άξονα x. Όπως φαίνεται και στο Σχήμα 4.1, μπορούμε να αναλύσουμε το διάνυσμα Ε σε δύο συνιστώσες Εx και Ey.
Αν η γωνία θ παραμένει σταθερή με τον
χρόνο, δηλαδή τα Εx και Ey ταλαντώνονται με την ίδια φάση, τότε
το Ε ταλαντώνεται κατά την ίδια πάντα διεύθυνση και το φως όπως είπαμε
πριν ονομάζεται γραμμικά πολωμένο ή επίπεδα πολωμένο.
Αν αντίθετα τα Εx και Ey έχουν ίσες μέγιστες τιμές αλλά διαφορά φάσης 90° τότε το διάνυσμα Ε διαγράφει περιφέρεια κύκλου και το φως λέμε ότι είναι κυκλικά πολωμένο. Ενώ αν δεν έχουν ίσες μέγιστες τιμές, το Ε διαγράφει περιφέρεια έλλειψης και το φως είναι ελλειπτικά πολωμένο. Τέλος αν η φάση είναι τυχαία και αλλάζει με τον χρόνο τότε το φως δεν είναι πολωμένο. Βλέπουμε λοιπόν ότι υπάρχουν διάφορα είδη πόλωσης. Συνήθως όμως όταν αναφέρουμε τον όρο πολωμένο φως αναφερόμαστε στο γραμμικά πολωμένο φως.
Για να πάρουμε πολωμένο φως από μία πηγή φυσικού (μη πολωμένου) φωτός θα πρέπει να μπορέσουμε να αφαιρέσουμε όλα τα κύματα εκτός από αυτά τα οποία ταλαντώνονται σε ένα συγκεκριμένο επίπεδο. Θα περιγράψουμε παρακάτω μερικές από τις διεργασίες που έχουν σαν αποτέλεσμα την παραγωγή πολωμένου φωτός.
4.2.1. Πόλωση με επιλεκτική απορρόφηση.
Ο πιο συνηθισμένος τρόπος παραγωγής πολωμένου φωτός είναι με την χρήση ειδικών φίλτρων, διαφανή υλικά, τα οποία αφήνουν να διέλθουν από μέσα τους ηλεκτρομαγνητικά κύματα που το ηλεκτρικό τους πεδίο ταλαντώνεται κατά μία ορισμένη διεύθυνση που ονομάζεται διεύθυνση διάδοσης και απορροφούν πλήρως τα κύματα που ταλαντώνονται κάθετα προς την διεύθυνση αυτή. Για κάθε άλλο κύμα που ταλαντώνεται πλάγια προς την διεύθυνση διάδοσης επιτρέπουν να διέλθει η συνιστώσα του πεδίου η παράλληλη προς την διεύθυνση διάδοσης, με αποτέλεσμα το κύμα να εξέλθει πολωμένο αλλά με μικρότερη ένταση.
Τα υλικά αυτά λέγονται διχροϊκά. Ένα τέτοιο υλικό κατασκεύασε πρώτος ο Land το 1938 και το ονόμασε Polaroid. Αποτελείται από μακριά μόρια
πολυμερών υδατανθράκων π.χ. πολυβινυλική αλκοόλη, τα οποία κατά την διάρκεια
παραγωγής του υλικού τεντώνονται έτσι ώστε οι αλυσίδες τους προσανατολίζονται
όλες κατά την ίδια διεύθυνση. Τα ηλεκτρόνια αγωγιμότητας των μορίων μπορούν να
κινούνται μόνο κατά την διεύθυνση των αλυσίδων. Αν πάνω τους πέσει
ηλεκτρομαγνητική ακτινοβολία με επίπεδο ταλάντωσης παράλληλο με την διεύθυνση
των αλυσίδων, τα ηλεκτρόνια αγωγιμότητας την απορροφούν και ταλαντώνονται κατά
την διεύθυνση των αλυσίδων. Στην αντίθετη περίπτωση που η ακτινοβολία έχει
επίπεδο ταλάντωσης κάθετο προς την διεύθυνση των αλυσίδων τα ηλεκτρόνια δεν
μπορούν να την απορροφήσουν γιατί δεν μπορούν να ταλαντωθούν κατά την διεύθυνση
αυτή. Το ίδιο ακριβώς φαινόμενο συμβαίνει και στην περίπτωση του πλέγματος
πόλωσης που χρησιμοποιείται στο εργαστήριο του μαθήματος Φυσική ΙΙ. Ένα ιδανικό
υλικό πόλωσης απορροφά όλη την ακτινοβολία της οποίας το διάνυσμα E είναι κάθετο στον άξονα διάδοσης ενώ
επιτρέπει να περάσει όλη η ακτινοβολία της οποίας το Ε είναι
παράλληλο.
Ας πάρουμε τώρα την διάταξη που παρουσιάζεται στο Σχήμα 4.2. Τα δύο πολωτικά υλικά έχουν άξονες διάδοσης που σχηματίζουν μεταξύ τους γωνία θ. Φυσικό μη πολωμένο φως πέφτει πάνω στο πρώτο υλικό που ονομάζεται πολωτής. Το φως που εξέρχεται του πολωτή είναι γραμμικά πολωμένο με διεύθυνση ταλάντωσης την διεύθυνση του άξονα διάδοσης του πολωτή. Έστω ότι η ένταση του ηλεκτρικού πεδίου μετά τον πολωτή είναι ΕΠ. Το φως, στην συνέχεια διέρχεται μέσα από το δεύτερο πολωτικό υλικό που ονομάζεται αναλυτής. Αν αναλύσουμε το διάνυσμα ΕΠ σε δύο συνιστώσες, μία παράλληλη προς τον άξονα διάδοσης του αναλυτή και μία κάθετη προς τον άξονα διάδοσης, τότε όπως έχουμε προαναφέρει ο αναλυτής θα αφήσει να περάσει μόνο η παράλληλη προς τον άξονά του συνιστώσα του πεδίου. Δηλαδή μετά τον αναλυτή η ένταση του πεδίου θα είναι
|
|
(4.1) |
Επομένως η ένταση του διαδιδόμενου φωτός, η οποία είναι ανάλογη του τετραγώνου της έντασης του πεδίου, θα είναι
|
|
(4.2) |
Η σχέση αυτή αποτελεί την μαθηματική έκφραση του νόμου του Malus. Βλέπουμε λοιπόν ότι μεταβάλλοντας την γωνία μεταξύ δύο πολωτών μπορούμε να επιτύχουμε η διερχόμενη ένταση του φωτός να παίρνει από μία μέγιστη τιμή έως και την τιμή μηδέν.
4.2.2. Πόλωση από ανάκλαση
Ένας άλλος τρόπος παραγωγής πολωμένου φωτός είναι η πόλωση με ανάκλαση. Έχει παρατηρηθεί ότι όταν μία μη πολωμένη δέσμη φωτός ανακλαστεί πάνω σε μία οριζόντια επιφάνεια τότε η οριζόντια συνιστώσα του ηλεκτρικού πεδίου ανακλάται περισσότερο από την κάθετη συνιστώσα. Γενικά το ανακλώμενο φως είναι μερικώς πολωμένο. Μερικά πολωμένο είναι και το διαθλώμενο.
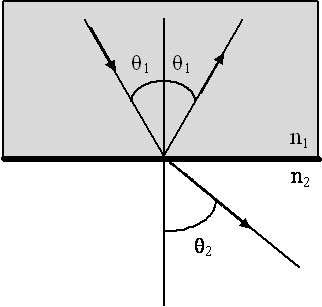
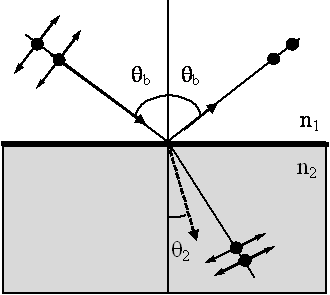
Υπάρχει όμως μία γωνία πρόσπτωσης θb στην οποία το ανακλώμενο φως είναι ολικά πολωμένο με επίπεδο πόλωσης παράλληλο προς την διαχωριστική επιφάνεια. Αυτό συμβαίνει όταν η ανακλώμενη και η διαθλώμενη ακτίνα σχηματίζουν μεταξύ τους γωνία 90°. Ας σημειωθεί ότι η διαθλώμενη εξακολουθεί να είναι μερικώς πολωμένη. Το φαινόμενο παρουσιάζεται στο Σχήμα 4.3. Με τα βέλη αναπαριστούμε την συνιστώσα του πεδίου που είναι κάθετη στην επιφάνεια ανάκλασης (και παράλληλα με την σελίδα του βιβλίου) και με τις τελείες την συνιστώσα που είναι παράλληλη με την επιφάνεια ανάκλασης (και που είναι κάθετη στην επιφάνεια του βιβλίου).
Αν εφαρμόσουμε τον νόμο του Snell στην περίπτωση αυτή έχουμε
Αλλά από το σχήμα βλέπουμε ότι θb+θ2=90°, άρα
|
|
(4.4) |
και η σχέση (4.3) γράφεται
|
|
(4.5) |
Η σχέση αυτή είναι η μαθηματική έκφραση του νόμου του Brewster και η γωνία θb ονομάζεται γωνία Brewster.
Η πόλωση από ανάκλαση είναι ένα συνηθισμένο φαινόμενο. Το φως του ήλιου πολώνεται από την ανάκλαση του στις επιφάνειες του νερού, του πάγου κ.λ.π. Αν η ανακλώσα επιφάνεια είναι οριζόντια π.χ. η επιφάνεια της θάλασσας, τότε το ανακλώμενο φως έχει μεγάλη οριζόντια συνιστώσα. Με άλλα λόγια το φως στις παραλίες είναι μερικώς πολωμένο με μεγάλη οριζόντια συνιστώσα. Για τον λόγο αυτό και τα γυαλιά ηλίου τύπου Polaroid έχουν τον άξονα διάδοσης κάθετο, έτσι ώστε να απορροφούν την μεγάλη οριζόντια συνιστώσα του φωτός.
Πόλωση του φωτός μπορούμε να έχουμε και από άλλες διεργασίες. Έτσι έχουμε πόλωση από σκέδαση, πόλωση από διπλοδιαθλαστικά υλικά κ.λ.π.
4.3. Συμβολή του φωτός.
Όταν σε ένα σημείο του χώρου διαδίδονται ταυτόχρονα δύο ή περισσότερα ηλεκτρομαγνητικά κύματα τότε το φως στο σημείο αυτό είναι το αποτέλεσμα της επιπρόσθεσης όλων των κυμάτων. Το φαινόμενο αυτό ονομάζεται συμβολή και τα κύματα λέμε ότι συμβάλουν στο συγκεκριμένο σημείο.
Το φαινόμενο της συμβολής είναι κοινό για όλα τα κύματα, όχι μόνο τα ηλεκτρομαγνητικά. Δεν είναι όμως εύκολο να παρατηρήσουμε στην καθημερινή μας ζωή την συμβολή του φωτός γιατί το μήκος κύματος του ορατού φωτός είναι πολύ μικρό.
Για να μπορέσουμε να παρατηρήσουμε στάσιμη συμβολή, δηλαδή συμβολή στην οποία τα αποτελέσματα είναι σταθερά και δεν μεταβάλλονται με τον χρόνο πρέπει να ισχύουν ορισμένες προϋποθέσεις. Συγκεκριμένα
1. Οι δύο πηγές φωτός τα κύματα των οποίων συμβάλουν να είναι μονοχρωματικές, δηλαδή να εκπέμπουν σε ένα μόνο μήκος κύματος το οποίο να είναι το ίδιο και στις δύο πηγές.
2. Να είναι σύμφωνες δηλαδή να έχουν πάντα την αυτή σταθερή διαφορά φάσης μεταξύ τους.
Η απαίτηση του να είναι σύμφωνες δύο πηγές φωτός είναι πολύ δύσκολο να επιτευχθεί. Αυτό γιατί οποιαδήποτε κοινή πηγή φωτός μεταβάλει το εκπεμπόμενο φως σε πολύ μικρά χρονικά διαστήματα π.χ. μία λάμπα πυρακτώσεως μεταβάλει το φως σε διάστημα της τάξης των μερικών δισεκατομμυριοστών του δευτερολέπτου. Επομένως και τα αποτελέσματα της συμβολής αλλάζουν και αυτά ακολουθώντας αυτό τον πολύ γρήγορο ρυθμό. Αλλά ως γνωστό το μάτι μας δεν μπορεί να αναγνωρίσει αλλαγές που γίνονται σε διαστήματα μικρότερα των μερικών εκατοστών του δευτερολέπτου. Έτσι δεν μπορούμε να αντιληφθούμε τα αποτελέσματα μιας τέτοιας συμβολής.
Μπορούμε να δημιουργήσουμε δύο σύμφωνες πηγές χρησιμοποιώντας το φως μίας μόνο μονοχρωματικής πηγής και ένα πέτασμα με δύο οπές. Το φως της πηγής πέφτει επάνω στο πέτασμα και διέρχεται μόνο από τις δύο οπές. Σύμφωνα με την αρχή του Huygens οι δύο οπές δρουν ως πηγές δευτερογενών κυμάτων. Το φως φυσικά των δύο πηγών είναι σύμφωνο μιας και προέρχεται από μία και την αυτή πηγή. Μάλιστα αν η απόσταση των δύο οπών από την πηγή είναι η ίδια τότε το φως που εκπέμπουν οι δύο οπές έχει την ίδια φάση. Σημειώστε ότι οι οπές ή σχισμές (όπως χρησιμοποίησε ο Young) πρέπει να έχουν διαστάσεις μικρότερες του μήκους κύματος.
Ας δούμε τώρα τι θα συμβεί όταν τα δύο κύματα από τις δύο οπές συμβάλουν σε ένα σημείο του χώρου Σ (Σχήμα 4.4). Το ηλεκτρικό πεδίο του κύματος που προέρχεται από την οπή (1) είναι την χρονική στιγμή t, στο σημείο Σ, ίσο με
|
|
(4.6) |
όπου x1 η απόσταση του Σ από την οπή (1). Αντίστοιχα το ηλεκτρικό πεδίο του κύματος της οπής (2) θα είναι
|
|
(4.7) |
Το συνιστάμενο κύμα στο σημείο Σ προέρχεται από την πρόσθεση των Ε1 και Ε2 και θα είναι
Από την τριγωνομετρία γνωρίζουμε ότι
Χρησιμοποιώντας την τριγωνομετρική ταυτότητα (4.9) η σχέση (4.8) γράφεται
|
|
(4.10) |
Δηλαδή το συνιστάμενο πεδίο στο σημείο Σ εκτελεί αρμονική ταλάντωση με την αυτή συχνότητα (f = ω/2π) αλλά το πλάτος της είναι ίσο με
όπου στη τελευταία σχέση αντικαταστήσαμε τον κυματάριθμο k με 2π/λ και την διαφορά διαδρομής x1-x2 την συμβολίσαμε με δ. Βλέπουμε λοιπόν ότι τα δύο κύματα συμβάλουν και το πλάτος του συνιστάμενου κύματος εξαρτάται από την διαφορά διαδρομής. Αν η διαφορά διαδρομής δ είναι ακέραιο πολλαπλάσιο του μήκους κύματος λ τότε τα κύματα συμβάλουν ενισχυτικά. Αντίθετα αν η διαφορά διαδρομές είναι ημιακέραιο μήκος κύματος, με άλλα λόγια περιττό πολλαπλάσιο του μισού μήκους κύματος δηλαδή δ = (2κ+1)λ/2, τα κύματα συμβάλουν καταστρεπτικά και το συνιστάμενο πεδίο είναι μηδέν.
Αν τοποθετήσουμε, σε μεγάλη απόσταση από τις δύο οπές, ένα πέτασμα τότε μπορούμε επάνω του να παρατηρήσουμε την εικόνα συμβολής των δύο πηγών. Μια τέτοια εικόνα φαίνεται στο Σχήμα 4.5. Όπως βλέπουμε αποτελείται από διαδοχικές φωτεινές και σκοτεινές ζώνες που ονομάζονται κροσσοί συμβολής (φωτεινοί και σκοτεινοί αντίστοιχα).
Επειδή η απόσταση L του πετάσματος είναι πολύ μεγάλη σε σχέση με την απόσταση d των δύο πηγών μπορούμε χωρίς να κάνουμε μεγάλο λάθος να δεχθούμε ότι η διαφορά διαδρομής είναι ίση με
Έτσι έχουμε ενισχυτική συμβολή, δηλαδή φωτεινό κροσσό όταν
όπου m ακέραιος αριθμός που ονομάζεται αριθμός τάξης του κροσσού.
Εφόσον δεχθήκαμε ότι L είναι πολύ μεγαλύτερο του d τότε
Έτσι από τις σχέσεις (4.13) και (4.14) μπορούμε να υπολογίσουμε την θέση των φωτεινών κροσσών
Παρόμοια υπολογίζουμε και τις θέσεις των σκοτεινών κροσσών.
Η ένταση του φωτός σε ένα σημείο σε μία εικόνα συμβολής όπως αυτή του Σχήματος 4.5, είναι όπως είπαμε ο μέσος όρος του τετραγώνου της έντασης του ηλεκτρικού πεδίου. Έτσι σε σημείο η ένταση είναι
όπου Ι0 η μέγιστη ένταση που εμφανίζεται στην εικόνα συμβολής.
Το πείραμα των δύο σχισμών του Young και το φαινόμενο της συμβολής αποτέλεσαν την ουσιαστικότερη επιβεβαίωση της κυματικής φύσης του φωτός. Από την απόσταση των φωτεινών ή των σκοτεινών κροσσών στο πέτασμα μπορούμε επίσης να υπολογίσουμε το μήκος κύματος της ακτινοβολίας.
4.4. Στάσιμα κύματα
Μία ειδική περίπτωση συμβολής κυμάτων είναι τα στάσιμα κύματα. Στάσιμα κύματα έχουμε όταν συμβάλουν δύο ίδια κύματα που οδεύουν σε αντίθετες κατευθύνσεις. Μπορούμε πολύ εύκολα να δημιουργήσουμε στάσιμα κύματα. Αρκεί να παρεμβάλουμε κάθετα στην διεύθυνση διάδοσης της ακτινοβολίας ένα κάτοπτρο. Τότε το κύμα θα ανακλαστεί στο κάτοπτρο και θα γυρίσει πίσω συμβάλλοντας με το αρχικό.
Στο σημείο αυτό θα πρέπει να αναφέρουμε ότι όταν ένα ηλεκτρομαγνητικό κύμα ανακλάται από την διαχωριστική επιφάνεια ενός πυκνότερου οπτικά μέσου σε σχέση με αυτό που διαδίδεται ή ενός αγωγού τότε το ανακλώμενο κύμα έχει διαφορά φάσης με το προσπίπτον 180°. Αν η διαχωριστική επιφάνεια είναι ενός οπτικά αραιότερου μέσου τότε δεν υφίσταται μεταβολή της φάσης.
Έστω λοιπόν ένα κύμα που ανακλάται κάθετα πάνω σε ένα κάτοπτρο. Οι κυματικές εξισώσεις του οδεύοντος και του ανακλώμενου είναι αντίστοιχα
|
|
(4.18) |
|
|
(4.19) |
όπου x η απόσταση από το κάτοπτρο. Το συνιστώμενο κύμα θα έχει εξίσωση
|
|
(4.20) |
Η σχέση αποτελεί την κυματοσυνάρτηση ενός στάσιμου κύματος. Παρατηρείστε ότι κάθε σημείο του χώρου ταλαντώνεται με ένα πάντα σταθερό πλάτος ΕS που είναι εξαρτάται από την απόσταση του σημείου από το κάτοπτρο
Όπως παρατηρούμε στην τελευταία σχέση υπάρχουν σημεία που ταλαντώνονται με μέγιστο πλάτος 2Εm, αλλά υπάρχουν και σημεία που το πλάτος ταλάντωσης είναι μηδενικό. Τα σημεία με το μέγιστο πλάτος ταλάντωσης λέγονται κοιλίες ή κορυφές του στάσιμου κύματος, ενώ τα σημεία μηδενικής ταλάντωσης λέγονται δεσμοί. Από την σχέση (4.21) βλέπουμε ότι κοιλίες έχουμε όταν το x είναι περιττό πολλαπλάσιο του λ/4 και δεσμούς έχουμε όταν είναι άρτιο πολλαπλάσιο το λ/4 ή ισοδύναμα όταν είναι πολλαπλάσιο του μισού του μήκους κύματος της ακτινοβολίας.
Η απόσταση μεταξύ δύο δεσμών αποτελεί το μήκος κύματος του στάσιμου κύματος και είναι ίση με το μισό του μήκους κύματος της ακτινοβολίας που δημιουργεί το στάσιμο κύμα, όπως βλέπουμε και στο Σχήμα 4.6.
4.5. Περίθλαση
Όταν τα κύματα φωτός περάσουν από μία μικρή οπή, στην άλλη πλευρά βλέπουμε εικόνες συμβολής αντί για μία απλή φωτεινή κηλίδα, όπως θα αναμέναμε με βάση την κλασική οπτική, να δημιουργήσει η οπή. Παρατηρούμε δηλαδή φως εκεί που “λογικά” θα περιμέναμε να υπάρχει σκιά. Το φαινόμενο είναι κοινό σε όλα τα είδη κυμάτων. Έτσι λοιπόν ακούμε ήχους γύρω από γωνίες δρόμων, παρατηρούμε κύματα μέσα σε λιμάνια που προστατεύονται από λιμενοβραχίονες κ.λ.π.
Ας πάρουμε ξανά το πείραμα των δύο σχισμών του Young που εξετάσαμε στην § 4.3. Έστω ότι στις δύο σχισμές πέφτει μία δέσμη φωτός. Αν το φως συνέχιζε να διαδίδεται ευθύγραμμα τότε δεν θα είχαμε υπέρθεση και συμβολή. Σύμφωνα όμως με την αρχή του Huygens κάθε σημείο της οπής δρα σαν δευτερεύουσα πηγή και εκπέμπει ένα σφαιρικό κύμα. Έτσι το φως παρακάμπτει την ευθύγραμμη διάδοση και οδεύει και σε περιοχές όπου αναμενόταν να υπάρχει σκοτάδι. Το φαινόμενο αυτό της εκτροπής από την κλασικά ευθύγραμμη διάδοση του φωτός λέγεται περίθλαση. Η περίθλαση λοιπόν είναι αποτέλεσμα συμβολής πολλών σύμφωνων πηγών κυμάτων.
Για να παρατηρήσουμε φαινόμενα περίθλασης θα πρέπει οι σχισμές ή τα εμπόδια να έχουν διαστάσεις της ίδιας τάξης μεγέθους με το μήκος κύματος της περιθλώμενης ακτινοβολίας.
Έχουμε δύο κατηγορίες φαινομένων περίθλασης. Την περίθλαση Fraunhofer και την περίθλαση Fresnel. Στην περίθλαση Fraunhofer, που είναι και η απλούστερη, υποθέτουμε ότι τόσο η προσπίπτουσα ακτινοβολία όσο και η περιθλώμενες ακτίνες που φτάνουν στο πέτασμα παρατήρησης είναι μεταξύ τους παράλληλες. Για να μπορέσουμε να έχουμε περίθλαση Fraunhofer ή θα πρέπει να τοποθετήσουμε την πηγή και το πέτασμα παρατήρησης αρκετά μακριά από το αντικείμενο (π.χ. την σχισμή) που δημιουργεί την περίθλαση ή θα πρέπει να χρησιμοποιήσουμε συγκλίνοντες φακούς οι οποίοι θα μετατρέψουν τις ακτίνες μας σε παράλληλες. Στη περίθλαση Fresnel οι ακτίνες δεν είναι παράλληλες με αποτέλεσμα η εικόνα περίθλασης να είναι αρκετά πολύπλοκη. Στις επόμενες λοιπόν παραγράφους θα μελετήσουμε μόνο την απλούστερη περίπτωση της περίθλασης Fraunhofer.
4.5.1. Περίθλαση από απλή σχισμή
Ας υποθέσουμε ότι μια δέσμη φωτός, μήκους κύματος λ, πέφτει πάνω σε ένα πέτασμα το οποίο έχει μια μικρή ορθογώνιο σχισμή πλάτους α πολύ μικρότερου από το μήκος της. Το πλάτος α της σχισμής είναι της τάξης του μήκους κύματος λ (π.χ. α=3λ).
Όπως βλέπουμε και στο Σχήμα 4.7 τα διάφορα σημεία της σχισμής δρουν σαν δευτερεύουσες πηγές κυμάτων, σύμφωνα με την αρχή του Huygens. Έτσι το φως σε ένα σημείο του χώρου μετά την σχισμή θα είναι αποτέλεσμα συμβολής όλων των κυμάτων από τις δευτερεύουσες πηγές.
Ας υποθέσουμε ότι σχισμή αποτελείται από πολλές σχισμές απειροελάχιστου πλάτους. Έστω λοιπόν ότι η κάθε απειροελάχιστου πλάτους σχισμή συνεισφέρει κύμα έντασης ΔΕ.
Από δύο σχισμές που απέχουν απόσταση y εκπέμπονται κύματα που συμβάλουν σε ένα σημείο του χώρου Ρ. Η ένταση από τις δύο σχισμές στο Ρ θα είναι σύμφωνα με την σχέση (4.11)
|
|
(4.22) |
Αν ολοκληρώσουμε για όλες τις σχισμές από y=0 έως y=α έχουμε την συνολική ένταση του ηλεκτρικού πεδίου στο Ρ
Ο συντελεστής 1/2 οφείλετε στο ότι στο ολοκλήρωμα παίρνουμε δύο φορές τις ίδιες περιοχές ( π.χ. μία φορά την συμβολή της 1 με την 3 και μία δεύτερη φορά της 3 με την 1)
Για γωνία θ=0 η σχέση (4.23) μας δίνει
|
|
(4.24) |
ενώ για μία οποιαδήποτε τυχαία γωνία θ
|
|
(4.25) |
Για την ένταση του φωτός έχουμε αντίστοιχα
Από την σχέση (4.26) βλέπουμε ότι η εικόνα της περίθλασης από απλή σχισμή αποτελείται από οριζόντιους κροσσούς συμβολής. Στην θέση θ=0 παρουσιάζεται ο φωτεινός κροσσός μηδενικής τάξης (βλέπε και Σχήμα 4.8). Σκοτεινοί κροσσοί παρουσιάζονται στις θέσεις που το Ι γίνεται μηδέν. Αυτό συμβαίνει όταν μηδενίζεται ο αριθμητής στην (4.26), δηλαδή όταν
όπου m = 1, 2, 3, 4… είναι ακέραιος αριθμός και ονομάζεται τάξη του σκοτεινού κροσσού.
Για να βρούμε τις θέσεις των φωτεινών κροσσών θα πρέπει να βρούμε για ποιες
τιμές της γωνίας εκτός αυτών της (4.27) μηδενίζεται η
παράγωγος της (4.26).
|
Σχήμα 4.8 Εικόνα συμβολής Fraunhofer από απλή σχισμή. Αριστερά : κατανομή της έντασης του φωτός. Δεξιά : οι φωτεινοί και σκοτεινοί κροσσοί της περίθλασης |
4.5.2. Περίθλαση από φράγμα σχισμών
Ας εξετάσουμε τώρα την περίπτωση που έχουμε ένα φράγμα το οποίο όμως περιέχει πολλές παράλληλες ορθογώνιες σχισμές. Τέτοια φράγματα λέγονται φράγματα περίθλασης. Είδαμε προηγουμένως ότι μία ορθογώνια σχισμή δημιουργεί μία εικόνα περίθλασης (Σχήμα 4.8). Στην περίπτωση των πολλών σχισμών κάθε σχισμή δημιουργεί την δικιά της εικόνα περίθλασης. Το τελικό αποτέλεσμα όλων των σχισμών προέρχεται από την συμβολή όλων των εικόνων περίθλασης των σχισμών.
Λόγω των πολύπλοκων μαθηματικών πράξεων θα δώσουμε χωρίς απόδειξη την εξίσωση της έντασης του περιθλώμενου φωτός από ένα φράγμα το οποίο αποτελείται από Ν το πλήθος, παράλληλες μεταξύ τους, ορθογώνιες σχισμές, που απέχουν μεταξύ τους απόσταση d και έχουν πλάτος α. Η ένταση, λοιπόν, του περιθλώμενου φωτός είναι
|
|
(4.28) |
Βλέπουμε δηλαδή ότι αποτελείται από τον γνωστό μας παράγοντα περίθλασης
|
|
(4.29) |
και τον παράγοντα συμβολής
|
|
(4.30) |
Η ένταση του φωτός μπορεί λοιπόν να γραφεί
|
|
(4.31) |
4.5.3. Περίθλαση από δύο σχισμές
Σαν εφαρμογή του φράγματος περίθλασης ας δούμε με λίγο περισσότερη λεπτομέρεια την περίπτωση Ν=2, δηλαδή ενός φράγματος από δύο σχισμές.
Για Ν=2 ο παράγοντας συμβολής γίνεται
όπου χρησιμοποιήσαμε την γνωστή τριγωνομετρική ταυτότητα sin(2x)=2sin(x)cos(x).
Η ένταση του φωτός, χρησιμοποιώντας την (4.32) γράφεται
Στο Σχήμα 4.9
παρουσιάζεται μία εικόνα περίθλασης από δύο σχισμές που η μεταξύ τους
απόσταση d δεκαπέντε μήκη κύματος και το πλάτος, α, της κάθε σχισμής είναι
τριπλάσιο του μήκους κύματος, λ.
Στο σημείο αυτό ας ξαναθυμηθούμε την § 4.3 όπου εξετάσαμε την περίπτωση της συμβολής του φωτός δύο φωτεινών πηγών. Είχαμε βρει ότι η ένταση του φωτός δίνεται από την σχέση (εξίσωση 4.17)
|
|
|
Τότε όμως είχαμε υποθέσει ότι η πηγές είναι σημειακές. Στην περίπτωση μας οι πηγές φωτός είναι δύο ορθογώνιες σχισμές, με άλλα λόγια έχουν διαστάσεις. Η ένταση, λοιπόν, κάθε σχισμής δεν είναι σταθερή, όπως στην περίπτωση των σημειακών πηγών, αλλά μεταβάλλεται λόγω περίθλασης σύμφωνα με την σχέση (4.26). Άρα το αποτέλεσμα της συμβολής διαμορφώνεται σύμφωνα με την εικόνα περίθλασης της σχισμής. Στο Σχήμα 4.10 παρουσιάζονται ο παράγοντας συμβολής, ο παράγοντας περίθλασης και η τελική μετρούμενη ένταση του φωτός σαν συνάρτηση της γωνίας θ, για την περίπτωση που το πλάτος, α, της κάθε σχισμής είναι τριπλάσιο του μήκους κύματος, λ, ενώ η απόσταση d των δύο σχισμών είναι δεκαπέντε μήκη κύματος. Η εικόνα περίθλασης αυτής της περίπτωσης παρουσιάστηκε στο Σχήμα 4.9. Η διακεκομμένη καμπύλη στο διάγραμμα της έντασης του φωτός είναι η καμπύλη του παράγοντα περίθλασης. Προσέξτε πως ο παράγοντας αυτός διαμορφώνει τα μέγιστα πλάτη της έντασης.
4.5.4. Περίθλαση από ακμή και από εμπόδιο.
Στην συνέχεια θα δούμε σε συντομία τις περιπτώσεις περίθλασης από μία ακμή και από ένα εμπόδιο (ένα αντικείμενο).
Για την περίπτωση της ακμής υποθέτουμε ότι το φως πέφτει πάνω σε ένα πλαίσιο του οποίου η μία πλευρά, η μία ακμή, βρίσκεται ακριβώς μπροστά από την δέσμη ενώ οι άλλες πλευρές είναι τόσο μακριά που θα μπορούσαμε να τις θεωρήσουμε ότι εκτείνονται στο άπειρο.
Όπως είναι πια φανερό, από όλα όσα αναφέραμε στις προηγούμενες σελίδες, το φως θα περιθλαστεί στην ακμή και πίσω από το πλαίσιο θα εμφανιστεί μία εικόνα συμβολής όπως αυτή του Σχήματος 4.11.
Κροσσοί περίθλασης εμφανίζονται στην περιοχή όπου θα περιμέναμε να υπάρχει μία ενιαία φωτεινή περιοχή. Στην περιοχή σε της σκιάς, όπου θα περιμέναμε να υπάρχει τέλεια σκιά, βλέπουμε να υπάρχει φως. Το φως δεν μειώνεται απότομα αλλά σταδιακά καθώς απομακρυνόμαστε από το σημείο ακριβώς μπροστά από την ακμή.
Η περίπτωση της περίθλασης από εμπόδιο παρουσιάζει ένα ιδιαίτερο ενδιαφέρον. Όταν πάνω σε ένα αντικείμενο, π.χ. ένα νόμισμα, πέφτει μία δέσμη φωτός τότε παρατηρείται εικόνα περίθλασης. Το Σχήμα 4.12 παρουσιάζει μία εικόνα περίθλασης από ένα κυκλικό αντικείμενο. Η εικόνα αποτελείται από κροσσούς στα άκρα της περιοχής που θα περιμέναμε να έχει σκιά. Το πιο εντυπωσιακό όμως σ΄ αυτή την περίπτωση είναι ότι στο κέντρο ακριβώς της σκιάς του αντικειμένου παρατηρείται μία φωτεινή κηλίδα!
Μετά από όσα αναφέραμε στις προηγούμενες σελίδες η εξήγηση της φωτεινής κηλίδας πρέπει να είναι προφανής. Ας πάρουμε δύο σημεία πάνω στην περιφέρεια του κυκλικού αντικειμένου. Τα δύο αυτά σημεία δρουν ως δευτερεύουσες πηγές κυμάτων οι οποίες είναι σύμφωνες. Τα κύματα από τα δύο αυτά σημεία συμβάλουν γενικά στον χώρο και η διαφορά φάσης τους είναι ίση με την διαφορά διαδρομής των κυμάτων από τις πηγές μέχρι το σημείο συμβολής. Αν τώρα εξετάσουμε την συμβολή ακριβώς πίσω από το κέντρο του αντικειμένου τότε βλέπουμε ότι οι διαδρομές (r1 και r2 στο Σχήμα 4.12) είναι ίσες, άρα η διαφορά διαδρομής είναι μηδέν. Βλέπουμε λοιπόν ότι ακριβώς πίσω από το κέντρο τα κύματα συμβάλουν ενισχυτικά και έτσι το σημείο αυτό εμφανίζεται πολύ φωτεινότερο από την γύρω περιοχή. Όταν ο Fresnel διατύπωσε την κυματική θεωρία του φωτός, ο Poisson, που ήταν εντελώς αντίθετος με την θεωρία αυτή, έλεγε ότι αν ο Fresnel είχε δίκαιο τότε στο κέντρο της σκιάς ενός αντικειμένου πρέπει να υπάρχει μία φωτεινή κηλίδα. Ο Poisson με αυτή του την υπόδειξη προσπαθούσε να καταρρίψει την θεωρία του Fresnel, μιας και τέτοια φωτεινή κηλίδα δεν είχε ως τότε παρατηρηθεί. Αργότερα όμως ο Arago, σε πειράματα που έκανε, παρατήρησε την φωτεινή αυτή κηλίδα. Έτσι ο Poisson, με την υπόδειξη του αυτή, στάθηκε αφορμή για την απόδειξη και όχι την κατάρριψη της κυματικής θεωρίας του φωτός.
5. Σωματιδιακή φύση του φωτός
5.1. Εισαγωγή
Στα προηγούμενα κεφάλαια είδαμε ότι το φως είναι ηλεκτρομαγνητικό κύμα και με βάση την κυματική θεωρία μπορέσαμε να εξηγήσουμε πλήρως διάφορα φαινόμενα όπως η συμβολή και η περίθλαση του φωτός. Ακόμη, φαινόμενα όπως η ανάκλαση και η διάθλαση μπορούν, χωρίς όμως να είναι απαραίτητο, να εξηγηθούν με την κυματική φύση του φωτός.
Υπάρχουν όμως και φαινόμενα των ηλεκτρομαγνητικών ακτινοβολιών που δεν είναι δυνατόν να εξηγηθούν με την υπόθεση ότι το φως είναι κύμα. Φαινόμενα όπως το φωτοηλεκτρικό φαινόμενο ή το φαινόμενο Compton, χρειάζονται μια διαφορετική αντιμετώπιση.
Στις αρχές του 20ου αιώνα μια νέα θεωρία προτάθηκε για το φως. Η θεωρία αυτή πρότεινε ότι το φως, ναι μεν είναι κύμα, αλλά ταυτόχρονα συμπεριφέρεται και σαν σωματίδιο. Στη συνέχεια θα παρουσιάσουμε τα δύο φαινόμενα που ενισχύουν την θεωρία περί της σωματιδιακής φύσης του φωτός καθώς και μερικά στοιχεία και εφαρμογές που έχουν σχέση με την σωματική φύση του φωτός και την κβαντική θεωρία της Φυσικής.
5.2. Φωτοηλεκτρικό φαινόμενο.
Ένα από τα φαινόμενα που μας οδήγησαν στην υιοθέτηση της σωματιδιακής θεωρίας του φωτός είναι το λεγόμενο φωτοηλεκτρικό φαινόμενο. Προς το τέλος του 19ου αιώνα ανακαλύφθηκε ότι όταν το φως πέσει πάνω σε ορισμένες μεταλλικές επιφάνειες, τότε από τις επιφάνειες αυτές εκπέμπονται ηλεκτρόνια. Τα ηλεκτρόνια αυτά ονομάζονται φωτοηλεκτρόνια. Το φαινόμενο το παρατήρησε πρώτος ο Hertz αλλά δεν μπόρεσε να το ερμηνεύσει ικανοποιητικά.
Στο Σχήμα 5.1 παρουσιάζεται μια απλοποιημένη εργαστηριακή εγκατάσταση για την παρατήρηση του πειράματος. Μια λυχνία που εσωτερικά έχει κενό αέρος έχει ένα διαφανές παράθυρο από το οποίο μπορεί να εισέλθει φως στο εσωτερικό της. Η λυχνία είναι συνδεδεμένη με πηγή συνεχούς ρεύματος έτσι ώστε στα άκρα την να παρουσιάζεται διαφορά δυναμικού.
Όταν η λυχνία είναι στο σκοτάδι το
ρεύμα στο κύκλωμα είναι μηδενικό. Μέσα στην λυχνία, αφού είναι κενή αέρος, δεν
υπάρχουν φορείς ηλεκτρικού φορτίου (ηλεκτρόνια ή ιόντα) για να κλείσουν το
κύκλωμα. Όταν η λυχνία φωτιστεί τότε το φως που εισέρχεται από το παράθυρο και
πέφτει πάνω στην κάθοδο έχει σαν αποτέλεσμα την εξαγωγή από την κάθοδο
ηλεκτρονίων. Τα ηλεκτρόνια αυτά εξάγονται από την κάθοδο με μία αρχική ταχύτητα
και λόγω της διαφοράς δυναμικού ανάμεσα στα δύο ηλεκτρόδια κατευθύνονται
προς την άνοδο. Έτσι το κύκλωμα κλείνει και διαρρέεται από ρεύμα έντασης Ι.
Τα ηλεκτρόνια της καθόδου, όταν πάνω τους πέσει ηλεκτρομαγνητική ακτινοβολία , απορροφούν ενέργεια από την ηλεκτρομαγνητική ακτινοβολία και ταλαντώνονται. Αν η ενέργεια που απορροφούν είναι μεγαλύτερη από την ενέργεια σύνδεσης που τα κρατάει στο υλικό της καθόδου τότε εξέρχονται από την κάθοδο. Η κινητική τους ενέργεια όταν εξέλθουν είναι ίση με την διαφορά της ενέργειας που απορρόφησαν μείον την ενέργεια σύνδεσης.
Η αντίσταση R είναι μία μεταβλητή αντίσταση. Μεταβάλλοντας την τιμή της μεταβάλουμε την τάση στους ακροδέκτες της λυχνίας. Στο Σχήμα 5.2 παρουσιάζεται η γραφική παράσταση της έντασης του ρεύματος σαν συνάρτηση της εφαρμοζόμενης τάσης. Παρατηρούμε ότι οι καμπύλες παρουσιάζουν τρία σημαντικά στοιχεία.
|
Σχήμα 5.2 Ένταση του ρεύματος συναρτήσει της τάσης που εφαρμόζεται στους ακροδέκτες της λυχνίας στο φωτοηλεκτρικό φαινόμενο. |
1. Όταν αυξάνουμε την τάση η ένταση του ρεύματος αυξάνει μέχρι μία τιμή. Η περαιτέρω αύξηση της τάσης δεν έχει κανένα αποτέλεσμα στην ένταση του ρεύματος. Προφανώς αυτό συμβαίνει γιατί όλα τα φωτοηλεκτρόνια κατευθύνονται και συλλαμβάνονται από την άνοδο. Έτσι παραπάνω αύξηση της τάσης δεν πρόκειται να φέρει περισσότερα φωτοηλεκτρόνια.
2. Η ένταση του ρεύματος εξαρτάται από την ένταση του φωτός που προσπίπτει στην κάθοδο. Περισσότερο φως έχει σαν αποτέλεσμα περισσότερα ηλεκτρόνια.
3. Αν εφαρμόσουμε στους ακροδέκτες της λυχνίας αρνητική τάση V πάλι λαμβάνουμε ένα μικρό ρεύμα. Εφαρμόζοντας αρνητική τάση η άνοδος απωθεί αντί να έλκει τα ηλεκτρόνια. Αν όμως η κινητική ενέργεια της οποία έχουν τα ηλεκτρόνια όταν εξάγονται από την κάθοδο είναι μεγαλύτερη από eV τότε ορισμένα ηλεκτρόνια καταφέρνουν να φτάσουν στην άνοδο δημιουργώντας ένα μικρό ρεύμα. Αν η εφαρμοζόμενη αρνητική τάση γίνει ίση ή μικρότερη από μία τιμή Vs, που ονομάζεται τάση αποκοπής, το ρεύμα μηδενίζεται. Προφανώς η μέγιστη κινητική ενέργεια που μπορούν να έχουν τα φωτοηλεκτρόνια είναι
Στην αρχή οι επιστήμονες προσπάθησαν να ερμηνεύσουν το φαινόμενο στηριζόμενοι στις αρχές της κυματικής θεωρίας. Κατέληξαν όμως ότι το φωτοηλεκτρικό φαινόμενο δεν μπορεί να ερμηνευτεί πλήρως από την κυματική θεωρία. Τα σημαντικότερα σημεία που δεν μπορούσαν να ερμηνεύσουν είναι :
1. Όταν η συχνότητα του φωτός με το οποίο φωτίζεται η κάθοδος γίνει μικρότερη από μία συγκεκριμένη συχνότητα, fc, την οποία ονομάζουμε οριακή συχνότητα ή συχνότητα κατωφλιού (cutoff frequency), δεν έχουμε ρεύμα στο κύκλωμα, ανεξάρτητα από το πόση τάση εφαρμόζουμε. Η εκπομπή, δηλαδή, των φωτοηλεκτρονίων σταματάει. Η τιμή της fc εξαρτάται μόνο από το υλικό της καθόδου. Με βάση την κυματική θεωρία, αν φωτίζαμε την κάθοδο με εντονότερο φως θα έπρεπε να είχαμε εκπομπή φωτοηλεκτρονίων μιας και εντονότερο φως σημαίνει περισσότερη προσπίπτουσα ενέργεια.
2. Όταν έχουμε εκπομπή φωτοηλεκτρονίων η ένταση του ρεύματος, δηλαδή ο αριθμός των φωτοηλεκτρονίων που εκπέμπονται στη μονάδα του χρόνου, αυξάνεται ανάλογα με την ένταση του προσπίπτοντος φωτός. Αλλά η τάση αποκοπής Vs, με άλλα λόγια η κινητική ενέργεια των φωτοηλεκτρονίων, είναι ανεξάρτητη από την ένταση του φωτός και εξαρτάται, για την ίδια κάθοδο, από την συχνότητα της ακτινοβολίας.
Ο Albert Einstein ήταν ο πρώτος που κατάφερε να ερμηνεύσει πλήρως το φωτοηλεκτρικό φαινόμενο, που τυραννούσε τους επιστήμονες της εποχής. Το 1905, την ίδια χρονιά που δημοσίευσε την περίφημη Ειδική Θεωρία της Σχετικότητος που έφερε επανάσταση στην Φυσική, διατύπωσε και την επιτυχή ερμηνεία του φωτοηλεκτρικού φαινομένου. Για την ερμηνεία του αυτή τιμήθηκε το 1921 με το Βραβείο Nobel (και όχι για την Θεωρία της Σχετικότητος όπως πολλοί πιστεύουν).
Ο Einstein, επεκτείνοντας τις κβαντικές ιδέες του Planck, πρότεινε ότι το φως και γενικά οι ηλεκτρομαγνητικές ακτινοβολίες δεν είναι ένα συνεχές κοινό κύμα, αλλά αποτελείται από μικρά κυματικά πακέτα, τα λεγόμενα κβάντα φωτός (light quanta) ή φωτόνια (photons), το κάθε ένα από τα οποία έχει ενέργεια ίση με
όπου h είναι η σταθερά του Planck που είναι ίση με h = 6,626 · 10-34 J·s. Η ενέργεια λοιπόν του φωτός δεν είναι ισοκατανεμημένη πάνω σε όλο το κύμα, αλλά συγκεντρώνεται στα μικρά πακέτα, τα φωτόνια.
Όταν το φως πέσει πάνω σε ένα υλικό τότε κάθε ηλεκτρόνιο απορροφά την ενέργεια ενός και μόνο ενός φωτονίου. Αν η ενέργεια του φωτονίου είναι μεγαλύτερη από την ενέργεια σύνδεσης Uc, ή όπως αλλιώς λέγεται, από το έργο εξαγωγής του ηλεκτρονίου, τότε το ηλεκτρόνιο αποδεσμεύεται από την κάθοδο με κινητική ενέργεια ίση με
Με την θεωρία αυτή των κβάντων φωτός τα σημεία που δεν μπορούσαν να ερμηνευτούν από την κυματική θεωρία βρήκαν την εξήγηση τους. Έτσι :
1. Όπως είναι φανερό από την σχέση (5.3) αν η συχνότητα f των φωτονίων είναι μικρότερη του έργου εξαγωγής Uc τότε δεν είναι δυνατή η εκπομπή φωτοηλεκτρονίων από την κάθοδο και το κύκλωμα δεν διαρρέεται από ρεύμα. Η ελάχιστη συχνότητα, η συχνότητα αποκοπής είναι ίση με
|
|
(5.4) |
όπως συνεπάγεται από την (5.3) θέτοντας Kmax=0. To έργο εξαγωγής, προφανώς, εξαρτάται μόνο από το υλικό της καθόδου και έχει σχέση με το πόσο ισχυρά συγκρατούν τα άτομα της καθόδου τα ηλεκτρόνια τους.
2. Προφανώς, μεγαλύτερη ένταση του φωτός σημαίνει περισσότερα φωτόνια, άρα και περισσότερα εκπεμπόμενα φωτοηλεκτρόνια. Η κινητική ενέργεια όμως των φωτοηλεκτρονίων, σύμφωνα με την σχέση (5.3), εξαρτάται μόνο από την συχνότητα του φωτός. Έτσι η τάση αποκοπής είναι ανεξάρτητη της έντασης του φωτός και εξαρτάται μόνο από την συχνότητα.
Η τελική επιβεβαίωση της θεωρίας του Einstein έγινε μετά από μετρήσεις της τάσης αποκοπής Vs σαν συνάρτηση της συχνότητας f. Από τις σχέσεις (5.1) και (5.3) έχουμε ότι
|
|
(5.5) |
Πράγματι αυτή η γραμμική σχέση μεταξύ της συχνότητας f και της τάσης αποκοπής Vs επιβεβαιώθηκε από τις μετρήσεις, οι οποίες έδειξαν ότι η κλίση της ευθείας είναι ίση με h/e.
5.3. Φαινόμενο Compton.
Ό Einstein για να εξηγήσει το φωτοηλεκτρικό φαινόμενο πρότεινε τα πακέτα φωτός, τα φωτόνια. Δεν χρειάστηκε όμως να ασχοληθεί με το αν τα φωτόνια είναι ή μάλλον συμπεριφέρονται ή όχι σαν σωματίδια. Αργότερα, το 1919, κατέληξε στο συμπέρασμα ότι τα φωτόνια διαδίδονται μόνο προς μία κατεύθυνση (ένα σφαιρικό κύμα αποτελείται από διαφορετικά φωτόνια που το καθένα διαδίδεται κατά μήκος μιας ακτίνας). Επίσης το κάθε φωτόνιο που μεταφέρει ενέργεια E έχει και ορμή ίση με Ε/c. Ο Compton και ανεξάρτητα ο Debye (η γνωστή “μάχη” αμερικανών και ευρωπαίων!) μελετώντας την σκέδαση των ακτίνων Χ από ηλεκτρόνια επέκτειναν τις ιδέες του Einstein δίνοντας στο φως και την σωματιδιακή φύση.
Ας δούμε λίγο πιο αναλυτικά το φαινόμενο της σκέδασης των ακτίνων Χ που προς τιμήν του Arthur Compton ονομάστηκε φαινόμενο Compton.
Στο Σχήμα 5.3 φαίνεται μία απλούστευση της πειραματικής συσκευής που χρησιμοποιήθηκε από τον Compton. Δέσμη ακτίνων Χ μήκους κύματος λ0 εκπέμπεται από την λυχνία και πέφτει πάνω σε ένα στόχο από γραφίτη. Εκεί η ακτινοβολία σκεδάζεται προς όλες τις κατευθύνσεις. Με ένα διάφραγμα επιλέγουμε την ακτινοβολία που σκεδάζεται κατά μία συγκεκριμένη γωνία θ. Η ακτινοβολία αναλύεται στα διάφορα μήκη κύματος από τα οποία αποτελείται, από έναν αναλυτή φάσματος και η ένταση της, σε κάθε μήκος κύματος, καταγράφεται από έναν ανιχνευτή ακτινοβολίας.
Η ακτίνες Χ πέφτοντας πάνω στον στόχο εξαναγκάζουν τα ηλεκτρόνια του στόχου σε ταλάντωση. Τα ταλαντούμενα ηλεκτρόνια εκπέμπουν με την σειρά τους ακτινοβολία με μικρότερη συχνότητα (μεγαλύτερο μήκος κύματος) Σύμφωνα με την κυματική θεωρία η εκπομπή της ακτινοβολίας από τα ηλεκτρόνια γίνεται προς όλες τις κατευθύνσεις και το μήκος κύματος εξαρτάται από την ένταση της προσπίπτουσας ακτινοβολίας και τον χρόνο έκθεσης του στόχου σ’ αυτήν. Ο Compton όμως παρατήρησε διαφορετικά αποτελέσματα!. Στο Σχήμα 5.4 παρουσιάζονται τέσσερις καμπύλες έντασης της σκεδασθείσας ακτινοβολίας στα διάφορα μήκη κύματος που αυτή αναλύεται. Κάθε καμπύλη αντιστοιχεί σε διαφορετική γωνία σκέδασης θ. Για θ=0, όπως βλέπουμε στην πάνω αριστερά καμπύλη, ανιχνεύεται μόνο η πρωτογενής ακτινοβολία μήκους κύματος λ0.
Στο σημείο αυτό ίσως γεννάται η
απορία γιατί αφού η πρωτογενής ακτινοβολία είναι μονοχρωματική με μήκος κύματος
λ0, στο σχήμα η καμπύλη της έντασης περιλαμβάνει και άλλες
συχνότητες αριστερά και δεξιά της λ0. Θεωρητικά, η ένταση, θα έπρεπε
να είναι παντού μηδέν και μόνο στην τιμή λ0 να εμφανίζεται μία
ευθεία γραμμή. Όπως θα λέγαμε στα μαθηματικά να είναι μία συνάρτηση δ. Αυτό
όμως ισχύει μόνο θεωρητικά. Στην πράξη υπεισέρχονται διάφορα φαινόμενα τα οποία
μεταβάλουν αυτό το θεωρητικό μοντέλο. Έτσι έχουμε σφάλματα στην μονάδα
ανίχνευσης. Κανένας ανιχνευτής δεν είναι απόλυτα ακριβής. Ας πάρουμε σαν
παράδειγμα ότι είμαστε σε ένα αυτοκίνητο και το ταχύμετρο δείχνει 100 km/h. Είμαστε σίγουροι ότι είναι 100 km/h και όχι 99.99 km/h και απλώς το ταχύμετρο επειδή δεν
έχει τόσες υποδιαιρέσεις μας δείχνει 100 km/h ; Επίσης, είναι σίγουρο, ότι η τάση
τροφοδοσίας της λυχνίας των ακτίνων Χ δεν είναι απόλυτα σταθερή. Αυτό έχει σαν
αποτέλεσμα η συχνότητα της ακτινοβολίας να “παίζει” λίγο. Τα φαινόμενα αυτά,
και δεν είναι μόνο αυτά τα δύο, έχουν σαν αποτέλεσμα η ένταση της ακτινοβολίας
να εμφανίζει μία διασπορά γύρω από την τιμή λ0. Η διασπορά έχει την
μορφή μιας κωδωνοειδούς καμπύλης. Αυτή η κωδωνοειδής καμπύλη ονομάζεται
κανονική κατανομή ή κατανομή Gauss και είναι της μορφής exp(-x2/σ2).
Έτσι λοιπόν δεν υπάρχει απόλυτα μονοχρωματική ακτινοβολία. Όσο όμως μικρότερη
είναι η διασπορά (το άνοιγμα) της καμπύλης τόσο πιο ακριβής είναι ο
χαρακτηρισμός μιας ακτινοβολίας ως μονοχρωματικής.
|
Σχήμα 5.4 Ένταση της σκεδασθείσας ακτινοβολίας σε διάφορα μήκη κύματος για διαφορετικές γωνίες σκέδασης θ. |
Ας ξαναγυρίσουμε όμως στο φαινόμενο Compton και στο Σχήμα 5.4. Βλέπουμε λοιπόν ότι για τις υπόλοιπες γωνίες σκέδασης θ (εκτός της θ=0) ανιχνεύεται εκτός της αρχικής ακτινοβολίας μήκους κύματος λ0 και μία δευτερεύουσα κορυφή σε ένα διαφορετικό για κάθε θ μήκος κύματος λ1. Το λ1 εξαρτάται μόνο από την γωνία σκέδασης. Η κορυφή λ0 οφείλεται στα ισχυρά συνδεδεμένα ηλεκτρόνια του στόχου που απορροφούν την ενέργεια της αρχικής ακτινοβολίας, ταλαντώνονται και επανεκπέμπουν ακτινοβολία στο ίδιο μήκος κύματος με την αρχική. Η κορυφή λ1 οφείλεται στα ελεύθερα ηλεκτρόνια του στόχου.
Ο Compton βρήκε ότι η διαφορά μήκους κύματος μεταξύ των δύο κορυφών εξαρτάται μόνο από την γωνία θ και είναι ίση με
όπου me η μάζα του ηλεκτρονίου, c η ταχύτητα του φωτός και h η σταθερή του Planck. Η διαφορά του μήκους κύματος για γωνία σκέδασης 90° ονομάζεται μήκος κύματος Compton λc και είναι ίσο με
Με βάση την κυματική οπτική τα παραπάνω αποτελέσματα του Compton ήταν ανεξήγητα. Το φαινόμενο μπορεί να εξηγηθεί αν δεχτούμε ότι το φως αποτελείται από φωτόνια. Κάθε φωτόνιο, όπως προαναφέραμε έχει ενέργεια
και μεταφέρει ορμή
|
|
(5.9) |
Το φωτόνιο συμπεριφέρεται σαν υλικό σωματίδιο. Όταν λοιπόν
πέσει πάνω σε ένα από τα ελεύθερα ηλεκτρόνια του στόχου τότε ισχύουν οι γνωστοί
νόμοι της κρούσης σωμάτων.
Στο Σχήμα 5.5 φαίνεται διαγραμματικά τι συμβαίνει κατά την σκέδαση Compton. Το φωτόνιο συγκρούεται με το ηλεκτρόνιο και μεταδίδει σ’ αυτό μέρος της ενέργειας και της ορμής του. Όπως ακριβώς συμβαίνει με τις μπάλες του μπιλιάρδου. Μετά την κρούση το φωτόνιο, που έχει μικρότερη συχνότητα μια και έδωσε ενέργεια στο ηλεκτρόνιο, εκτρέπεται από την αρχική του διεύθυνση κατά μία γωνία θ, την γωνία σκέδασης θ και το ανακρούον ηλεκτρόνιο κινείται προς μία άλλη διεύθυνση γωνίας φ με μια ταχύτητα υ. Η κυματική θεωρία προέβλεπε ότι το ηλεκτρόνιο θα έμενε στην ίδια θέση και θα εξέπεμπε ηλεκτρομαγνητικά κύματα προς όλες τις κατευθύνσεις όπως μία διπολική κεραία.
Όπως είναι γνωστό από την Μηχανική, κατά την κρούση ισχύουν οι αρχές διατήρησης της ενέργειας και διατήρησης της ορμής. Έτσι για την ενέργεια έχουμε .
|
Επριν = Εμετά |
(5.10) |
Πριν την κρούση, ενέργεια είχε μόνο το φωτόνιο. Η ενέργεια του φωτονίου δίνεται από την σχέση (5.8). Μετά την κρούση ενέργεια έχουν και το σκεδασθέν φωτόνιο και το ανακρούον ηλεκτρόνιο. Για ενέργεια του ηλεκτρονίου δεν πρέπει να χρησιμοποιήσουμε την κλασική σχέση ½ m υ2 γιατί η ταχύτητα υ του ηλεκτρονίου είναι συγκρίσιμη με την ταχύτητα του φωτός. Έτσι χρησιμοποιούμε την σχετικιστική έκφραση της κινητικής ενέργειας[1]
όπου το γ ο σχετικιστικός συντελεστής
|
|
|
Έτσι από την αρχή διατήρησης της ενέργειας έχουμε
Η ορμή του ηλεκτρονίου στην σχετικιστική της μορφή είναι
|
|
(5.13) |
Η αρχή διατήρησης της ορμής μας λέει ότι pπριν = pμετά. Αλλά ας μην ξεχνάμε ότι η ορμή είναι διάνυσμα και εφόσον διατηρείται σημαίνει ότι διατηρούνται ξεχωριστά και οι δύο συνιστώσες της (κατά την διεύθυνση διάδοσης του αρχικού φωτονίου, x, και κάθετα σ΄ αυτήν, y). Έτσι, λοιπόν, έχουμε
|
x διεύθυνση:
|
(5.14) |
Οι σχέσεις (5.12), (5.14) και (5.15) αποτελούν ένα σύστημα τριών εξισώσεων. Τα δύο στοιχεία που έχουν σχέση με το ηλεκτρόνιο, δηλαδή τα υ και φ, μας είναι άγνωστα αλλά μπορούν να απαλειφθούν.
Μετά από μερικές (όχι πολύ δύσκολες) αλγεβρικές πράξεις καταλήγουμε στην εξίσωση του Compton
5.4. Το φως, σωματίδιο ή κύμα ;
Από την εξέταση των δύο προηγουμένων φαινομένων έγινε φανερή η σωματιδιακή φύση του φωτός. Από την άλλη, στα δύο προηγούμενα κεφάλαια και ιδιαίτερα στο Κεφάλαιο 4 παρουσιάστηκε η κυματική του φύση. Είναι λοιπόν λογικό να γεννιέται το ερώτημα :
“Τελικά το φως τι είναι; Κύμα ή σωματίδιο;”
Η καλύτερη απάντηση στο ερώτημα είναι ότι το φως είναι φως! Κάτω από ορισμένες συνθήκες το βλέπουμε να συμπεριφέρεται σαν κύμα και κάτω από άλλες σαν σωματίδιο. Σε κάθε στιγμή είναι και τα δύο, απλώς δεν μπορούμε να το δούμε. Όλα εξαρτώνται από το μήκος κύματος.
Για να καταλάβουμε καλύτερα την τελευταία πρόταση ας συγκρίνουμε δύο ακτινοβολίες με πολύ διαφορετικό μήκος κύματος. Ας πάρουμε την περίπτωση της μικροκυματικής ακτινοβολίας με συχνότητα 10 GHz που αντιστοιχεί σε ένα μήκος κύματος περίπου 3 cm και των ακτίνων Χ με συχνότητα 1020 Ηz που αντιστοιχεί σε ένα μήκος κύματος περίπου 3 10-10 cm. Για να παρατηρήσουμε την περίθλαση των μικροκυμάτων χρειαζόμαστε σχισμές ή αντικείμενα με διαστάσεις της τάξης των 5-10 cm. Για την περίπτωση των ακτίνων Χ οι σχισμές πρέπει να είναι περίπου 10-7 cm. Όπως καταλαβαίνετε είναι πολύ απλό να παρατηρήσουμε την περίθλαση των μικροκυμάτων και να δούμε την κυματική φύση του φωτός, μιας και αντικείμενα μεγέθους μερικών εκατοστών είναι κάτι πολύ συνηθισμένο. Από την άλλη για να παρατηρήσουμε περίθλαση στις ακτίνες Χ χρειαζόμαστε σχισμές πλάτους 10-9 εκατοστά, (0.000000001 εκατοστά!) που προφανώς δεν είναι ΑΔΥΝΑΤΟΝ να κατασκευαστούν. Για να γίνει κατανοητό γιατί το αδύνατον τονίστηκε τόσο, λάβετε υπόψη ότι η ακτίνα ενός ατόμου είναι 10-8 cm!
Ας δούμε όμως τι συμβαίνει με την ανίχνευση της σωματιδιακής φύσης του φωτός. Η ενέργεια ενός φωτονίου των μικροκυμάτων είναι E = h f = 6,626 · 10-34 J·s · 1010 Hz = 6,626 10-24 J και μεταφέρουν ορμή περίπου ίση με E/c = 2,2 10-16 kg m/s. Οι ακτίνες Χ εφόσον έχουν 10.000.000.000 φορές μεγαλύτερη συχνότητα (1020 Hz) από τα μικροκύματα (1010 Hz) θα έχουν 10.000.000.000 φορές περισσότερη ενέργεια και ορμή. Για να παρατηρηθεί το φωτοηλεκτρικό φαινόμενο θα πρέπει η ενέργεια της ακτινοβολίας να είναι μεγαλύτερη από το έργο εξαγωγής των φωτοηλεκτρονίων. Το έργο εξαγωγής των φωτοηλεκτρονίων εξαρτάται, όπως είπαμε, από το υλικό της καθόδου, χοντρικά όμως είναι της τάξης των 10-19 J. Βλέπουμε λοιπόν πως τα μικροκύματα δεν μπορούν να προκαλέσουν φωτοηλεκτρικό φαινόμενο όχι γιατί δεν αποτελούνται από φωτόνια, αλλά επειδή η ενέργεια τους (της τάξης των 10-24 J) είναι πολύ μικρότερη του έργου εξαγωγής. Αντίθετα οι ακτίνες Χ έχουν πολύ μεγαλύτερη ενέργεια (της τάξης των 10-14 J) από το έργο εξαγωγής.
Η περίπτωση του φαινόμενου Compton επίσης δεν μπορεί να παρατηρηθεί στα μικροκύματα. Ας πάρουμε την περίπτωση της σκέδασης κατά 90°. Η διαφορά των μηκών κύματος, όπως είδαμε στις σχέσεις (5.6) και (5.7), είναι 0.0243 Ǻ που είναι ίσο με 2,43 10-10 cm. Όταν το μήκος κύματος είναι 3 cm όπως στην περίπτωση των μικροκυμάτων αυτή η απειροελάχιστη διαφορά είναι τελείως αδύνατον να μετρηθεί. Ποιο όργανο μπορεί να καταλάβει την διαφορά μεταξύ του 3 και του 3,000000000243;! Αντίθετα στις ακτίνες Χ, που το μήκος κύματος είναι 3 10-10 cm η διαφορά είναι ίση περίπου με το μήκος κύματος.
Έτσι λοιπόν καταλήγουμε ότι το φως είναι φως και πάντα συμπεριφέρεται και σαν κύμα και σαν σωματίδιο. Απλώς εμείς μπορούμε να ανιχνεύσουμε είτε την κυματική του φύση όταν η συχνότητα είναι μικρή είτε την σωματιδιακή του φύση όταν η συχνότητα είναι μεγάλη.
5.5. Απορρόφηση και εκπομπή ακτινοβολίας από την ύλη.
Αρκετές φορές στο παρόν αλλά και σε προηγούμενα κεφάλαια αναφέραμε ότι η ύλη απορροφά την ακτινοβολία και άλλες φορές την επανεκπέμπει, σε ίδιο ή διαφορετικό μήκος κύματος ενώ άλλες φορές η ακτινοβολία “εξαφανίζεται”. Δεν αναφερθήκαμε όμως μέχρι τώρα πιο αναλυτικά στα φαινόμενα εκπομπής και απορρόφησης γιατί έπρεπε πρώτα να αποκτήσουμε μια σαφή εικόνα για την φύση του φωτός. Η ακτινοβολία μπορεί να απορροφηθεί από την ύλη με διάφορους τρόπους. Απορρόφηση μπορεί να γίνει είτε από τα άτομα είτε και από τα μόρια της ύλης.
Πριν δούμε πως απορροφά και εκπέμπει ακτινοβολία ένα άτομο ας θυμηθούμε ορισμένα βασικά στοιχεία από την δομή των ατόμων.
Στην απλούστερη προσέγγιση του Bohr, ένα άτομο αποτελείται από τον πυρήνα γύρω από τον οποίο περιστρέφονται τα ηλεκτρόνια. Τα ηλεκτρόνια δεν βρίσκονται σε οποιαδήποτε θέση αλλά κατατάσσονται σε συγκεκριμένες στιβάδες όπως φαίνεται και στο Σχήμα 5.6. Κάθε στοιβάδα έχει την δικιά της, μοναδική, ενέργεια. Για το άτομο του υδρογόνου η ενέργεια της πρώτης, ή όπως αλλιώς λέγεται, της βασικής στοιβάδας (n=1) είναι
E1 = -13.6 eV.
To eV (ηλεκτρονιοβόλτ) είναι μονάδα ενέργεια (έργου) και ισοδυναμεί με 1,6 10-19 J. Για τις υπόλοιπες η ενέργεια δίνεται από την σχέση
|
|
(5.17) |
Παρατηρήστε ότι οι ενέργειες είναι αρνητικές και όσο πηγαίνουμε σε υψηλότερες στοιβάδες γίνονται μεγαλύτερες. Το ότι είναι αρνητικές σημαίνει ότι τα ηλεκτρόνια είναι δεσμευμένα στο άτομο και για να απομακρυνθούν πρέπει με κάποιο τρόπο να πάρουν ενέργεια. Αυτές οι διακριτές τιμές της ενέργειας λέγονται ενεργειακές στάθμες. Όταν ένα άτομο έχει όλα τα ηλεκτρόνια του στις χαμηλότερες ενεργειακές στάθμες έτσι ώστε η ενέργεια του να είναι η μικρότερη δυνατή τότε λέμε ότι βρίσκεται στην βασική ή θεμελιώδη κατάσταση. Κάθε άλλη κατάσταση ονομάζεται διεγερμένη.
Όταν ένα φωτόνιο πέσει πάνω σε ένα άτομο που βρίσκεται στην βασική κατάσταση τότε αν η ενέργεια του φωτονίου είναι ίση με την ενεργειακή διαφορά μεταξύ της βασικής και μιας διεγερμένης κατάστασης, το φωτόνιο απορροφάται από το ηλεκτρόνιο και το ηλεκτρόνιο μεταπηδά στην ανώτερη στοιβάδα (Σχήμα 5.7). Έστω για παράδειγμα το άτομο του υδρογόνου με το ηλεκτρόνιο στην θεμελιώδη κατάσταση Ε1. Αν πάνω του πέσει φωτόνιο με ενέργεια ίση με την ενεργειακή διαφορά της στάθμης n=3 από την στάθμη n=1, δηλαδή Ε3-Ε1=(-1,51 eV)-(-13,6 eV) = 12,09 eV τότε το φωτόνιο απορροφάται και το ηλεκτρόνιο ανεβαίνει στην στοιβάδα n=3. To ηλεκτρόνιο δεν μένει στην στοιβάδα αυτή για πολύ χρόνο. Ο χρόνος παραμονής είναι της τάξης των 10-8 s. Κατόπιν το ηλεκτρόνιο μεταπίπτει αυθόρμητα είτε απευθείας με ένα βήμα στην βασική στοιβάδα είτε με πολλά βήματα σε ενδιάμεσες χαμηλότερες στοιβάδες για να καταλήξει τελικά και πάλι στην βασική. Η αποδιέγερση αυτή συνοδεύεται από την εκπομπή ενός ή περισσοτέρων φωτονίων, ανάλογα αν η αποδιέγερση έγινε σε ένα ή περισσότερα βήματα. Η ενέργεια του εκπεμπόμενου φωτονίου είναι ίση με την ενεργειακή διαφορά της μετάπτωσης. Έτσι για την περίπτωση της αποδιέγερσης που απεικονίζεται στο Σχήμα 5.7 θα εκπεμφθούν δύο φωτόνια. Το ένα φωτόνιο θα έχει ενέργεια ίση με Ε3 - Ε2 = 1.89 eV και το δεύτερο ίση με Ε2 - Ε1 = 10.2 eV. Όπως είναι φυσικό (και επιτάσσει η αρχή διατήρησης της ενέργειας) τα δύο εκπεμπόμενα φωτόνια έχουν συνολική ενέργεια ίση με την ενέργεια του φωτονίου που απορροφήθηκε.
Αν το προσπίπτον φωτόνιο έχει μεγαλύτερη ενέργεια από την, κατ΄ απόλυτη τιμή, ενέργεια της θεμελιώδους κατάστασης, δηλαδή
|
|
(5.18) |
τότε το ηλεκτρόνιο αποδεσμεύεται από το άτομο έχοντας κινητική ενέργεια ίση με τη διαφορά Ep - ½E1½ και το άτομο εμφανίζεται ιονισμένο.
Εκτός της απορρόφησης ακτινοβολίας, διέγερση ενός ατόμου μπορεί να γίνει και από την σύγκρουση του με κάποιο σωματίδιο, όπως για παράδειγμα ένα ελεύθερο ηλεκτρόνιο. Μέρος της κινητικής ενέργειας του σωματιδίου μεταφέρεται στο ηλεκτρόνιο του ατόμου αναγκάζοντας του να μεταπηδήσει σε στοιβάδα μεγαλύτερης ενέργειας. Φυσικά, όπως και πριν, το ηλεκτρόνια, μετά από ελάχιστο χρόνο, θα μεταπέσει στην βασική του κατάσταση εκπέμποντας ένα ή περισσότερα φωτόνια ανάλογα με τα βήματα της μετάπτωσης. Στον μηχανισμό αυτό διέγερσης ατόμων και εκπομπής φωτονίων οφείλεται το λαμπρό φως των αστραπών και κεραυνών καθώς και η λειτουργία των λαμπτήρων φθορισμού. Στον κεραυνό έχουμε μία ξαφνική κίνηση των ηλεκτρονίων από τα φορτισμένα σύννεφα προς το έδαφος της γης. Τα ηλεκτρόνια κατά την βίαιη κάθοδο του συγκρούονται με τα άτομα του αέρα διεγείροντας τα. Τα άτομα αποδιεγείρονται με ταυτόχρονη εκπομπή φωτονίων.
Εκτός από τα δεσμευμένα ηλεκτρόνια των ατόμων ακτινοβολία μπορούν να απορροφήσουν και τα ελεύθερα ηλεκτρόνια των μετάλλων. Τα ηλεκτρόνια αυτά εφόσον είναι ελεύθερα απορροφούν φωτόνια οποιασδήποτε ενέργεια. Μέρος της ενέργειας που απορροφάται δίδεται σαν κινητική ενέργεια ανάκρουσης του ηλεκτρονίου (φαινόμενο Compton) ενώ η υπόλοιπη εξαναγκάζει το ηλεκτρόνιο σε ταλάντωση. Το ταλαντούμενο ηλεκτρόνιο εκπέμπει με την σειρά του ηλεκτρομαγνητική ακτινοβολία προς μία τυχαία διεύθυνση. Η εκπεμπόμενη ακτινοβολία έχει φυσικά μικρότερη συχνότητα από το φωτόνιο που απορροφήθηκε, μια και μέρος της αρχικής ενέργειας χρησιμοποιήθηκε σαν ενέργεια ανάκρουσης του ηλεκτρονίου.
Στο φαινόμενο αυτό οφείλεται η ανάκλαση των μικροκυμάτων και η απορρόφηση των ακτίνων Χ από τις μεταλλικές επιφάνειες. Στα μικροκύματα ένα φωτόνιο απορροφάται από ένα ελεύθερο ηλεκτρόνιο. Η ενέργεια των μικροκυμάτων είναι πολύ μικρή για να απορροφηθούν από τα ηλεκτρόνια των ατόμων και να διεγείρουν το άτομο. Το ηλεκτρόνιο επανεκπέμπει φωτόνιο μεγαλύτερου μήκους κύματος προς τυχαία διεύθυνση. Όπως όμως αναφέραμε στην § 5.4 η διαφορά του μήκους κύματος του νέου φωτονίου από το παλαιό είναι για τα μικροκύματα ελάχιστη. Έτσι πρακτικά η απώλεια ενέργειας είναι αμελητέα και το νέο φωτόνιο έχει πρακτικά την ίδια συχνότητα με το παλαιό. Αν το νέο φωτόνιο εκπεμφθεί προς το εσωτερικό του μετάλλου τότε είναι πολύ πιθανόν, σχεδόν σίγουρο μια και το μέταλλο έχει πάρα πολλά ελεύθερα ηλεκτρόνια, να συγκρουστεί με άλλο ηλεκτρόνιο και η διαδικασία να επαναληφθεί (Σχήμα 5.8). Ας μην ξεχνάμε ότι τα φορτία, τα ελεύθερα ηλεκτρόνια δηλαδή, συγκεντρώνονται στην εξωτερική επιφάνεια των αγωγών λόγω των ισχυρών απωστικών δυνάμεων Coulomb. Έτσι η πυκνότητα των ηλεκτρονίων στην “επιδερμίδα” του μετάλλου είναι πολύ μεγάλη αυξάνοντας έτσι την πιθανότητα διαδοχικών απορροφήσεων και επανεκπομπών. Έτσι τα φωτόνια δεν διαχέονται πολύ προς το εσωτερικό του μετάλλου και η ακτινοβολία εμφανίζεται να “ανακλάται”.
Στα παραπάνω υποθέσαμε ότι το νέο φωτόνιο
εκπέμπεται προς τυχαία διεύθυνση. Αυτό όμως δεν είναι απόλυτα σωστό. Λόγω των
απωστικών δυνάμεων Coulomb μεταξύ των ηλεκτρονίων που τα αναγκάζουν να συγκεντρώνονται
στη επιφάνεια του μετάλλου, το ανακρούον ηλεκτρόνιο δεν μπορεί να κινηθεί
εύκολα προς το εσωτερικό του μετάλλου. Έτσι λόγω της αρχής διατήρησης της ορμής
το νέο φωτόνιο που εκπέμπεται έχει πολύ μικρή πιθανότητα να κατευθύνεται προς
το εσωτερικό του μετάλλου.
Αντίθετα στις ακτίνες Χ η ορμή των φωτονίων είναι μεγάλη επιτρέποντας την κίνηση του ανακρούοντος ηλεκτρονίου προς το εσωτερικό. Η μεταβολή όμως του μήκους κύματος είναι σημαντικότατη με αποτέλεσμα το νέο φωτόνιο να χάνει σημαντική ενέργεια. Μετά από μερικές επαναλήψεις του φαινομένου σύγκρουσης-εκπομπής τα φωτόνια έχουν εξασθενήσει σημαντικά. Έτσι το μέταλλο φαίνεται να απορροφά τις ακτίνες Χ.
Απορρόφηση ακτινοβολίας μπορούμε να έχουμε και από τα μόρια. Ιονισμένα μόρια (ιόντα) αντιδρούν όπως τα ελεύθερα ηλεκτρόνια. Λόγω του φορτίου που έχουν εξαναγκάζονται σε ταλάντωση απορροφώντας την ηλεκτρομαγνητική ακτινοβολία. Το ίδιο συμβαίνει και με τα ουδέτερα μόρια τα οποία δεν έχουν συμμετρική κατανομή των φορτίων τους και παρουσιάζουν ηλεκτρική διπολική ροπή. Το μόριο του νερού (Σχήμα 5.9) είναι ένα τέτοιο μόριο. Τα μόρια αυτά μπορούν να απορροφήσουν ακτινοβολία που τα θέτει είτε σε περιστροφή ή και σε ταλάντωση των δεσμών των ατόμων τους. Κάθε δεσμός έχει την δικιά του ιδιοσυχνότητα ταλάντωσης. Με άλλα λόγια απορροφά συγκεκριμένη συχνότητα ακτινοβολίας. Η απορρόφηση της ακτινοβολίας από τα μόρια αυξάνει την κινητική τους ενέργεια. Ως γνωστόν η θερμοκρασία ενός σώματος είναι ένα μέτρο της κινητικής ενέργειας των μορίων του. Έτσι η αύξηση της κινητικής ενέργειας εκδηλώνεται με την αύξηση της θερμοκρασίας του σώματος. Στο φαινόμενο αυτό οφείλεται η απορρόφηση των μικροκυμάτων από το νερό. Έτσι σ’ ένα φούρνο μικροκυμάτων το νερό απορροφά την μικροκυματική ακτινοβολία και θερμαίνεται ενώ το πιάτο δεν μπορεί να απορροφήσει ακτινοβολία και παραμένει κρύο.
5.6. Φωτοδίοδοι (LED)
Ως γνωστόν, μία δίοδος αποτελείται από δύο ημιαγωγούς που βρίσκονται σε επαφή. Ο ένας ημιαγωγός είναι τύπου n και έχει περίσσια ηλεκτρονίων ενώ ο δεύτερος είναι τύπου p και στον οποίο περισσεύουν οι οπές. Όταν στα άκρα της διόδου εφαρμοστεί κατάλληλη τάση τότε τα ηλεκτρόνια και οι οπές μετακινούνται προς τα αντίστοιχα άκρα διαπερνώντας την διαχωριστική επιφάνεια των δύο ημιαγωγών (Σχήμα 5.10). Υπενθυμίζουμε ότι οι οπές δεν είναι τίποτα άλλο παρά άτομα τα οποία έχουν ιονιστεί χάνοντας ένα ηλεκτρόνιο.
Όταν τα ηλεκτρόνια διαπερνούν την διαχωριστική επιφάνεια επανασυνδέονται με τις οπές. Τα ηλεκτρόνια από την ζώνη αγωγιμότητας μεταπίπτουν στην ζώνη σθένους (που είναι και η βασική κατάσταση του ατόμου). Στα περισσότερα ημιαγωγικά υλικά αυτή η μετάπτωση γίνεται με ενδιάμεσα βήματα σε ανώτερες στοιβάδες. Έτσι εκπέμπονται φωτόνια με μικρή συχνότητα και η ακτινοβολία είναι θερμική (στην περιοχή του υπέρυθρου). Σε ορισμένα όμως υλικά, όπως το GaAs, η μετάπτωση αυτή στην στοιβάδα σθένους γίνεται σε ένα βήμα με ταυτόχρονη εκπομπή φωτονίων στο ορατό μήκος κύματος. Οι επανασυνδέσεις γίνονται κοντά στην επαφή και η ένταση του φωτός αυξάνει με την αύξηση του ρεύματος της διόδου (περισσότερα ηλεκτρόνια περνούν την επαφή και επανασυνδέονται με τις οπές). Μία τέτοια δίοδος ονομάζεται φωτοδίοδος ή όπως έχει επικρατήσει LED από τα αρχικά των λέξεων Light Emitting Diode (δίοδος που εκπέμπει φως).
Οι φωτοδίοδοι χρησιμοποιούνται συνήθως ως ενδεικτικές λυχνίες στις ηλεκτρικές και ηλεκτρονικές συσκευές και για την κατασκευή φωτεινών στοιχείων σε ηλεκτρονικά όργανα, μικρές επιγραφές, παιγνίδια κ.λ.π. Λόγω της μονοχρωματικής ακτινοβολίας που εκπέμπουν τελευταία χρησιμοποιούνται και για μετάδοση πληροφοριών μέσω οπτικών ινών, καθώς και στην κατασκευή laser ημιαγωγών.
5.7. Φωτοστοιχεία
Τα φωτοβολταϊκά στοιχεία ή όπως συνήθως ονομάζονται φωτοστοιχεία είναι διατάξεις που απορροφούν το φως και το μετατρέπουν σε ηλεκτρική ενέργεια. Η λειτουργία τους στηρίζεται στο ακριβώς αντίθετο φαινόμενο με την λειτουργία των LED. Όταν ένας ημιαγωγός απορροφά ακτινοβολία τα ηλεκτρόνια που βρίσκονται στην ζώνη σθένους απορροφούν την ενέργεια των φωτονίων και μεταπηδούν στην ζώνη αγωγιμότητας. Έτσι στον ημιαγωγό εμφανίζονται αρνητικοί (ηλεκτρόνια) και θετικοί (οπές) φορείς ηλεκτρικού φορτίου.
Αν ο ημιαγωγός είναι απομονωμένος τα ηλεκτρόνια επανασυνδέονται με τις οπές
εκπέμποντας ακτινοβολία. Αν αντίθετα ο ημιαγωγός είναι συνδεδεμένος σε κύκλωμα
και υπάρχει στα άκρα του διαφορά δυναμικού τότε ο ημιαγωγός διαρρέεται από
ρεύμα. Όπως είναι φυσικό, στον ημιαγωγό θα υπάρχουν περισσότεροι φορείς
ηλεκτρικού φορτίου όσο πιο έντονη είναι η ακτινοβολία του προσπίπτοντος φωτός.
Η δημιουργία περισσότερων φορέων έχει σαν αποτέλεσμα την αύξηση του ρεύματος
που διαρρέει τον ημιαγωγό.
Η παραπάνω διεργασία δεν μας προσφέρει όμως ενέργεια. Θα πρέπει να βρεθεί ένας τρόπος έτσι ώστε να εμποδίσουμε την επανασύνδεση των ηλεκτρονίων με τις οπές. Αυτό επιτυγχάνεται με χρήση δύο ημιαγωγών, ενός τύπου p και ενός τύπου n. Στο Σχήμα 5.11 παρουσιάζεται ένας φωτοστοιχείο ημιαγωγών πυριτίου με προσμίξεις φωσφόρου (τύπου n) και βαρίου (τύπου p). Το στρώμα του ημιαγωγού τύπου n είναι αρκετά λεπτό επιτρέποντας τα φωτόνια να το διαπεράσουν και να εισχωρήσουν στον ημιαγωγό τύπου p. Τα φωτόνια απορροφώνται από τα άτομα του ημιαγωγού δημιουργώντας ηλεκτρόνια και οπές. Τα ηλεκτρόνια αν παραμείνουν στον ημιαγωγό τύπου p θα επανασυνδεθούν όπως είπαμε με τις οπές. Επειδή όμως η δημιουργία ζευγών ηλεκτρονίων-οπών γίνεται κοντά στην επαφή p-n, αρκετά ηλεκτρόνια διαχέονται μέσω της επαφής στην περιοχή n. Η περιοχή n έχει έλλειψη οπών οπότε η επανασύνδεση των ηλεκτρονίων με οπές στην περιοχή αυτή είναι σπάνια. Έτσι στην περιοχή n συγκεντρώνονται αρνητικά φορτία ενώ στην περιοχή p παραμένουν οι οπές και εμφανίζεται φορτισμένη θετικά. Στους ακροδέκτες λοιπόν του φωτοστοιχείου εμφανίζεται διαφορά δυναμικού V.
Για την βελτίωση της απόδοσης και την ελαχιστοποίηση των ανακλάσεων η πάνω επιφάνεια του φωτοστοιχείο βάφεται με κατάλληλο υλικό. Η απόδοση ενός φωτοστοιχείου είναι σήμερα περίπου 1-1,5 V. Παρόλη την μικρή απόδοση η χρήση τους είναι πολύ σημαντική. Συνδεδεμένα σε σειρά ή παράλληλα μπορούν να καλύψουν της ανάγκες μικρών συσκευών. Για την κάλυψη μεγάλων αναγκών η χρήση τους δεν είναι ακόμη συμφέρουσα λόγω του υψηλού κόστους κατασκευής, παρόλο που το κόστος λειτουργίας τους είναι μηδενικό. Χρησιμοποιούνται όμως εκεί που η χρήση άλλων πηγών ενέργειας είναι δύσκολη έως αδύνατοι. Για παράδειγμα οι δορυφόροι και τα διαστημόπλοια χρησιμοποιούν μεγάλες συστοιχίες φωτοστοιχείων για την κάλυψη των ενεργειακών τους αναγκών. Μην ξεχνάμε ότι η μεταφορά καυσίμων στο διάστημα είναι αρκετά δύσκολη και τα καύσιμα αυτά κάποτε εξαντλούνται. Αντίθετα η ηλιακή ενέργεια είναι ανεξάντλητη.
ΒΙΒΛΙΟΓΡΑΦΙΑ
Breidenbach, K., “Experiments with Microwaves”, 1994, Leybold Didactic GmbH, Germany.
Griffiths, D., “Introduction to electrodynamics”, 1997, Prentice-Hall, Ελληνική μετάφραση / επιμέλεια Δήτσας Π., Κουρκουμέλη Χ., Πανεπιστημιακές Εκδόσεις Κρήτης.
Hewitt, P., “Conceptual Physics, Volume II”, 1985,
Ελληνική μετάφραση Σηφάκης Ε., 1997, Πανεπιστημιακές Εκδόσεις Κρήτης.
Schwartz, M., “Principles of Electrodynamics”, 1982, McGraw-Hill Ελληνική μετάφραση Παπαδημητράκη-Χλίχλια Ε., Τσουκαλάς Ι., Εκδόσεις Α.Π.Θ.
Serway, R., “Physics for Scientist and Engineers”, 1990, Sounders College Publishing, Ελληνική μετάφραση Ρεσβάνης Λ., εκδόσεις Γ. Κορφιάτη
Καρύμπακα, Κ. Α., “Γενική Ηλεκτρονική”, 1984, Εκδόσεις Ζήτη
Μανουσάκη, Γ.Ε., “Γενική και ανόργανη Χημεία”, 1983, Εκδόσεις Κυριακίδη.
Οικονόμου, Ν.Α., “Εισαγωγή στην Φυσική”, 1982, Εκδόσεις Α.Π.Θ.
Σιάπκα, Δ., Αγοραστού, Θ., Γεωργιάδου, Χ., Κουτσουμπέλη, Β., “Εισαγωγή στα Οπτικοηλεκτρονικά”, 1977, Εκδόσεις Α.Π.Θ.
Σπυριδέλη, Ι., “Θέματα οπτικής”, 1983, Εκδόσεις Α.Π.Θ.
Χαραλάμπους, Σ., “Εισαγωγή στην Ατομική και Μοριακή Φυσική”, 1981, Εκδόσεις Ζήτη.
[1] Η σχέση (5.11) μετατρέπεται στην κλασική έκφραση της κινητικής ενέργεια όταν η ταχύτητα υ είναι πολύ μικρότερη της c. Έτσι όταν υ/c ® 0 μπορούμε να αναπτύξουμε το γ σε σειρά Taylor ως προς υ/c, γύρω από την θέση υ/c=0. Για απλοποίηση των σχέσεων θέτουμε υ/c=z
|
|
|
Κρατώντας όρους μέχρι z2 και θέτοντας ξανά πίσω τα υ/c, το γ γίνεται
|
|
|
και η κινητική ενέργεια (5.11) μετατρέπεται στην κλασική της έκφραση
|
|
|
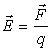


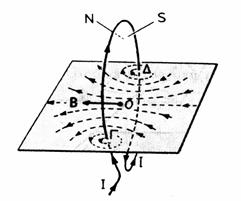
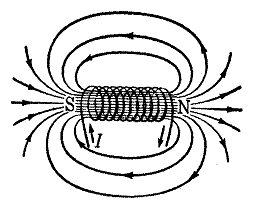


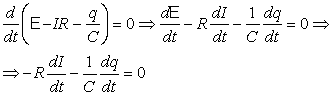
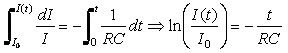
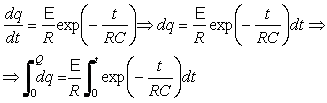
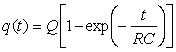



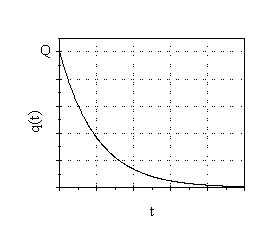






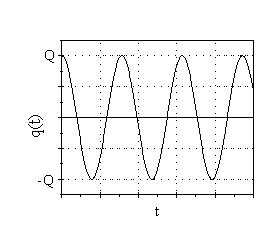



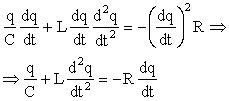
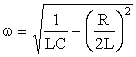

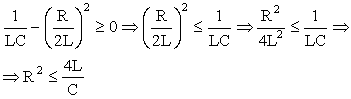


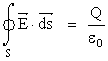
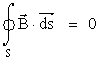
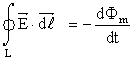
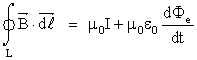
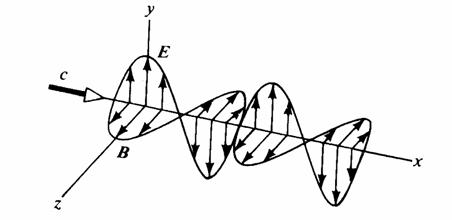
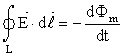
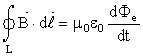
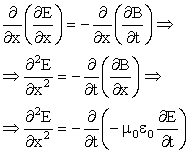
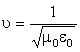
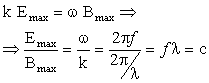
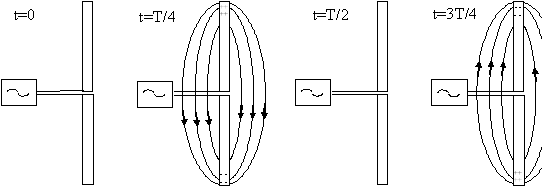
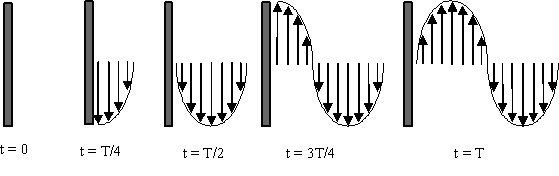
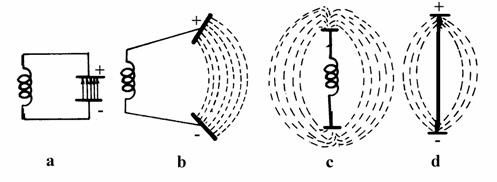
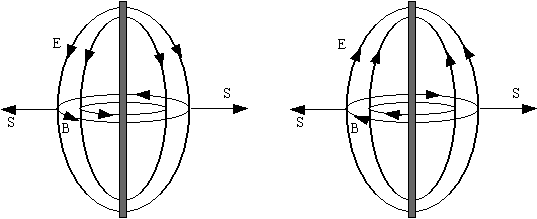
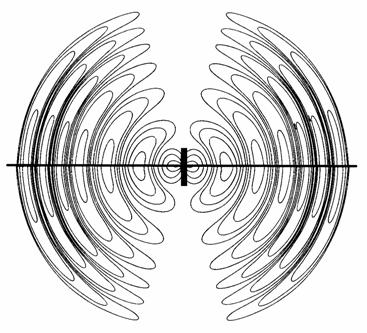
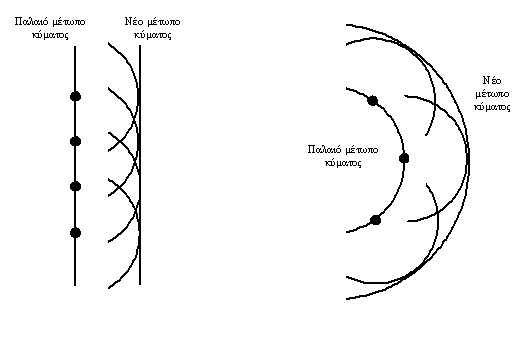

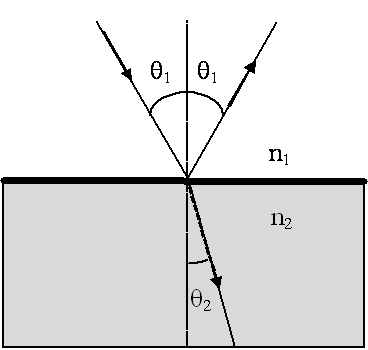
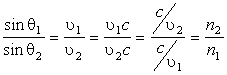 = σταθερά
= σταθερά