
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ
ΙΔΡΥΜΑ ΣΕΡΡΩΝ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ
Φυσική I
Δημήτριος Δ. Χασάπης
Καθηγητής
Τομέας Τηλεπικοινωνιών και Δικτύων
Σέρρες 2008

ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ
ΙΔΡΥΜΑ ΣΕΡΡΩΝ
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ
ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ
Φυσική I
Δημήτριος Δ. Χασάπης
Καθηγητής
Τομέας Τηλεπικοινωνιών και Δικτύων
Σέρρες 2008
ΣΤΑΤΙΚΟΣ ΗΛΕΚΤΡΙΣΜΟΣ
Στα επόμενα κεφάλαια
θα ασχοληθούμε με τον στατικό ηλεκτρισμό, την μελέτη δηλαδή της
συμπεριφοράς ακίνητων ηλεκτρικών φορτίων.
Πειραματικά
αποδείχθηκαν οι ακόλουθες θεμελιώδεις ιδιότητες του ηλεκτρικού φορτίου:
1.
το ηλεκτρικό φορτίο εμφανίζεται με δύο μορφές, οι οποίες χαρακτηρίζονται σαν θετική και αρνητική.
2.
το συνολικό φορτίο
ενός κλειστού κυκλώματος
διατηρείται σταθερό.
3.
το ηλεκτρικό φορτίο είναι κβαντισμένο, υπάρχει δηλαδή
σε τυποποιημένα, πακετοποιημένα και όχι σε τυχαία, δηλαδή συνεχή ποσά.
«Πείραμα του Millikan»: όλα τα μετρούμενα
στην φύση ηλεκτρικά φορτία είναι ακέραια πολλαπλάσια μιας στοιχειώδους ποσότητας
φορτίου:
παρατηρούμενα στη φύση φορτία: ![]() [1.1]
[1.1]
όπου n = ακέραιος
αριθμός, -¥ < n < ¥
Στοιχειώδες ηλεκτρικό φορτίο: ![]() .
.
Aλληλεπίδραση των
δύο ακινήτων ηλεκτρικών σημειακών φορτίων:
|
|
|
|
Σχήμα 1.1: Εξήγηση της «γεωμετρίας» του νόμου του Coulomb. |
|
Νόμος του Coulomb: ![]()
![]() [1.2] Video1
[1.2] Video1
![]() , ε
= διηλεκτρική σταθερή του μέσου εντός του οποίου βρίσκονται τα φορτία q1 και q2.
, ε
= διηλεκτρική σταθερή του μέσου εντός του οποίου βρίσκονται τα φορτία q1 και q2.
Η διηλεκτρική σταθερή του κενού
συμβολίζεται με ε0 και έχει την τιμή:
![]() .
.
Παρατηρήσεις: Στην εξίσωση [1.2] α) Τα φορτία q1 και q2 λαμβάνονται μαζί με το πρόσημό τους.
β)
Το μοναδιαίο διάνυσμα ![]() έχει φορά προς το
φορτίο, το οποίο δέχεται την επίδραση της δύναμης
έχει φορά προς το
φορτίο, το οποίο δέχεται την επίδραση της δύναμης ![]() .
.
γ) Από το α) και
β) προκύπτει, ότι στην περίπτωση ομωνύμων φορτίων τα διανύσματα ![]() και
και ![]() είναι ομόρροπα, ενώ
στην αντίθετη αντίρροπα:
είναι ομόρροπα, ενώ
στην αντίθετη αντίρροπα:
δ) Πειραματικά
αποδεικνύεται, ότι
Η δύναμη Coulomb μεταξύ δύο σημειακών
φορτίων είναι ανεξάρτητη από την παρουσία άλλων φορτίων.
H ολική δύναμη Coulomb, την οποία
δέχεται ένα σημειακό φορτίο από άλλα σημειακά φορτία, υπολογίζεται ως εξής: (Αρχή
της γραμμικής υπερθέσεως):
α) Σύστημα Ν σημειακών φορτίων qi:
![]() [1.2α]
[1.2α]
όπου ri = απόσταση μεταξύ q και qi
![]() = μοναδιαίο διάνυσμα στην κατεύθυνση qi ® q
= μοναδιαίο διάνυσμα στην κατεύθυνση qi ® q
β)
Συνεχής κατανομή φορτίου: ![]() [1.2β]
[1.2β]
|
|
όπου ρ =:dq/dV πυκνότητα
φορτίου
(αν το φορτίο
κατανέμεται επιφανειακά (ή γραμμικά), αντικαθιστούμε την πυκνότητα φορτίου με
την επιφανειακή πυκνότητα φορτίου σ = dq/dS (ή γραμμική πυκνότητα φορτίου λ = dq/dl ), και το στοιχείο
όγκου dV με το
στοιχείο επιφάνειας dS (ή μήκους dl))
1.2 Η ένταση του ηλεκτρικού πεδίου
Ένταση του
ηλεκτροστατικού πεδίου: καλείται το διανυσματικό μέγεθος ![]() , το οποίο έχει την διεύθυνση και φορά της δύναμης
, το οποίο έχει την διεύθυνση και φορά της δύναμης ![]() , η οποία ασκείται σε (συμβατικά!) θετικό
μοναδιαίο φορτίο +q, το οποίο βρίσκεται στο συγκεκριμένο σημείο:
, η οποία ασκείται σε (συμβατικά!) θετικό
μοναδιαίο φορτίο +q, το οποίο βρίσκεται στο συγκεκριμένο σημείο:
![]() [1.3]
[1.3]
όπου: ![]() είναι η συνολική
δύναμη Coulomb, η οποία
ασκείται στο φορτίου +q, όταν αυτό βρίσκεται στο συγκεκριμένο σημείο του πεδίου.
είναι η συνολική
δύναμη Coulomb, η οποία
ασκείται στο φορτίου +q, όταν αυτό βρίσκεται στο συγκεκριμένο σημείο του πεδίου.
Αν γνωρίζουμε
την ένταση ![]() την δύναμη
την δύναμη ![]() :
:
![]() [1.4]
[1.4]
Οι δυναμικές
γραμμές «αισθητοποιούν» το πεδίο, μια και σχεδιάζονται έτσι
ώστε
α) Η διεύθυνση της εφαπτομένης σε κάποιο σημείο μιας
δυναμικής γραμμής συμπίπτει με εκείνη της έντασης πεδίου στο σημείο αυτό.
β) Η φορά των ηλεκτρικών δυναμικών γραμμών συμπίπτει με
την φορά της έντασης. Επομένως οι ηλεκτρικές δυναμικές γραμμές πηγάζουν από
θετικά και καταλήγουν σε αρνητικά φορτία
γ) Ο αριθμός των δυναμικών γραμμών, οι οποίες
διέρχονται από την μοναδιαία επιφάνεια, κάθετης στην ένταση ![]() , του πεδίου στο κέντρο της μοναδιαίας επιφάνειας,
είναι ανάλογος προς το μέτρο της έντασης στο σημείο αυτό.
, του πεδίου στο κέντρο της μοναδιαίας επιφάνειας,
είναι ανάλογος προς το μέτρο της έντασης στο σημείο αυτό.
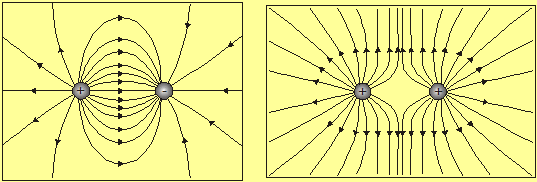
Σχήμα 1.2: Δυναμικές γραμμές συστήματος δύο ετερώνυμων
και ομώνυμων φορτίων.

Σχήμα 1.3: Δυναμικές γραμμές
|
Σχήμα 1.5: Υπολογισμός της ροής μέσω τυχαίας μακροσκοπικής
επιφάνειας |
|
Σχήμα 1.4: Περιγραφή του μεγέθους και του προσανατολισμού
στοιχειώδους επιφάνειας με την βοήθεια διανύσματος |
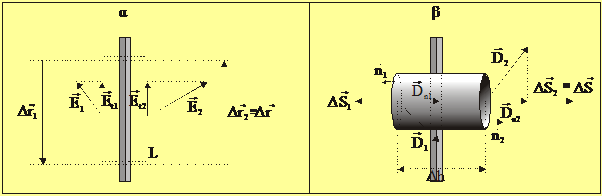
1.4 Ροή του ηλεκτρικού πεδίου
Ηλεκτρική ροή dΦ μέσω μιας στοιχειώδους
επιφάνειας dS, η οποία βρίσκεται εντός ηλεκτρικού πεδίου εντάσεως ![]() , καλείται το γινόμενο
, καλείται το γινόμενο
![]() [1.5]
[1.5]
η ( στοιχειώδης) ηλεκτρική ροή dΦ =Ε dS cosθ ισούται με τον αριθμό
των δυναμικών γραμμών, οι οποίες περνούν («κάθετα») από την (στοιχειώδη)
επιφάνεια dS ( δηλαδή μέσω της κάθετης προς την ![]() προβολής της).
προβολής της).
Όταν η
επιφάνεια είναι μακροσκοπική
παίρνουμε:
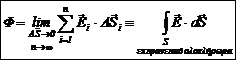 [1.5α]
[1.5α]
Αν η επιφάνεια
είναι κλειστή, η σχέση [ 1.5α ] γράφεται:
![]() [1.5β]
[1.5β]
1.5 Ο νόμος του Gauss
![]() (Νόμος του
Gauss) [1.6]
(Νόμος του
Gauss) [1.6]
q = ολικό
φορτίο εντός της κλειστής επιφάνειας
Σύμφωνα με τον νόμο του Gauss η ηλεκτρική ροή μέσω
οποιασδήποτε κλειστής επιφάνειας ισούται με το πηλίκο του ολικού φορτΙου (= άθροισμα όλων των επιμέρους φορτίων), το οποίο βρίσκεται εντός της
επιφάνειας, προς την διηλεκτρική σταθερή του κενού.
εφαρμογές
1η ) Πεδίο σφαιρικής κατανομής φορτίου:
|
Σχήμα 1.8: Σφαιρική κατανομή φορτίου. |
Σύμφωνα με τον
νόμο του Gauss η ροή μέσω μιας
τέτοιας επιφάνειας(Gauss, όπως λέγεται) είναι:
![]()
![]() [1.7]
[1.7]
(Ένταση του πεδίου σφαιρικής κατανομής
φορτίου σε απόσταση r από το κέντρο της. Στην [1.7] q είναι το
φορτίο, το οποίο περικλείει σφαιρική επιφάνεια ακτίνας r και κέντρου ίδιου με εκείνο της σφαιρικής κατανομής).
|
Σχήμα 1.10: Υπολογισμός του
πεδίου λεπτού ευθυγράμμου σύρματος με τον νόμο του Gauss. |
2η )
Πεδίο λεπτού, ευθυγράμμου σύρματος: Ένα φορτισμένο, λεπτό σύρμα
αποτελεί ένα καλό παράδειγμα για την υλοποίηση της γραμμικής κατανομής
φορτίου. Με εξαίρεση την περιοχή των άκρων του, τα οποία στην περίπτωση
ενός μακριού σύρματος παίζουν ασήμαντο ρόλο, το ηλεκτρικό πεδίο θα κατευθύνεται
λόγω συμμετρίας ακτινικά.
Σύμφωνα λοιπόν
με τον νόμο του Gauss θα έχουμε: ![]()
![]() [1.8]
[1.8]
![]()
|
Σχήμα 1.11: Υπολογισμός του πεδίου λεπτής, επίπεδης
πλάκας απείρων διαστάσεων. |
3η) Πεδίο λεπτής, επίπεδης, φορτισμένης πλάκας απείρων διαστάσεων:
Στην προκειμένη
περίπτωση η κατανομή φορτίου είναι, λόγω του αμελητέου πάχους, επιφανειακή,
οπότε χαρακτηρίζεται από την επιφανειακή πυκνότητα φορτίου σ = dq/dS.
Επομένως ο νόμος
του Gauss μας δίνει
![]()
![]() [1.9]
[1.9]
Στις
περιπτώσεις, κατά τις οποίες είναι αδύνατο να ευρεθεί μια κατάλληλη επιφάνεια Gauss, η ένταση του
ηλεκτροστατικού πεδίου υπολογίζεται με την βοήθεια του νόμου του Coulomb, κατά τον
ακόλουθο τρόπο:
α) Περίπτωση δύο ή περισσοτέρων σημειακών
φορτίων:
![]() [1.10]
[1.10]
όπου ri = απόσταση μεταξύ
qi και σημείου,
στο οποίο υπολογίζουμε το πεδίο
![]() = μοναδιαίο
διάνυσμα στην κατεύθυνση qi ® σημείο
υπολογισμού
= μοναδιαίο
διάνυσμα στην κατεύθυνση qi ® σημείο
υπολογισμού
β) Περίπτωση συνεχούς κατανομής φορτίου:
|
Σχήμα 1.12: Υπολογισμός
πεδίου συνεχούς κατανομής φορτίου. |
![]() [1.11]
[1.11]
(αν το φορτίο κατανέμεται επιφανειακά (ή γραμμικά), αντικαθιστούμε την
πυκνότητα φορτίου ρ=dq/dV με την επιφανειακή πυκνότητα φορτίου σ=dq/dS (ή γραμμική πυκνότητα φορτίου λ=dq/dl), και το στοιχείο όγκου dV με το στοιχείο επιφανείας dS (ή μήκους dl))
1.6 Δυναμικό του ηλεκτροστατικού πεδίου
Δυνάμεις, των
οποίων το έργο δεν εξαρτάται από την συγκεκριμένη διαδρομή, αλλά απλώς, από το
σημείο εκκίνησης (Α) και το σημείο άφιξης (Β), καλούνται συντηρητικές.
Κατ’ επέκταση
καλούνται συντηρητικά και τα αντίστοιχα πεδία δυνάμεων.
Το
ηλεκτροστατικό και το βαρυτικό πεδίο είναι, συντηρητικά.
Συντηρητικά
πεδία μπορούν να χαρακτηρισθούν πλήρως με την βοήθεια μιας μονόμετρης
συναρτήσεως, του δυναμικού U(![]() ):
):
Δυναμικό UΣ ενός
ηλεκτροστατικού πεδίου σε σημείο Σ καλείται το πηλίκο του έργου ![]() , το οποίο απαιτείται για να μετακινηθεί (συμβατικά θετικό) ηλεκτρικό φορτίο q από το ¥ μέχρι το σημείο Σ, προς το φορτίο q:
, το οποίο απαιτείται για να μετακινηθεί (συμβατικά θετικό) ηλεκτρικό φορτίο q από το ¥ μέχρι το σημείο Σ, προς το φορτίο q:
![]() [1.12]
[1.12]
Ή δυναμικό UΣ ενός ηλεκτροστατικού πεδίου σε ένα
σημείο Σ καλείται η δυναμική ενέργεια, την οποία κατέχει η θετική μονάδα
φορτίου στο σημείο Σ και (συμβατικά) σε σχέση με το ¥, δηλαδή το έργο το οποίο παράγεται
υπό του πεδίου κατά την μετακίνηση της θετικής μονάδας φορτίου από το
σημείο Σ ως το ¥:
![]() [1.13]
[1.13]
Μεταξύ του
δυναμικού και της έντασης του ηλεκτρικού πεδίου ισχύει η σχέση:
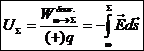 [1.14]
[1.14]
1.6.1 Πρακτικός υπολογισμός του δυναμικού
α) δυναμικό οφειλόμενο σε ένα σημειακό φορτίο Q σε απόσταση r από το φορτίο:
Σύμφωνα τώρα με
την εξίσωση [ 1.14 ] έχουμε:
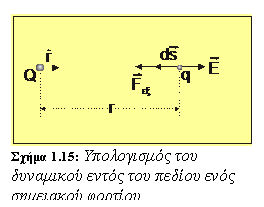
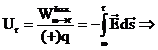
![]() [1.15]
Video2, Video3, Video4
[1.15]
Video2, Video3, Video4
β) δυναμικό
οφειλόμενο σε ομάδα σημειακών φορτίων Qi:
![]() [1.16]
[1.16]
όπου N = συνολικός
αριθμός των φορτίων Qi
ri = απόσταση του εξεταζόμενου φορτίου από το
φορτίο Qi
γ) δυναμικό οφειλόμενου σε συνεχή κατανομή φορτίου:
|
Σχήμα 1.16: Υπολογισμός του δυναμικού συνεχούς
κατανομής φορτίου. |
![]() [1.17]
[1.17]
(αν το φορτίο κατανέμεται επιφανειακά (ή γραμμικά), αντικαθιστούμε την
πυκνότητα φορτίου ρ=dq/dV με την επιφανειακή πυκνότητα φορτίου σ=dq/dS (ή γραμμική πυκνότητα φορτίου λ = dq/dl), και το στοιχείο όγκου dV με το στοιχείο
επιφανείας dS (ή μήκους dl)).
1.7 Υπολογισμός της έντασης του ηλεκτροστατικού πεδίου από το δυναμικό του
Από μαθηματική
άποψη το δυναμικό είναι απλώς ένα μονόμετρο (αριθμητικό) μέγεθος, του οποίου η
τιμή μεταβάλλεται σε συνάρτηση από τον τόπο: U = U(x,y,z).
Για το δυναμικό,
και γενικότερα για κάθε άλλο μονόμετρο πεδίο, μπορούμε να ορίσουμε ένα
διανυσματικό πεδίο την λεγόμενη βαθμίδα του ![]() , ως εξής:
, ως εξής:
![]() [1.18]
[1.18]
όπου ![]() = μοναδιαία διανύσματα
κατά μήκος των αξόνων χ, y και z αντίστοιχα.
= μοναδιαία διανύσματα
κατά μήκος των αξόνων χ, y και z αντίστοιχα.
![]() :Διανυσματικός
διαφορικός τελεστής Nabla
:Διανυσματικός
διαφορικός τελεστής Nabla
Η φυσική τώρα
υπόσταση της βαθμίδας του δυναμικού είναι η ακόλουθη:
η βαθμίδα του δυναμικού είναι ένα
διάνυσμα, το οποίο κατευθύνεται προς την περιοχή μέγιστης (ανά μονάδα μήκους)
αύξησης του δυναμικού, ίσης προς την απόλυτη τιμή της βαθμίδας.
Αποδεικνύεται
ότι: ![]() [1.19]
[1.19]
Σύμφωνα λοιπόν
με την σχέση [1.19]
η ένταση ![]() του ηλεκτροστατικού
πεδίου σε κάποιο σημείο του χώρου είναι ένα διάνυσμα, με φορά την κατεύθυνση
μέγιστης (ανά μονάδα μήκους) ελάττωσης του ηλεκτροστατικού δυναμικού U, ίσης με την απόλυτη τιμή της έντασης
του ηλεκτροστατικού
πεδίου σε κάποιο σημείο του χώρου είναι ένα διάνυσμα, με φορά την κατεύθυνση
μέγιστης (ανά μονάδα μήκους) ελάττωσης του ηλεκτροστατικού δυναμικού U, ίσης με την απόλυτη τιμή της έντασης ![]() .
.
Κανόνες
υπολογισμού της βαθμίδας
α, β = σταθερές, φ, ψ = μονόμετρα πεδία (συνεχόμενα
παραγωγίσιμα)
grad α= 0 grad (αφ + βψ ) = α grad φ + β grad ψ grad (φ ψ ) = φ grad ψ + ψ gradφ
grad (φ(ψ)) = (dφ / dψ ) grad ψ ![]()
όπου U(r) = κεντρικό
πεδίο: η τιμή του εξαρτάται μόνο από την απόσταση r από κάποιο συγκεκριμένο σημείο, το κέντρο του).
![]() = μοναδιαίο
διάνυσμα με κατεύθυνση από το κέντρο του πεδίου προς το σημείο που εξετάζουμε.
= μοναδιαίο
διάνυσμα με κατεύθυνση από το κέντρο του πεδίου προς το σημείο που εξετάζουμε.
1.8 Διαφορά δυναμικού ( ή τάση )
Διαφορά δυναμικού (ή τάση) μεταξύ
δύο σημείων καλείται η διαφορά των δυναμικών των δύο αυτών
σημείων:
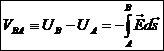 [1.20]
[1.20]
Ισοδυναμικές καλούνται οι επιφάνειες, των
οποίων όλα τα σημεία έχουν το ίδιο δυναμικό.
Στην περίπτωση ενός σημειακού φορτίου
οι ισοδυναμικές επιφάνειες είναι σφαιρικές με κέντρο το σημειακό φορτίο.
Η μετακίνηση
ενός σημειακού φορτίου επάνω σε οποιαδήποτε ισοδυναμική επιφάνεια ούτε παράγει
ούτε απαιτεί έργο και μάλιστα εξ ορισμού. Άρα η ένταση ![]() του πεδίου είναι κάθετη σε όλα τα σημεία μιας
ισοδυναμικής επιφάνειας. Επομένως οι δυναμικές γραμμές διαπερνούν κάθετα τις
ισοδυναμικές επιφάνειες.
του πεδίου είναι κάθετη σε όλα τα σημεία μιας
ισοδυναμικής επιφάνειας. Επομένως οι δυναμικές γραμμές διαπερνούν κάθετα τις
ισοδυναμικές επιφάνειες.
1.10 Αγωγοί μέσα σε ηλεκτροστατικό πεδίο
Το ηλεκτρικό πεδίο στο εσωτερικό
ενός αγωγού, ο οποίος βρίσκεται σε κατάσταση ηλεκτροστατικής ισορροπίας, είναι
μηδέν.
 Επομένως
Επομένως
ü
Όλα τα σημεία ενός αγωγού σε κατάσταση ηλεκτροστατικής ισορροπίας έχουν
το ίδιο δυναμικό.
ü
Η επιφάνεια ενός αγωγού σε κατάσταση
ηλεκτροστατικής ισορροπίας είναι ισοδυναμική επιφάνεια.
ü
Η ένταση του πεδίου στα σημεία της επιφάνειας αγωγού ευρισκόμενου σε
κατάσταση ηλεκτροστατικής ισορροπίας είναι κάθετη προς την επιφάνεια του
αγωγού.
Στον μηδενισμό
του πεδίου στο εσωτερικό ενός αγωγού στηρίζεται η ηλεκτροστατική θωράκιση: ένας χώρος θωρακίζεται έναντι
ηλεκτροστατικών πεδίων αν το περιβάλουμε με μεταλλικό περίβλημα. Σε πολλές
μάλιστα περιπτώσεις αρκεί ένα αρκετά πυκνό μεταλλικό δίκτυο, το λεγόμενο κλουβί του Faraday.
|
Σχήμα 1.19: Πλήρη εκφόρτιση αγωγού μέσω δοχείου Faraday. |
Εφαρμογές της ηλεκτροστατικής θωράκισης: Προστασία
επιστημονικών οργάνων και διαφόρων ηλεκτρονικών συσκευών (κυρίως στον τομέα
των τηλεπικοινωνιών) από ανεπιθύμητα ηλεκτροστατικά πεδία, δυνατότητα εργασίας
πλησίον εγκαταστάσεων υψηλής τάσεως, επιβάτες αυτοκινήτων και αεροπλάνων δεν
κινδυνεύουν από κεραυνούς.
ü
Στην κατάσταση ηλεκτροστατικής ισορροπίας
όλο το πλεονάζον φορτίο ενός φορτισμένου
(και μονωμένου) αγωγού κατανέμεται στην
εξωτερική του επιφάνεια.
Εφαρμογή του παραπάνω
φαινομένου αποτελεί το λεγόμενο δοχείο του Faraday (βλ. σχήμα 1.19),
το οποίο μπορεί να χρησιμοποιηθεί για την πλήρη αποφόρτιση ενός φορτισμένου
αγωγού.
1.10.1Ένταση του πεδίου επί της ( εξωτερικής) επιφάνειας φορτισμένου αγωγού
|
Σχήμα 1.20: Υπολογισμός της έντασης του πεδίου πλησίον
της επιφανείας φορτισμένου αγωγού. |
Έστω ότι ένας αγωγός έχει φορτίο q και βρίσκεται
σε κατάσταση ηλεκτροστατικής ισορροπίας. Αν εφαρμόσουμε τον νόμο του Gauss για μια
στοιχειώδη κλειστή επιφάνεια Gauss (τυχαίου σχήματος), η οποία περιέχει το στοιχειώδες
τμήμα dS της επιφάνειας
του αγωγού ( βλ. σχ. 1.20), παίρνουμε:
![]() [1.21]
[1.21]
Όπως
αποδεικνύεται πειραματικά
η ένταση του πεδίου στα σημεία (και πλησίον) της επιφάνειας φορτισμένου
αγωγού, ευρισκόμενου σε κατάσταση ηλεκτροστατικής ισορροπίας, είναι αντιστρόφως
ανάλογη προς την ακτίνα καμπυλότητας της γεωμετρικής μορφής της επιφάνειάς του:
στις αιχμές (μικρή ακτίνα καμπυλότητας) μεγάλη, στα σημεία μικρής καμπυλότητας
μικρή.
Εφαρμογές: 1η
) Κατά τον σχεδιασμό εγκαταστάσεων υψηλής τάσης αποφεύγονται τα αιχμηρά
τμήματα προς αποφυγή ηλεκτρικών εκκενώσεων σαν συνέπεια ισχυρών πεδίων.
2η ) Με την βοήθεια των αλεξικέραυνων πετυχαίνουμε, μέσω του
ισχυρού πεδίου στην κορυφή τους, την λεγόμενη «σιωπηλή» εκκένωση. Με τον τρόπο
αυτό πραγματοποιείται ανταλλαγή φορτίου με την ατμόσφαιρα, χωρίς τις
καταστροφικές συνέπειες του κεραυνού.
3η ) Η εξαγωγή ηλεκτρονίων από ένα μέταλλο με την βοήθεια ηλεκτρικού πεδίου («εκπομπή πεδίου»)
απαιτεί εντάσεις της τάξεως 109 V/m. Με την βοήθεια μεταλλικών ακίδων
ακτίνας 1μm πετυχαίνουμε
τέτοιες εντάσεις με τάσεις μερικών μόνο εκατοντάδων Volts. (κάθοδοι πεδίου).
Το ηλεκτρικό
πεδίο διαπερνά τα μονωτικά υλικά. Αυτός είναι και ο λόγος για τον οποίο οι
(εντός ηλεκτρικών πεδίων ευρισκόμενοι) μονωτές χαρακτηρίζονται και ως διηλεκτρικά.
Πυκνωτής καλείται κάθε ζεύγος γειτονικών,
μονωμένων αγωγών τυχαίου σχήματος και γεωμετρίας.
Οι δύο
αγωγοί ονομάζονται οπλισμοί.
Ανάλογα με το σχήμα τους διακρίνουμε σφαιρικούς, κυλινδρικούς και
επίπεδους πυκνωτές.
Σαν μονωτικό
μεταξύ των δύο οπλισμών παρεμβάλλεται κενό ή κάποιο άλλο μονωτικό υλικό.
Εφαρμογές: Αποθήκευση ηλεκτρικής ενέργειας, με την μορφή
ηλεκτρικού πεδίου περιορισμένου ουσιαστικά στον μεταξύ των οπλισμών
ευρισκόμενο χώρο.
Μορφές πυκνωτών: α) Πυκνωτές
κενού: Οι οπλισμοί είναι κλεισμένοι μέσα σε δοχεία υψηλού κενού.
Χρησιμοποιούνται όπου υπάρχουν πολύ υψηλά και γρήγορα μεταβαλλόμενα δυναμικά.
β) Φυλλωτοί πυκνωτές: Οι οπλισμοί τους
αποτελούνται από λεπτά μεταλλικά ή συνθετικά φύλλα και τυλίγονται έτσι ώστε να
έχουν μικρό όγκο (βλ. σχ.2a ).
γ)
Ηλεκτρολυτικοί πυκνωτές: Ο ένας εκ των δύο οπλισμών είναι ένας
ηλεκτρολύτης, εντός του οποίου είναι βυθισμένος ο δεύτερος μεταλλικός οπλισμός,
ο οποίος περιβάλλεται από λεπτό στρώμα οξειδίου, το διηλεκτρικό (βλ. σχ.2b ) Έχουν σχετικά
μεγάλη χωρητικότητα, το οξείδιο όμως αντέχει μόνο σε χαμηλές τάσεις
λειτουργίας.
δ) Μεταβλητοί πυκνωτές: Επιτρέπουν την συνεχόμενη μεταβολή της
χωρητικότητας τους μέσω μεταβολής της δρώσας επιφάνειας των οπλισμών τους
(βλ.σχ.2c).
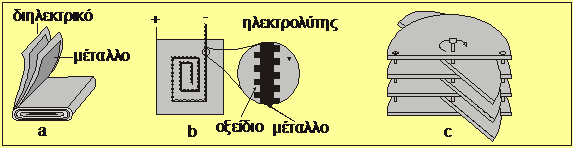
Σχήμα 2: Διάφορες μορφές πυκνωτών: a: φυλλωτός, b:
ηλεκτρολυτικός, c: μεταβλητός
|
συμβολισμός πυκνωτή: |
χωρητικότητα πυκνωτή:
![]() [2.2α]
[2.2α]
όπου: V =
διαφορά δυναμικού μεταξύ των οπλισμών
Q = φορτίο, ενός εκ
των δύο οπλισμών
Η χωρητικότητα ενός πυκνωτή εξαρτάται, μόνο από την μορφή
του (γεωμετρική κατανομή του φορτίου του), τις διαστάσεις του και το
διηλεκτρικό μεταξύ των οπλισμών του.
Μονάδες χωρητικότητας :
[C] = ![]()
Στην πράξη
χρησιμοποιούνται τα υποπολλαπλάσια μF (º10-
2.3 Υπολογισμός της χωρητικότητας ορισμένων μορφών πυκνωτών
α) Επίπεδος πυκνωτής: Το πεδίο είναι περιορισμένο
κατά κύριο λόγο μεταξύ των οπλισμών και είναι ουσιαστικά ομογενές ( βλ. σχ.
2.1) με εξαίρεση τα άκρα, τα οποία όμως παίζουν τόσο μικρότερο λόγο όσο
ελαττώνεται η απόσταση των οπλισμών.
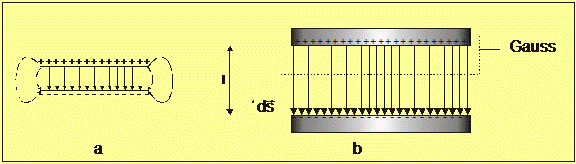
Σχήμα 2.1.
Η χωρητικότητα
δίνεται από την σχέση: ![]() { 1
}
{ 1
}
Ο υπολογισμός
του φορτίου Q του ενός
οπλισμού μπορεί να γίνει με την βοήθεια του νόμου του Gauss:
![]() { 2 } :
{ 2 } :
Η διαφορά
δυναμικού V μεταξύ των οπλισμών
υπολογίζεται από την γενική σχέση:
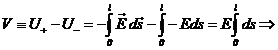
![]() [2.3]
[2.3]
Αντικαθιστώντας στην {1} παίρνουμε:
|
|
:Χωρητικότητα
επίπεδου πυκνωτή με κενό σαν διηλεκτρικό |
[2.4] |
όπου S = επιφάνεια οπλισμού
l = απόσταση οπλισμών
|
Σχήμα 2.2 |
β) Σφαιρικός πυκνωτής: Στον σφαιρικό
πυκνωτή οι οπλισμοί είναι ομόκεντρες σφαίρες ακτίναςR και r (<R) αντίστοιχα (βλ. σχ. 2.2).
Οι οπλισμοί του
αποτελούν χαρακτηριστικό παράδειγμα σφαιρικής
κατανομής φορτίου: ![]() {1}
{1}
όπου r η απόσταση από το κέντρο των οπλισμών
και Q το φορτίο του
μικρού οπλισμού.
Η τάση V μεταξύ των
οπλισμών θα είναι:
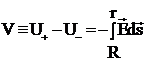 Þ
Þ ![]() { 2 }
{ 2 }
Η χωρητικότητα C του πυκνωτή θα
είναι:
|
: χωρητικότητα σφαιρικού
πυκνωτή οπλισμών ακτίνων R>r (διηλ. = κενό) |
![]() Þ
Þ ![]() [2.5]
[2.5]
γ) Κυλινδρικός πυκνωτής: Οι οπλισμοί ενός
κυλινδρικού πυκνωτή είναι δύο ομοαξονικοί κύλινδροι ακτίνας R και r ( < R) αντίστοιχα (
βλ. σχ. 2.3).
|
Σχήμα 2.3: Κάθετη τομή κυλινδρικού πυκνωτή |
Με την
προϋπόθεση λοιπόν ότι l >> R ο νόμος του Gauss μας δίνει:
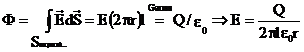 {1}
{1}
Η τάση V μεταξύ των
οπλισμών υπολογίζεται ως εξής:
![]() Þ
Þ ![]() {2}
{2}
Η χωρητικότητα
τέλος του κυλινδρικού πυκνωτή θα είναι:
|
|
Χωρητικότητα κυλινδρικού
πυκνωτή ακτίνων R και r και μήκους l (l>>R>r, διηλ. = κενό) |
[2.6] |
α) Πυκνωτές σε
παράλληλη σύνδεση:
|
|
Στην παράλληλη σύνδεση η τάση μεταξύ των οπλισμών είναι για όλους τους
πυκνωτές εξ ορισμού η ίδια: ![]() {1}
{1}
Επομένως το ολικό φορτίο θα μοιράζεται στους επιμέρους πυκνωτές ανάλογα με την
χωρητικότητα τους. Άρα το ολικό
φορτίο ισούται με το άθροισμα των φορτίων
(π.χ. των θετικά φορτισμένων οπλισμών) των μεμονωμένων πυκνωτών: ![]() {2}
{2}
Η ισοδύναμη ή
ολική χωρητικότητα C ορίζεται ως η χωρητικότητα ενός μόνου πυκνωτή, ο
οποίος έχει φορτίο ίσο με το ολικό φορτίο της συστοιχίας, όταν στα άκρα του
εφαρμόζεται η ίδια τάση με εκείνη της συστοιχίας:
![]()
Στην γενική
περίπτωση k παράλληλα
συνδεμένων πυκνωτών έχουμε επομένως:
|
|
Ολική χωρητικότητα παράλληλης συστοιχίας k πυκνωτών [2.7] |
β) Πυκνωτές σε σύνδεση κατά σειρά:
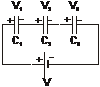 στη σύνδεση κατά σειρά το φορτίο όλων των πυκνωτών είναι το ίδιο και ίσο με
το ολικό φορτίο της συστοιχίας:
στη σύνδεση κατά σειρά το φορτίο όλων των πυκνωτών είναι το ίδιο και ίσο με
το ολικό φορτίο της συστοιχίας:
q1= q2= q3= qολºQ {3}
Επομένως η ολική τάση θα μοιράζεται στους επιμέρους πυκνωτές ανάλογα με την
χωρητικότητα τους. Άρα η
ολική τάση VºVολ ισούται με το άθροισμα των τάσεων μεμονωμένων πυκνωτών:
VºVολ=V1+V2+V3 {4}
Η ολική
χωρητικότητα C θα είναι:
![]()
![]() Στην γενική
περίπτωση k σε σειρά συνδεομένων πυκνωτών έχουμε επομένως:
Στην γενική
περίπτωση k σε σειρά συνδεομένων πυκνωτών έχουμε επομένως:
|
|
2.5 Ενέργεια μιας κατανομής φορτίου
![]()
![]() [2.9]
[2.9]
Στην περίπτωση
της φόρτισης ενός πυκνωτή θα πρέπει να αντικαταστήσουμε το δυναμικό U με την τάση V μεταξύ των
οπλισμών:
Ενέργεια φορτισμένου πυκνωτή: ![]() [2.
9α]
[2.
9α]
2.5.1 Το ηλεκτρικό πεδίο ως φορέας της ηλεκτρικής ενέργειας
Η ενέργεια ενός
επίπεδου πυκνωτή χωρητικότητας C, θα είναι σύμφωνα
με την σχέση [2.9α]:
![]()
![]()
όπου v = όγκος
του χώρου μεταξύ των οπλισμών, δηλαδή του χώρου μέσα στον οποίο
εκτείνεται το πεδίο.
Η σχέση αυτή
διατηρεί την ισχύ της ακόμη και στην γενική περίπτωση ενός μη ομογενούς
πεδίου, αρκεί να χρησιμοποιηθεί η πυκνότητα
ενέργειας:
Πυκνότητα ενέργειας του ηλεκτρικού πεδίου: ![]() [2.10]
[2.10]
Στην γενική αυτή
περίπτωση η πυκνότητα ενέργειας μεταβάλλεται από σημείο σε σημείο.
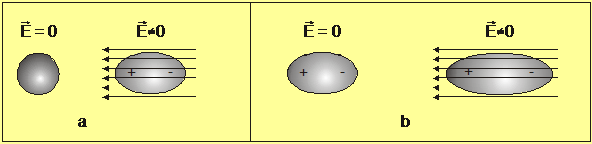
2.6 Δίπολα
Ηλεκτρικό δίπολο καλείται κάθε
ζεύγος δύο ίσων και αντίθετων σημειακών φορτίων ευρισκομένων πολύ κοντά
το ένα στο άλλο.
Οι ηλεκτρικές
ιδιότητες ενός δίπολου μπορούν να περιγραφούν πολύ κομψά από μαθηματική άποψη
με την βοήθεια ενός διανύσματος, το οποίο καλείται
|
|
Διπολική
ροή: |
Το δίπολο μέσα σε ομογενές ηλεκτρικό πεδίο: Όταν το δίπολο
βρεθεί μέσα σε ομογενές ηλεκτρικό πεδίο
έντασης ![]() , δέχεται την επίδραση ζεύγους δυνάμεων
, δέχεται την επίδραση ζεύγους δυνάμεων ![]() και
και ![]() , το οποίο ασκεί επί του δίπολου μηχανική ροπή
, το οποίο ασκεί επί του δίπολου μηχανική ροπή
![]() [2.13]
[2.13]
![]() : μηχανική ροπή, εξασκούμενη επί διπόλου ηλεκτρικής
ροπής
: μηχανική ροπή, εξασκούμενη επί διπόλου ηλεκτρικής
ροπής ![]() εντός ομογενούς
ηλ. πεδίου έντασης
εντός ομογενούς
ηλ. πεδίου έντασης ![]() .
.
|
Σχήμα 2.4: Δίπολο εντός ομογενούς ηλ. πεδίου. |
Το μέτρο Μ
της μηχανικής ροπής είναι:
Μ =pΕsinθ [2.13α], ενώ η φορά της φαίνεται από το σχήμα 2.4.
Επομένως η μηχανική
ροπή μηδενίζεται, όταν η ηλεκτρική ροπή p (άρα και ο άξονας του διπόλου) γίνει παράλληλη προς την διεύθυνση του
πεδίου.
Τα μόρια εκείνα,
στα οποία δεν συμπίπτουν τα κέντρα κατανομής των θετικών και αρνητικών τους
φορτίων, έχουν (μόνιμη) διπολική ροπή και αποτελούν δείγματα φυσικών
διπόλων.
Υλικά, των
οποίων τα μόρια έχουν μόνιμη διπολική ροπή ονομάζονται πολικά (π.χ.
νερό/Η2Ο, υδροχλώριο /ΗCl, αμμωνία / ΝΗ3 ). Τα υπόλοιπα ονομάζονται
μη πολικά.
Το πηλίκο της
χωρητικότητας C ενός επίπεδου
πυκνωτή, όταν ολόκληρος ο χώρος μεταξύ των οπλισμών του είναι γεμάτος με
κάποιο διηλεκτρικό, προς την χωρητικότητα C0 του ίδιου
πυκνωτή στο κενό καλείται διηλεκτρικός αριθμός :
![]() [2.14]
[2.14]
Εφαρμογές: Διηλεκτρικά υψηλού διηλεκτρικού αριθμού επιτρέπουν
την κατασκευή πυκνωτών σχετικά μεγάλης χωρητικότητας και μικρών διαστάσεων.
Συνθετικά κεραμικά διηλεκτρικά, τα οποία περιέχουν οξείδιο του Βαρίου (BaO) και οξείδιο
του Τιτανίου (TiO), έχουν για
παράδειγμα διηλεκτρικούς αριθμούς της τάξεως 103 - 104.
Παρόμοια αύξηση της χωρητικότητας επιτυγχάνεται εξάλλου με την βοήθεια
λεπτότατων στρωμάτων διηλεκτρικού, όπως στην περίπτωση των ηλεκτρολυτικών
πυκνωτών. Η χρήση, τέλος, των διηλεκτρικών έχει επιπλέον και ένα άλλο
«μηχανικό» πλεονέκτημα: εμποδίζει τους οπλισμούς του πυκνωτή να έρθουν σε επαφή
αυξάνοντας έτσι την ανθεκτικότητα των πυκνωτών σε μηχανικές καταπονήσεις, όπως
π.χ. είναι οι κραδασμοί.
Η εξασθένιση λοιπόν του πεδίου παρουσία διηλεκτρικού οφείλεται στην εμφάνιση φορτίων στην
επιφάνεια του διηλεκτρικού (βλ. σχ. 2.5). Το φαινόμενο αυτό καλείται πόλωση
του διηλεκτρικού, όρος ο οποίος θα αποσαφηνιστεί στην συνέχεια.
Το φορτίο
πολώσεως δημιουργεί ένα νέο πεδίο έντασης Εp=Qp /(ε0 S) º σp / ε0
, όπου σp είναι η επιφανειακή πυκνότητα του
φορτίου πολώσεως.
Το πεδίο
πολώσεως ![]() είναι αντίθετο προς το πεδίο
είναι αντίθετο προς το πεδίο ![]() , το οποίο οφείλεται στο φορτίο Q0 του πυκνωτή.
Έτσι το συνολικό πεδίο
, το οποίο οφείλεται στο φορτίο Q0 του πυκνωτή.
Έτσι το συνολικό πεδίο ![]() είναι μειωμένο στο
εσωτερικό του διηλεκτρικού και μάλιστα κατά τον παράγοντα 1/εr:
είναι μειωμένο στο
εσωτερικό του διηλεκτρικού και μάλιστα κατά τον παράγοντα 1/εr:
Πεδίο εντός ομογενούς και ισότροπου διηλεκτρικού
ευρισκόμενου εντός του ομογενούς πεδίου επίπεδου πυκνωτή
|
|
|
(πεδίο στο εσωτερικό του ομογενούς και ισότροπου διηλεκτρικού επίπεδου
πυκνωτή) |
[2.15] |
Διηλεκτρική
πόλωση ![]() ενός διηλεκτρικού καλείται η
συνολική ηλεκτρική ροπή της μονάδας όγκου του διηλεκτρικού:
ενός διηλεκτρικού καλείται η
συνολική ηλεκτρική ροπή της μονάδας όγκου του διηλεκτρικού: ![]() , P = σp [2.16]
, P = σp [2.16]
Όπου σp : επιφανειακή
πυκνότητα του φορτίου (πολώσεως).
Αφού πάρουμε
υπόψη και την φορά των διανυσμάτων ![]() παίρνουμε:
παίρνουμε:
![]() [2.17]
[2.17]
όπου ![]() :διηλεκτρική επιδεκτικότητα [2.18]
:διηλεκτρική επιδεκτικότητα [2.18]
Παρατηρήσεις: 1η ) Η σχέση [2.17]
ισχύει για ομογενή και ισότροπα διηλεκτρικά ακόμη και στην περίπτωση που
το πεδίο ![]() είναι μη ομογενές.
είναι μη ομογενές.
2η ) Στην περίπτωση μη
ισότροπου διηλεκτρικού η διηλεκτρική πόλωση εξαρτάται από τον
προσανατολισμό του. Έτσι η διηλεκτρική επιδεκτικότητα χ δεν είναι πλέον
μονόμετρο μέγεθος αλλά τανυστής 2ου μεγέθους.
3η
) Υπάρχει μια κατηγορία υλικών, τα λεγόμενα σιδηροηλεκτρικά (σε αντιστοιχία με τα σιδηρομαγνητικά),
των οποίων η επιδεκτικότητα εξαρτάται τόσο από την ένταση του πεδίου όσο και
από την προϊστορία τους. Σε ορισμένες
περιπτώσεις η πόλωση μεταβάλλεται, εάν το υλικό θερμανθεί. Τέτοια υλικά
χαρακτηρίζονται συνήθως σαν πυροηλεκτρικά.
|
Σχήμα 2.6 |
α) Επιφανειακή πυκνότητα του φορτίου πολώσεως επί της επιφάνειας διηλεκτρικού,
το οποίο περιβάλλεται από κενό (σχ. 2.6): ![]() [2.18]
[2.18]
Το ολικό φορτίο πολώσεως επί της εξωτερικής επιφάνειας οποιουδήποτε
διηλεκτρικού, το οποίο περιβάλλεται, από κενό
θα είναι:
![]() [2.18α]
[2.18α]
β) Επιφανειακή πυκνότητα του φορτίου πολώσεως επί της διαχωριστικής
επιφάνειας δύο διαφορετικών διηλεκτρικών (σχ. 2.7):
![]() [2.19]
[2.19]
→ Η επιφανειακή
πυκνότητα του φορτίου πολώσεως επί μιας τυχαίας επιφάνειας στο εσωτερικό ενός ομογενούς και ισότροπου
διηλεκτρικού ισούται με μηδέν.
|
Σχήμα 2.7 |
|
Σχήμα 2.8 |
γ) φορτίο
πολώσεως εντός κλειστής επιφάνειας S στο εσωτερικό ενός διηλεκτρικού (βλ. σχ. 2.8)
![]() [2.20]
[2.20]
Ας θεωρήσουμε
τώρα μια τυχαία κλειστή επιφάνεια S, η οποία περικλείει διάφορους αγωγούς και
διηλεκτρικά ή τμήματα αυτών. Όσο πολύπλοκη και αν είναι η μορφή του
πεδίου, πάντα θα ισχύει ο νόμος του Gauss:
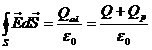 {1},
{1},
όπου Q = ολικό
«πραγματικό» φορτίο εντός της επιφάνειας
S.
Qp = ολικό φορτίο πολώσεως εντός της επιφάνειας S.
Αν στην σχέση
{1} αντικαταστήσουμε το φορτίο πολώσεως από την σχέση [2.20], θα
πάρουμε:
![]() :Γενική
διατύπωση του νόμου του Gauss [2.21]
:Γενική
διατύπωση του νόμου του Gauss [2.21]
όπου ![]() [2.22]
[2.22]
: Ηλεκτρική
διαταραχή ή μετατόπιση
ε
= : ![]() :διηλεκτρική
σταθερή [2.23]
:διηλεκτρική
σταθερή [2.23]
Η διηλεκτρική σταθερή στην περίπτωση ανισότροπων
διηλεκτρικών δεν είναι μονόμετρο μέγεθος αλλά τανυστής 2ου μεγέθους,
με αποτέλεσμα τα διανύσματα ![]() και
και ![]() να έχουν
διαφορετικές διευθύνσεις. Επιπλέον η διηλεκτρική σταθερή των σιδηροηλεκτρικών
υλικών εξαρτάται και από την ένταση
να έχουν
διαφορετικές διευθύνσεις. Επιπλέον η διηλεκτρική σταθερή των σιδηροηλεκτρικών
υλικών εξαρτάται και από την ένταση ![]() του ηλεκτρικού πεδίου.
του ηλεκτρικού πεδίου.
|
Σχήμα 2.9: |
δ) Συνολικό
πεδίο εντός ενός ομογενούς και ισότροπου ρευστού διηλεκτρικού απείρων ( ≈
πολύ μεγάλων ) διαστάσεων: Ας θεωρήσουμε
ένα δοχείο ( βλ. σχ. 2.9), το οποίο περιέχει κάποιο ηλεκτρικά ουδέτερο,
ομογενές και ισότροπο, υγρό διηλεκτρικό. Μέσα σ’ αυτό το υγρό βυθίζουμε ένα
φορτισμένο σφαιρίδιο, οπότε το πρώτο πολώνεται.
Το συνολικό
ηλεκτρικό πεδίο εντός του υγρού ισούται
με το άθροισμα των πεδίων, τα οποία δημιουργούνται από το πραγματικό φορτίο
του σφαιριδίου και τα φορτία
πολώσεως. Στην περίπτωση ενός
διηλεκτρικού, το οποίο εκτείνεται απεριόριστα προς όλες τις κατευθύνσεις
χρειάζεται να πάρουμε υπόψη την συμμετοχή μόνο εκείνων των φορτίων πολώσεως, τα
οποία περιβάλλουν το φορτισμένο σφαιρίδιο.
|
Σχήμα 2.10 |
![]()
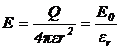 {1}
{1}
Το ηλεκτρικό πεδίο ενός συστήματος αγωγών τυχαίου σχήματος και γεωμετρίας, οι
οποίοι βρίσκονται εντός ενός απεριόριστου, ομογενούς και ισότροπου ρευστού διηλεκτρικού,
είναι μειωμένο σε σχέση με την τιμή του απουσία του διηλεκτρικού κατά τον
διηλεκτρικό αριθμό εr του διηλεκτρικού.
|
στην περίπτωση αγωγών (βλ. κεφ. 1.11 και 1.11.1) |
|
|
στην περίπτωση της διαχωριστικής επιφάνειας δύο
ομογενών και ισότροπων διηλεκτρικών (βλ. σχ. 2.11) |
|
όπου ![]() : μοναδιαίο διάνυσμα, κάθετο επί της επιφάνειας και με
φορά προς το εξωτερικό του αγωγού ή του διηλεκτρικού.
: μοναδιαίο διάνυσμα, κάθετο επί της επιφάνειας και με
φορά προς το εξωτερικό του αγωγού ή του διηλεκτρικού.
σ: επιφανειακή πυκνότητα πραγματικού
φορτίου.
ε1, ε2:
διηλεκτρικές σταθερές του διηλεκτρικού 1 και 2 αντίστοιχα.
![]() εφαπτομενική προς την διαχωριστική επιφάνεια
συνιστώσα της ηλεκτρικής έντασης διαταραχής από την πλευρά του διηλεκτρικού i (i = 1,2)
εφαπτομενική προς την διαχωριστική επιφάνεια
συνιστώσα της ηλεκτρικής έντασης διαταραχής από την πλευρά του διηλεκτρικού i (i = 1,2)
![]() κάθετη προς την διαχωριστική επιφάνεια
συνιστώσα της ηλεκτρικής έντασης/ διαταραχής από την πλευρά του διηλεκτρικού i
κάθετη προς την διαχωριστική επιφάνεια
συνιστώσα της ηλεκτρικής έντασης/ διαταραχής από την πλευρά του διηλεκτρικού i
![]() μέτρο της κάθετης
προς την διαχωριστική επιφάνεια συνιστώσας της ηλεκτρικής έντασης διαταραχής
από την πλευρά του διηλεκτρικού i, του οποίου το πρόσημο καθορίζεται με βάση την φορά του
διανύσματος
μέτρο της κάθετης
προς την διαχωριστική επιφάνεια συνιστώσας της ηλεκτρικής έντασης διαταραχής
από την πλευρά του διηλεκτρικού i, του οποίου το πρόσημο καθορίζεται με βάση την φορά του
διανύσματος ![]() : θετικό αν τα διανύσματα
: θετικό αν τα διανύσματα ![]() και
και ![]() έχουν την ίδια
φορά και αρνητικό στην αντίθετη περίπτωση.
έχουν την ίδια
φορά και αρνητικό στην αντίθετη περίπτωση.
Σχήμα 2.11 : Για την απόδειξη των συνοριακών συνθηκών της
Ηλεκτροστατικής.
Οι συνοριακές
συνθήκες της Ηλεκτροστατικής συμβάλλουν σημαντικά στην επίλυση πολλών
προβλημάτων, τα οποία σχετίζονται με τον προσδιορισμό του πεδίου ενός
συστήματος αγωγών ή/και διηλεκτρικών.
1°) Πόλωση
από μετατόπιση (ή εξ επαγωγής): Τα ηλεκτρικώς φορτισμένα σωματίδια, από
τα οποία αποτελούνται τα άτομα και τα μόρια, όταν δεχτούν την επίδραση ενός εξωτερικού πεδίου,
μετακινούνται. Η μετατόπιση τους αυτή,
έχει σαν αποτέλεσμα, την εμφάνιση διπολικής ροπής στα μη πολικά άτομα
και μόρια, και την αύξηση της ήδη υπάρχουσας στα πολικά μόρια (βλ. σχ.
2.20).
Σχήμα 2.20: Πόλωση από μετατόπιση a) μη πολικών, b) πολικών μορίων.
Η επαγόμενη διπολική ροπή ![]() ενός
ατόμου είναι - για όχι πολύ ισχυρά πεδία – ανάλογη προς την
ένταση τους:
ενός
ατόμου είναι - για όχι πολύ ισχυρά πεδία – ανάλογη προς την
ένταση τους:
![]() [2.29]
[2.29]
Ο συντελεστής α
ονομάζεται ατομική πολωσιμότητα, είναι ανεξάρτητος από την
θερμοκρασία και χαρακτηριστικός για το συγκεκριμένο άτομο.
Η επαγόμενη διπολική ροπή ενός μορίου είναι στην
γενική περίπτωση τανυστής 2ου μεγέθους.
2°) Πόλωση
από προσανατολισμό: Ορισμένα μόρια έχουν μόνιμη διπολική ροπή. Λόγω της
θερμικής κίνησης των μορίων οι διπολικές τους ροπές είναι προσανατολισμένες
στατιστικά, με αποτέλεσμα η συνολική διπολική ροπή κάθε μεγάλου αριθμού μορίων
να ισούται με μηδέν. Υπό την δράση όμως ενός εξωτερικού ηλεκτρικού πεδίου
ασκείται επί των μοριακών διπόλων μηχανική ροπή, η οποία τείνει να τα
προσανατολίσει κατά την διεύθυνση του. Ο
προσανατολισμός αυξάνεται με αυξανόμενη
ένταση του πεδίου και ελαττούμενη θερμοκρασία. Η κατ’ αυτό τον τρόπο
δημιουργούμενη διηλεκτρική πόλωση καλείται πόλωση από προσανατολισμό.
Ο
προσανατολισμός των μοριακών διπόλων απαιτεί κάποιον μετρήσιμο χρόνο για να
ολοκληρωθεί. Ο χρόνος αυτός αυξάνεται με τον συντελεστή ιξώδους του διηλεκτρικού,
και απειρίζεται στην περίπτωση των στερεών. Η παραπάνω καθυστέρηση στον
προσανατολισμό των μορίων χαρακτηρίζεται ως διηλεκτρική υστέρηση και είναι η πηγή των πολύ σπουδαίων
τεχνικά διηλεκτρικών απωλειών.
3°) Ιοντική πόλωση: Παρατηρείται
στα κρυσταλλικά εκείνα διηλεκτρικά, τα οποία σχηματίζουν ιοντικούς κρυστάλλους,
όπως π.χ. NaCl και CsCl. Είναι δε αποτέλεσμα της
μετακίνησης των θετικών και αρνητικών.
2.10.1Πόλωση χωρίς την επίδραση του εξωτερικού πεδίου. Πιεζοηλεκτρισμός
Ορισμένοι ιοντικοί κρύσταλλοι εμφανίζουν το
φαινόμενο του πιεζοηλεκτρισμού: Μηχανική παραμόρφωση (θλίψη,
ελκυσμός ή στρέψη) των παραπάνω κρυστάλλων σε συγκεκριμένες κατευθύνσεις έχει
σαν αποτέλεσμα την εμφάνιση ηλεκτρικών, επιφανειακών φορτίων, εξ αιτίας της
εμφάνισης ή μεταβολής της ήδη υπάρχουσας
διπολικής ροπής. Ιδιαίτερα έντονο εμφανίζουν το φαινόμενο του πιεζοηλεκτρισμού
ο χαλαζίας και η τουρμαλίνη.
Εφαρμογές: 1η) Πιεζοηλεκτρικοί κρύσταλλοι
χρησιμοποιούνται σαν ηλεκτρομηχανικοί
μεταποιητές στην Τεχνολογία Μετρήσεων: Οι πιεζοηλεκτρικές τάσεις είναι ευθέως ανάλογες
προς το αίτιο που τις προκαλεί .
2η)
Πιεζοηλεκτρικοί μηχανισμοί ανάφλεξης αερίων μειγμάτων χρησιμοποιούνται στους πιεζοηλεκτρικούς αναπτήρες, στις
μηχανές εσωτερικής καύσεως πολλών πλοιαρίων, χλοοκοπτών κ.λ.π.
3η)
Κρυσταλλικά μικρόφωνα και βελόνες γραμμοφώνου: Στα μεν πρώτα
έχουμε μετατροπή των ηχητικών κυμάτων ( ~ αυξομειώσεις πίεσης) , στις δε
δεύτερες της πίεσης που ασκείται από την κίνηση της βελόνης σε αντίστοιχα
μεταβαλλόμενες πιεζοηλεκτρικές τάσεις.
Το αντίστροφο
προς τον πιεζοηλεκτρισμό φαινόμενο έγκειται στην μεταβολή των διαστάσεων ενός
πιεζοηλεκτρικού κρυστάλλου υπό την επίδραση ηλεκτρικής τάσεως, και καλείται ηλεκτροσυστολή.
Εφαρμογές: 1η) Αν εφαρμόσουμε στα άκρα ενός
πιεζοηλεκτρικού κρυστάλλου εναλλασσόμενη τάση, ο κρύσταλλος εκτελεί εξαναγκασμένη
μηχανική ταλάντωση. Πρακτική αξιοποίηση
έχουμε στο μεγάφωνα υψηλών συχνοτήτων (10 ~ 16 kHz ) και κυρίως στην δημιουργία υπερήχων ( ν > 16 kHz).
2η) Από τα
σπουδαιότερα πιεζοηλεκτρικά υλικά είναι ο χαλαζίας (quartz). Εμφανίζει πολύ μικρούς θερμικούς
συντελεστές της συχνότητας των μηχανικών
ταλαντώσεων, τις οποίες εκτελεί. Το γεγονός αυτό σε συνδυασμό με την πολύ μικρή
απόσβεση των παραπάνω ταλαντώσεων οδήγησε στην κατασκευή των μεγάλης ακρίβειας
ωρολογίων χαλαζία.
Ηλεκτρικό ρεύμα καλείται κάθε κατευθυνόμενη
κίνηση ηλεκτρικών φορτίων.
Από όλες τις
περιπτώσεις ηλεκτρικού ρεύματος ιδιαίτερο πρακτικό ενδιαφέρον παρουσιάζει το
προκαλούμενο υπό την επίδραση ενός εξωτερικού ηλεκτρικού πεδίου. Αυτή την «ειδική» κατηγορία ηλεκτρικού
ρεύματος θα έχουμε υπόψη σε όλα τα επόμενα.
Ως ένταση i του ηλεκτρικού
ρεύματος ορίζεται το πηλίκο
του φορτίου dq, το οποίο διέρχεται από μία καθετή
προς την διεύθυνση ροής των φορτίων τομή του αγωγού μέσα σε χρόνο dt, προς τον (απειροστό) χρόνο dt:
ένταση του ηλ.
ρεύματος ![]() [ 3.1 ]
[ 3.1 ]
Μονάδα έντασης
στο SI : [ i] = A(mpere) :θεμελιώδη
μονάδα:
Ένα Ampere είναι η ένταση του
ρεύματος, το οποίο, όταν διαρρέει δύο ευθύγραμμους, παραλλήλους αγωγούς
πολύ μεγάλου μήκους, ευρισκόμενους σε απόσταση ενός μέτρου, προκαλεί δύναμη αλληλεπίδρασης
ίση με![]() ανά μονάδα μήκους των αγωγών.
ανά μονάδα μήκους των αγωγών.
Σαν φορά
του ηλεκτρικού ρεύματος ορίζεται
συμβατικά, η φορά κινήσεως των θετικών
υποτιθέμενων φορέων του φορτίου.
Όταν τόσο η
ένταση όσο και η φορά του ηλεκτρικού ρεύματος παραμένουν χρονικά αμετάβλητες,
το ρεύμα καλείται συνεχές ( D.C. –Direct Current), διαφορετικά μεταβαλλόμενο.
Από όλα τα είδη μεταβαλλόμενου ρεύματος ιδιαίτερο τεχνικό ενδιαφέρον παρουσιάζει
εκείνο, στο οποίο τόσο η ένταση όσο και η φορά μεταβάλλονται ημιτονοειδώς με
τον χρόνο. Το ρεύμα αυτό καλείται εναλλασσόμενο (Α.C. –Alternating Current).
ένταση συνεχούς
ρεύματος: ![]() [ 3.2 ]
[ 3.2 ]
όπου Q είναι το φορτίο το οποίο διέρχεται μέσα
σε χρόνο t μέσω μιας κάθετης
προς την διεύθυνση ροής των φορτίων διατομής του αγωγού.
Η ένταση του συνεχούς ρεύματος είναι η ίδια
σε όλες τις κάθετες διατομές ενός (μη διακλαδιζόμενου ) αγωγού.
Ρεύματα, των οποίων η ένταση - ενώ μεταβάλλεται χρονικά- είναι σε μία
δεδομένη χρονική στιγμή για όλες τις διατομές ενός μη διακλαδιζόμενου η ίδια ονομάζονται
στατικότροπα ή μόνιμα.
Εμείς θα
ασχοληθούμε μόνο με τέτοιου είδους μεταβαλλόμενα ρεύματα.
Φαινόμενο «επιδερμίδας» ( skin effect )
|
|
Όταν ένας αγωγός διαρρέεται από εναλλασσόμενο ρεύμα, αυτό δεν
κατανέμεται ομοιόμορφα καθ’ όλη την έκταση της διατομής του, αλλά (εξ αιτίας
του φαινομένου της «εσωτερικής αυτεπαγωγής») αυξάνεται από τον
πυρήνα του αγωγού προς την επιφάνειά του, στην οποία και περιορίζεται
ουσιαστικά σε υψηλές συχνότητες. Η παραπάνω «άπωση» του ρεύματος προς τα
εξωτερικά στρώματα του αγωγού χαρακτηρίζεται σαν «φαινόμενο επιδερμίδας».
Εφαρμογές: Για την μεταφορά υψηλόσυχνων ρευμάτων
χρησιμοποιούνται πολύκλωνα καλώδια και κοίλοι αγωγοί με λεπτά τοιχώματα,
ώστε το φαινόμενο της επιδερμίδας να περιορίζεται στο ελάχιστο.
Προκειμένου να έχουμε την δυνατότητα περιγραφής της
ακριβούς κατανομής του ρεύματος στα διάφορα σημεία της διατομής του αγωγού, εισάγουμε ένα νέο διανυσματικό μέγεθος, την
πυκνότητα ρεύματος ![]() :
:
πυκνότητα
ρεύματος: ![]() [
3.3 ]
[
3.3 ]
όπου di = ένταση του ρεύματος μέσω μιας στοιχειώδους
επιφάνειας ![]() .
.
Σύμφωνα λοιπόν
με την παραπάνω εξίσωση η ένταση i του ρεύματος μέσω μιας τυχαίας επιφάνειας S ισούται με την «ροή» της πυκνότητας ![]() του ρεύματος μέσω της εν λόγω επιφάνειας.
του ρεύματος μέσω της εν λόγω επιφάνειας.
Η πυκνότητα του συνεχούς ρεύματος είναι η ίδια σε όλα τα σημεία της
διατομής S ενός αγωγού:
πυκνότητα συνεχούς
ρεύματος: ![]() [
3.4 ]
[
3.4 ]
Από την
σταθερότητα επομένως της έντασης του συνεχούς ρεύματος σε όλες τις διατομές
ενός αγωγού προκύπτει, ότι η πυκνότητα
του συνεχούς ρεύματος σε δύο διαφορετικές διατομές ενός αγωγού είναι
αντιστρόφως ανάλογη προς το εμβαδόν τους:
![]() [
3.5 ]
[
3.5 ]
3.1.1 Σχέση μεταξύ πυκνότητας ρεύματος και ταχύτητας των φορέων φορτίου
Η πυκνότητα (και
κατ’ επέκταση και η ένταση του ) ρεύματος εξαρτάται από την ταχύτητα των φορέων φορτίου:
![]() : πυκνότητα
ρεύματος φορέων φορτίου Q [3.6]
: πυκνότητα
ρεύματος φορέων φορτίου Q [3.6]
όπου ![]() : μέση ταχύτητα φορέων φορτίου Q [3.7]
: μέση ταχύτητα φορέων φορτίου Q [3.7]
ρQ =
πυκνότητα φορτίου (λόγω φορέων φορτίου Q)
nk = αριθμητική πυκνότητα φορέων
ταχύτητας ![]()
NQ = αριθμητική πυκνότητα φορέων φορτίου Q ανεξαρτήτως
ταχύτητας
Σύμφωνα λοιπόν
με τις παραπάνω σχέσεις
η πυκνότητα (και κατ’ επέκταση και η ένταση του) ρεύματος εξαρτάται μόνον
από την μέση ταχύτητα των φορέων φορτίου, την καλούμενη και ταχύτητα μεταθέσεως. Σημειωτέον ότι
η φορά του διανύσματος της πυκνότητας καθορίζεται συμβατικά με βάση την
φορά μετάθεσης των θετικών φορέων.
Εφαρμογές: Υπολογισμός της ταχύτητας μεταθέσεως: Από την σχέση
[3.6] παίρνουμε για την ταχύτητα μεταθέσεως των κινουμένων φορτίων ![]() {1}. Στην
περίπτωση ενός μεταλλικού αγωγού ισχύει:
{1}. Στην
περίπτωση ενός μεταλλικού αγωγού ισχύει:
![]()
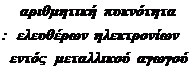 [3.8]
[3.8]
όπου d = πυκνότητα αγωγού (kg / m3 )
NA= 6,023×1026
άτομα/ kmol: αριθμός του Avogadro
K = αριθμός ελευθέρων
ηλεκτρονίων ανά άτομο
Μ = ατομική μάζα του αγωγού
Παράδειγμα: Για χάλκινο καλώδιο ( d = 8,96 ·
![]() {2}
{2}
Για μια λογική πυκνότητα
ρεύματος j =100 Α / cm2 , παίρνουμε για
την ταχύτητα μεταθέσεως των ελευθέρων ηλεκτρονίων εντός ενός
χάλκινου καλωδίου: ![]() .
.
Βλέπουμε λοιπόν,
ότι η μεγάλη ταχύτητα διάδοσης του ηλεκτρικού
ρεύματος δεν οφείλεται στην μετακίνηση των ηλεκτρονίων, αλλά στην (μεγάλη)
ταχύτητα διάδοσης του ηλεκτρικού πεδίου, η οποία ισούται με την ταχύτητα
διάδοσης του φωτός.
3.2 Αποτελέσματα του ηλεκτρικού ρεύματος
Θερμικά: Ένας ρευματοφόρος αγωγός
θερμαίνεται
Εφαρμογές: Αντιστάσεις
ηλεκτρικών θερμαστρών και εστιών, λαμπτήρες πυρακτώσεως κ.λ.π.
Μαγνητικά: Γύρω από έναν ρευματοφόρο αγωγό δημιουργείται μαγνητικό πεδίο.
Εφαρμογές:
Ηλεκτρομαγνήτες, ηλεκτρικές γεννήτριες, ηλεκτροκινητήρες κ.λ.π.
Χημικά: Η διέλευση του
ηλεκτρικού ρεύματος μέσω των καλουμένων αγωγών δευτέρας τάξεως[1] συνοδεύεται, από το φαινόμενο της ηλεκτρόλυσης.
Εφαρμογές:
Ηλεκτρομεταλλουργία, επιμετάλλωση κ.λ.π.
3.3 Όργανα μέτρησης του ηλ. ρεύματος
Η μέτρηση του
ρεύματος στηρίζεται στα αποτελέσματά
του.
Τα όργανα
μέτρησης της έντασης του ηλεκτρικού ρεύματος καλούνται γενικά αμπερόμετρα, εκείνα δε που
μετρούν πολύ μικρές εντάσεις ( » μΑ) γαλβανόμετρα. Οι πλέον διαδεδομένες στην πράξη μορφές είναι οι ακόλουθες:
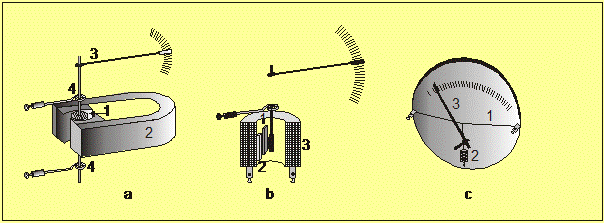
Σχήμα
3.3: Διάφοροι τύποι αμπερομέτρων.
Ηλεκτρική αντίσταση R ενός αγωγού (με την ευρύτερη
σημασία της λέξης) ή τμήματος αγωγού καλείται το πηλίκο της διαφοράς δυναμικού U μεταξύ των άκρων του αγωγού ή του τμήματός του προς την ένταση του
ρεύματος I, το οποίο τον ή το διαρρέει:
ηλεκτρική
αντίσταση: ![]() [
3 . 9 ]
[
3 . 9 ]
Το αντίστροφο
της ηλεκτρικής αντίστασης καλείται ηλεκτρική αγωγιμότητα:
ηλεκτρική αγωγιμότητα: ![]() [3 .10]
[3 .10]
|
Μονάδες (SI)
|
Σημειωτέον ότι
ο λόγος R=U/I ( και κατά συνέπεια και η ηλ. αγωγιμότητα G) εξαρτάται γενικώς από την τιμή της τάσης U και της έντασης I. Η σχέση μεταξύ έντασης I και τάσης U αποδίδεται
γραφικά με τις λεγόμενες χαρακτηριστικές
καμπύλες έντασης – τάσης:
α) Ωμικοί αγωγοί: Μέταλλα,
ηλεκτρολύτες, ημιαγωγοί, όταν η
θερμοκρασία είναι σταθερή:
|
|
Σχήμα 3.4: Χαρακτηριστική
καμπύλη έντασης-τάσης ενός ωμικού αγωγού και κύκλωμα μέτρησης. |
β) Ανορθωτική δίοδος:

Σχήμα 3.5: Χαρακτηριστική καμπύλη
έντασης-τάσης ενός ανορθωτικής διόδου και κύκλωμα μέτρησης.
γ) Δίοδος ηλεκτρονική λυχνία με κάθοδο πυρακτώσεως

Σχήμα 3.6: Χαρακτηριστική
καμπύλη έντασης- τάσης μιας διόδου ηλεκτρονικής λυχνίας και κύκλωμα μέτρησης.
δ) Φωτοβολταϊκό τόξο:

Σχήμα 3.7: Χαρακτηριστική
καμπύλη έντασης- τάσης ενός φωτοβολταϊκού τόξου και κύκλωμα μέτρησης.
Η ηλεκτρική αντίσταση ενός μεταλλικού
αγωγού είναι για σταθερή θερμοκρασία
ανεξάρτητη από την τάση, η οποία εφαρμόζεται στα άκρα του:
νόμος του Ohm: 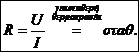 [3.11]
[3.11]
Αγωγοί, οι
οποίοι υπακούουν στον νόμο του Οhm καλούνται ωμικές αντιστάσεις. Στην
κατηγορία αυτή ανήκουν πλην των μετάλλων, οι ηλεκτρολύτες και οι ημιαγωγοί.
Για την
αντίσταση ενός μεταλλικού αγωγού προκύπτει η εξίσωση:
αντίσταση
μεταλλικού αγωγού: ![]() [3.12]
[3.12]
όπου l =
μήκος του αγωγού
S = διατομή του
αγωγού
Η
παράμετρος ρ καλείται ειδική αντίσταση.
Όταν στα άκρα ενός ομογενούς καλωδίου μήκους l εφαρμόζεται σταθερή τάση U, τότε στο
εσωτερικό του επικρατεί ένα ομογενές ηλεκτρικό πεδίο έντασης Ε=U/l.
→ ![]() [3.13]
[3.13]
νόμος
του Ohm μικροσκοπικά,
αν ρ και γ=σταθ. για σταθερή θερμοκρασία
όπου ![]() = πυκνότητα
ρεύματος
= πυκνότητα
ρεύματος
ρ = ειδική αντίσταση, γ = ειδική αγωγιμότητα.
3.4.2 Εξάρτηση της ειδικής αντίστασης από την θερμοκρασία
Η ειδική αντίσταση των μετάλλων αυξάνεται, ενώ των ημιαγωγών ελαττώνεται
με αυξανόμενη θερμοκρασία:
α) μέταλλα (για μικρές
σχετικά θερμοκρασιακές περιοχές) :
ρ = ρ0
(1+αt) [ 3.14]
ρ0 είναι ειδική
αντίσταση στους
α = θερμικός
συντελεστής αντιστάσεως.
β) ημιαγωγοί, έχουμε (συνήθως
εκθετική ρ~eT/A, Α = παράμετρος
εξαρτώμενη και από την φύση του ημιαγωγού, Τ = απόλυτη θερμοκρασία) ελάττωση
της ειδικής αντίστασης με αυξανόμενη θερμοκρασία.
Εφαρμογές: 1η) Η εξάρτηση της ηλεκτρικής
αντίστασης από την θερμοκρασία χρησιμοποιείται για την μέτρηση θερμοκρασιών.
2η) Κατασκευή των NTC - αντιστάσεων ( Negative Temperature Coefficient = αρνητικός
θερμικός συντελεστής) ή καυτών αγωγών, των οποίων η ηλεκτρική
αντίσταση ελαττώνεται με αυξανόμενη θερμοκρασία.
3.4.3 Εξάρτηση της ειδικής αντίστασης από άλλους παράγοντες - Εφαρμογές
α) Επίδραση μαγνητικού πεδίου έχει ως αποτέλεσμα
( συνήθως) την αύξηση της ειδικής αντίστασης.
β) Επίδραση ηλεκτρομαγνητικής ακτινοβολίας καταλλήλου
μήκους κύματος (συνήθως πρόκειται για ορατή, υπέρυθρη και υπεριώδη ακτινοβολία)
έχει ως αποτέλεσμα την εμφάνιση ή αύξηση της ήδη υπάρχουσας αγωγιμότητας
ορισμένων μονωτών και ημιαγωγών.
γ) Επίδραση μηχανικών παραμορφώσεων, τέλος, έχει
επίσης ως αποτέλεσμα την μεταβολή της ειδικής αντίστασης ορισμένων αγωγών,
γεγονός το οποίο εκμεταλλευόμαστε για την μέτρηση μικρών μεταβολών μήκους.
Σαν ηλεκτρικό
κύκλωμα χαρακτηρίζεται γενικά κάθε διαδρομή την οποία μπορεί να
ακολουθήσει ένα ηλεκτρικό ρεύμα, επειδή πρέπει συνήθως να είναι κλειστή.
Τα στοιχεία από τα οποία αποτελείται ένα
κύκλωμα διακρίνονται σε πηγές και καταναλωτές. Η λειτουργία μιας πηγής συνίσταται στην αναπλήρωση
της ηλεκτρικής ενέργειας, την οποία χάνουν τα φορτία κατά την ροή τους
μέσω των καταναλωτών, οι οποίοι τροφοδοτούνται από την πηγή, προκειμένου να
διατηρείται η ροή των φορτίων.
Χαρακτηριστικό
γνώρισμα κάθε πηγής αποτελεί η λεγόμενη ηλεκτρεγερτική δύναμη (ΗΕΔ):
ηλεκτρεγερτική
δύναμη (ΗΕΔ): ![]() [
3.15 ]
[
3.15 ]
Μονάδα μέτρησης της ΗΕΔ είναι το Volt.
Στα επόμενα
κεφάλαια χρησιμοποιήσουμε δε τους
ακόλουθους συμβολισμούς:
![]()
3.5.2 Συνδεσμολογίες αντιστάσεων
|
|
α) Σύνδεση
αντιστάσεων σε σειρά:
Στην σύνδεση σε σειρά η ένταση του ρεύματος είναι για όλες τις αντιστάσεις
η ίδια, ενώ η ολική τάση ισούται με το άθροισμα των επιμέρους τάσεων.
Επομένως η ολική αντίσταση R μιας συστοιχίας k αντιστάσεων
συνδεμένων σε σειρά ισούται με το άθροισμα των επιμέρους αντιστάσεων Ri της συστοιχίας:
ολική αντίσταση
συστοιχίας αντιστάσεων σε σειρά:
![]() [ 3.16 ]
[ 3.16 ]
β) Παράλληλη σύνδεση αντιστάσεων:
|
|
Στην παράλληλη σύνδεση η τάση Ui στα άκρα έκαστης αντίστασης Ri είναι η ίδια με την ολική τάση ![]() της συστοιχίας, ενώ το ρεύμα
της συστοιχίας, ενώ το ρεύμα ![]() , το οποίο διαρρέει την συστοιχία, ισούται
με το άθροισμα των ρευμάτων Ιi, τα οποία διαρρέουν τις επιμέρους αντιστάσεις της συστοιχίας.
, το οποίο διαρρέει την συστοιχία, ισούται
με το άθροισμα των ρευμάτων Ιi, τα οποία διαρρέουν τις επιμέρους αντιστάσεις της συστοιχίας.
Επομένως το αντίστροφο της ολικής αντίστασης μιας συστοιχίας
αντιστάσεων συνδεμένων παράλληλα ισούται, με το άθροισμα των αντιστρόφων
επιμέρους αντιστάσεων:
ολική αντίσταση
συστοιχίας αντιστάσεων παράλληλα: ![]() [3.17]
[3.17]
3.5.3 Ο ρόλος της εσωτερικής αντίστασης
Στο σχήμα 3.9
έχουμε την περίπτωση ενός κυκλώματος, το οποίο αποτελείται από μία μόνο πηγή
και μια ωμική αντίσταση. Ένα τέτοιο κύκλωμα χαρακτηρίζεται συνήθως ως απλό
κύκλωμα.
|
Σχήμα 3.9: Για τον ρόλο της εσωτερικής αντίστασης πηγής |
Η ένταση του
ρεύματος θα είναι :
![]() [3.18]
[3.18]
:ένταση του
ρεύματος σε απλό κύκλωμα
όπου Ε = ΗΕΔ της πηγής
r
= εσωτερική αντίσταση της πηγής
R = εξωτερική αντίσταση του κυκλώματος.
Η ένταση του
ρεύματος γίνεται μέγιστη και ίση με I = E/r (ρεύμα
βραχυκυκλώσεως), όταν βραχυκυκλώσουμε ( R = 0) τους πόλους της πηγής.
Η πολική τάση U ή τάση
ακροδεκτών θα είναι:
![]()
![]()
Επομένως η τάση ακροδεκτών μιας πηγής είναι πάντα μικρότερη
από την ΗΕΔ της πηγής, πλησιάζει όμως τόσο περισσότερο προς αυτήν όσο μικρότερη
είναι η εσωτερική από την εξωτερική αντίσταση.
 Συνδεσμολογία πηγών
Συνδεσμολογία πηγώνα) Σύνδεση σε σειρά:
Όπως φαίνεται
από το διπλανό σχήμα έχουμε:
|
|
πηγών σε σειρά [3.19] |
|
|
|
|
β) Σύνδεση παράλληλα: Οι ΗΕΔ και οι εσωτερικές αντιστάσεις
|
|
πηγών παράλληλα [3.20] |
|
|
όλων των πηγών πρέπει να είναι ίδιες!
γ) Μεικτή
σύνδεση: Και κατά την μεικτή σύνδεση πρέπει όλες
οι πηγές να είναι ίδιες.
|
|
μεικτής συνδεσμολογίας [3.21] |
|
|
Το ολικό ρεύμα Ιολ
και η τάση ακροδεκτών U+ - όλων των παραπάνω συστοιχιών είναι:
![]() ένταση
του ρεύματος και τάση ακροδεκτών [3.22]
ένταση
του ρεύματος και τάση ακροδεκτών [3.22]
Εολ = ολική
ΗΕΔ των πηγών του κυκλώματος
rολ = ολική εσωτερική αντίσταση των
πηγών του κυκλώματος
Rολ = ολική εξωτερική αντίσταση του κυκλώματος.
3.5.5 Κανόνες του Kirchhoff
Η μελέτη ενός
σύνθετου κυκλώματος γίνεται με την
βοήθεια των δύο κανόνων του Kirchhoff:
1ος κανόνας του Kirchhoff: Το άθροισμα των ρευμάτων, τα οποία φτάνουν σε έναν κόμβο,
ισούται με το άθροισμα των ρευμάτων, τα οποία φεύγουν από τον κόμβο αυτό.
Αν συμβατικά θεωρήσουμε ως θετικά τα ρεύματα που φθάνουν και αρνητικά
αυτά που φεύγουν, ο πρώτος κανόνας γράφεται:
1ος κανόνας του Kirchhoff: ![]() [3.23]
[3.23]
|
|
Παράδειγμα: Για τον διπλανό κόμβο ο 1ος κανόνας του Kirchhoff γράφεται: |
2ος κανόνας του Kirchhoff: Το άθροισμα των ΗΕΔ κατά μήκος ενός βρόγχου ισούται με το άθροισμα των πτώσεων
τάσης στις αντιστάσεις του βρόγχου:
2ος κανόνας του Kirchhoff: ![]() [3.24]
[3.24]
Καθορισμός προσήμου στον 2° κανόνα του Kirchhoff: Για κάθε βρόγχο επιλέγεται εντελώς
αυθαίρετα μια φορά ως θετική ( «φορά βρόγχου»). Όσες ΗΕΔ
θέλουν να δημιουργήσουν ρεύμα (συμβατικής!) φοράς ίδιας με την φορά βρόγχου θεωρούνται
θετικές, οι υπόλοιπες αρνητικές. Τέλος όσα ρεύματα έχουν (συμβατική!) φορά ίδια
με την φορά βρόγχου θεωρούνται θετικά, τα υπόλοιπα αρνητικά.
Παράδειγμα:
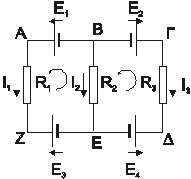 1ος
κ.K.: (κόμβος Β):
1ος
κ.K.: (κόμβος Β): ![]()
2ος
κ.K.: βρόγχος
ΑΒΕΖΑ: ![]()
“ ΒΓΔΕΒ: ![]()
” ΑΓΔΖΑ: ![]()
Μια σπουδαία
εφαρμογή των κανόνων του Kirchhoff είναι η μελέτη των λεγόμενων «γεφυρών», ειδικών
κυκλωμάτων τα οποία χρησιμοποιούνται για τον υπολογισμό αντιστάσεων. Η πιο
γνωστή γέφυρα είναι εκείνη του Wheatstone ( σχ. 3.11):
Μετακινώντας τον δρομέα Δ επί της χορδής («γέφυρα Wheatstone με χορδή») πετυχαίνουμε
την λεγόμενη ισορροπία της γέφυρας, κατά την οποία το γαλβανόμετρο Γ δεν
διαρρέεται από ρεύμα. Τότε έχουμε σύμφωνα με το 2ο κανόνα του Kirchhoff:
|
|
χορδή = ομογενής
{*}
(ρ = ειδική αντ., S = διατομή χορδής) |
|
Σχήμα 3.11: Γέφυρα
Wheatstone με χορδή. |
|
![]() [3.26]
[3.26]
Μετρώντας τα
μήκη απλώς l1 και l2 μπορούμε να
υπολογίσουμε την άγνωστη αντίσταση R1 με την βοήθεια της R2.
|
Σχήμα 3.12: Κύκλωμα RC. |
α) φόρτιση του
πυκνωτή (Ο διακόπτης στην θέση Α): Ο 2ος κανόνας του Kirchhoff για μια τυχαία
χρονική στιγμή t (0<t< ¥) μας δίνει:
![]() →
→ ![]() video5 [3.27]
video5 [3.27]
![]()
![]() video6 [3.27α]
video6 [3.27α]
![]()
![]() video7 [3.27β]
video7 [3.27β]
Η γραφική παράσταση
των παραπάνω εξισώσεων δίδεται στο σχήμα 3.13.
β) εκφόρτιση του πυκνωτή (ο διακόπτης
στην θέση Β, βλ. σχ. 3.12): Ο 2ος κανόνας του Kirchhoff μας δίνει:
0 < t < ¥![]() →
→ ![]() video8 [3.28]
video8 [3.28]
![]()
![]() video9 [3.28α]
video9 [3.28α]
![]()
![]() video10 [3.28β]
video10 [3.28β]
(Το
αρνητικό πρόσημο δηλώνει, ότι το ρεύμα κατά την εκφόρτιση έχει αντίθετη
φορά απ’ ότι κατά την φόρτιση)
Ο χρόνος t=RC είναι χαρακτηριστικός
για το κύκλωμα και καλείται σταθερή χρόνου.
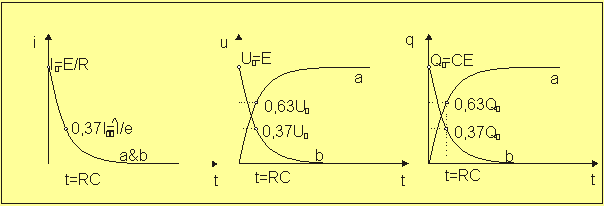
Σχήμα 3.13: Μεταβολή του ρεύματος i, της τάσης u και του φορτίου
q
σε κύκλωμα RC (
a=
φόρτιση, b=εκφόρτιση).
3.5.8 Ενέργεια και ισχύς του ηλ. ρεύματος
![]()
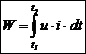 [3.29]
[3.29]
Αν το ρεύμα
είναι συνεχές, η παραπάνω σχέση
γίνεται:
![]() [3.30]
[3.30]
όπου W = ηλεκτρική ενέργεια η οποία δαπανάται
σε τμήμα κυκλώματος, στα άκρα του οποίου (τμήματος) εφαρμόζεται διαφορά δυναμικού
U και το οποίο διαρρέεται
από ρεύμα έντασης Ι.
Η αντίστοιχη ηλεκτρική ισχύς προκύπτει από την
γενική εξίσωση ορισμού (![]() ):
):
![]() [3.30α]
[3.30α]
Η παραπάνω
ηλεκτρική ενέργεια ( ή ισχύς) μετατρέπεται σε ισόποση ενέργεια (ή ισχύς) άλλης
μορφής, η οποία εξαρτάται από το είδος των καταναλωτών, οι οποίοι
παρεμβάλλονται στο συγκεκριμένο τμήμα του κυκλώματος. Στην περίπτωση που
πρόκειται για απλούς αντιστάτες
( º ωμικές
αντιστάσεις), η ηλ. ενέργεια (ή ισχύς) μετατρέπεται σε θερμότητα. Σύμφωνα δε με
τον νόμο του Ohm θα ισχύει:
![]() (Νόμος του Joule) [3.31]
(Νόμος του Joule) [3.31]
3.6.1 Αγωγιμότητα στερεών σωμάτων: αγωγοί, μονωτές, ημιαγωγοί.
Με βάση την
ηλεκτρική τους αγωγιμότητα τα στερεά σώματα διακρίνονται σε
ü
Αγωγούς (μέταλλα): είναι ωμικοί
αγωγοί, έχουν υψηλή ηλεκτρική αγωγιμότητα, η οποία ελαττώνεται με αυξανόμενη
θερμοκρασία, η ροή του ηλεκτρικού ρεύματος δεν συνοδεύεται από μεταφορά μάζας.
ü
Μονωτές: έχουν μηδενική
πρακτικά αγωγιμότητα, η οποία δεν εξαρτάται ουσιαστικά από την θερμοκρασία.
ü
Ημιαγωγούς: είναι συνήθως (όχι
όμως πάντα!) ωμικοί αγωγοί, έχουν μικρή έως μέση ηλεκτρική αγωγιμότητα, η οποία
αυξάνεται αισθητά με αυξανόμενη θερμοκρασία, η ροή του ηλεκτρικού ρεύματος δεν
συνοδεύεται από μεταφορά μάζας.
Οι παραπάνω,
πειραματικά κατοχυρωμένες, ιδιότητες εξηγούνται με την βοήθεια των ακολούθων
μοντέλων:
Μοντέλο των ελευθέρων ηλεκτρονίων (P.Drude και ο H.A. Lorentz): Tα ηλεκτρόνια
σθένους δεν ανήκουν σε κάποιο συγκεκριμένο άτομο, αλλά μπορούν και κινούνται
ελεύθερα μέσα σε όλο τον όγκο του κρυσταλλικού πλέγματος σχηματίζοντας ένα «νέφος
ελευθέρων ηλεκτρονίων».
Καθοριστικό ρόλο για το
μέγεθος της ειδικής αντίστασης ενός μεταλλικού αγωγού παίζουν οι
συγκρούσεις μεταξύ των ελευθέρων ηλεκτρονίων
και διαταραχών (ανωμαλιών) της
κρυσταλλικής δομής.
Τέτοιες
διαταραχές αποτελούν και οι θερμικές ταλαντώσεις του κρυσταλλικού πλέγματος,
οι οποίες αποτελούν στιγμιαίες
διαταραχές της περιοδικότητας. Οι θερμικές ταλαντώσεις αυξάνονται με
αυξανόμενη θερμοκρασία, γεγονός το οποίο εξηγεί και την αντίστοιχη αύξηση της
ειδικής αντίστασης.
Το μοντέλο των
ελευθέρων ηλεκτρονίων δεν μπορεί να εξηγήσει την διαφορά μεταξύ μετάλλων,
μονωτών και ημιαγωγών.
Μοντέλο των ενεργειακών ταινιών:
|
Σχήμα 3.14: Ενεργειακές ταινίες. |
Όπως προκύπτει από
τους νόμους της Κβαντομηχανικής τα ηλεκτρόνια ενός στερεού σώματος είναι
διατεταγμένα σε ενεργειακές ταινίες, οι οποίες χωρίζονται, μεταξύ τους
μέσω περιοχών στις οποίες απαγορεύεται να βρίσκεται η ενέργεια ενός ηλεκτρονίου
( «απαγορευμένες ζώνες» ή «ενεργειακά χάσματα»)
( βλ. σχ. 3.14).
|
Σχήμα 3.15: Ταινία σθένους και αγωγιμότητας. |
Η ανώτερη εντελώς
πλήρης ταινία καλείται ταινία (ή και ζώνη) σθένους,
ενώ η αμέσως από πάνω ευρισκόμενη ταινία/ζώνη αγωγιμότητας (βλ.
σχ. 3.15).
|
Σχήμα 3.16: Μοντέλο ενεργειακών ταινιών ενός
μονοσθενούς (α) και ενός δισθενούς (β) μετάλλου. |
1.
Μεταλλικοί αγωγοί:
Η αγωγιμότητα των μετάλλων οφείλεται στο γεγονός, ότι η ανώτατη κατειλημμένη
ταινία είτε δεν είναι πλήρης (βλ. σχ. 3.16β).
2.
Μονωτές: Στους μονωτές (βλ. σχ. 3.15) η ανώτατη
κατειλημμένη ταινία είναι πλήρης το δε ενεργειακό χάσμα που την χωρίζει από την
αμέσως ανώτερη είναι μεγαλύτερο από την δυνατή αύξηση της κινητικής ενέργειας
των ηλεκτρονίων μέσω θέρμανσης.
3.
Ημιαγωγοί: Ως ημιαγωγοί χαρακτηρίζονται τα υλικά
εκείνα, τα οποία σε πολύ χαμηλές θερμοκρασίες είναι μονωτές, η αγωγιμότητα
τους αυξάνεται όμως σημαντικά με αυξανόμενη θερμοκρασία.
3.6.1.1 Αυτοτελείς ημιαγωγοί - ιδιοαγωγιμότητα
Σαν «αυτοτελείς»
χαρακτηρίζονται οι πολύ καθαροί ημιαγωγοί.
Το γερμάνιο και
το πυρίτιο έχουν τέσσερα εξωτερικά ηλεκτρόνια. Κρυσταλλούνται κατά το κρυσταλλικό
πλέγμα του διαμαντιού, όπου κάθε άτομο περιβάλλεται από τέσσερα γειτονικά. Με
τον τρόπο αυτό κάθε άτομο έχει τέσσερις ισαπέχοντες γείτονες, με τους οποίους
και σχηματίζει ομοιοπολικό δεσμό, συμπληρώνοντας έτσι την επιθυμητή
οκτάδα ηλεκτρονίων, όπως φαίνεται και στο σχήμα 3.17.
|
Σχήμα 3.17: Δισδιάστατο μοντέλο του πλέγματος του διαμαντιού. |
Ο ζυγός αριθμός ηλεκτρονίων έχει σαν
αποτέλεσμα την πληρότητα των αντιστοίχων ενεργειακών ταινιών.
|
Σχήμα 3.18: Ενεργειακά χάσματα μεταξύ ταινίας σθένους και
αγωγιμότητας διαφόρων κρυστάλλων (στους Τ=0Κ). |
Λόγω της
πληρότητας των ενεργειακών ταινιών θα έπρεπε τα υλικά αυτά να είναι μονωτές,
πράγμα το οποίο και αληθεύει σε πολύ χαμηλές θερμοκρασίες. Όμως τα ηλεκτρόνια
σθένους δεν συγκρατούνται ισχυρά από στα
μεγάλα άτομα του πυριτίου και του γερμανίου. Έτσι αρκεί η θερμική κίνηση του πλέγματος για να ελευθερώσει
κάποια ηλεκτρόνια.
Ένα ηλεκτρόνιο,
το οποίο εγκαταλείπει τον συγκεκριμένο του δεσμό, αφήνει εκεί ένα πλεονάζον θετικό
φορτίο, το οποίο χαρακτηρίζεται σαν ηλεκτρονιακή
κενή θέση ή (θετική) οπή ( βλ. σχ. 3.19). Οι θετικές οπές
της ταινίας σθένους μπορούν να «κινούνται» μέσα στον όγκο του κρυστάλλου.
Μ
Επομένως η
ιδιοαγωγιμότητα (ή αυτοτελής
αγωγιμότητα) των ημιαγωγών οφείλεται, στην μετακίνηση ελευθέρων
ηλεκτρονίων και, θετικών οπών (στην ζώνη
σθένους).
Ο αριθμός των ελευθέρων ηλεκτρονίων (άρα και των οπών) αυξάνεται εκθετικά
με την θερμοκρασία, γεγονός το οποίο εξηγεί και την αντίστοιχη ελάττωση της ειδικής τους αντίστασης
(βλ. κεφ.3.4.2) με αυξανομένη
θερμοκρασία.
3.6.1.2 Ημιαγωγοί προσμίξεων τύπου n και p
Ιδιαίτερο
τεχνικό ενδιαφέρον παρουσιάζει η ελεγχόμενη ενσωμάτωση ξένων ατόμων σε κανονικές θέσεις του
κρυσταλλικού πλέγματος.
Η μέσω
ελεγχόμενης ενσωμάτωσης διαταραγμένοι ημιαγωγοί χαρακτηρίζονται ως ημιαγωγοί προσμίξεων ( τύπου n ή p):
Άτομα της πέμπτης
ομάδας του Περιοδικού Συστήματος (φωσφόρος/P, αρσενικό/As, αντιμόνιο/Sb) έχουν πέντε εξωτερικά
ηλεκτρόνια. Όταν ενσωματωθούν σε κανονικές
θέσεις του κρυσταλλικού πλέγματος του γερμανίου ή του πυριτίου, εμφανίζουν ένα
«πλεονασματικό» ηλεκτρόνιο ( βλ. σχ. 3.20).
Κάθε ενσωματωμένο άτομο της πέμπτης ομάδας προσφέρει πρακτικά ένα
ελεύθερο ηλεκτρόνιο και καλείται ως εκ τούτου δότης. Η αγωγιμότητα ενός ημιαγωγού με προσμίξεις
τύπου n (δηλαδή με
ενσωματωμένους δότες) χαρακτηρίζεται ως αγωγιμότητα
τύπου n, μια και
οφείλεται πρακτικά σε ελεύθερα
ηλεκτρόνια, δηλαδή αρνητικώς (negative) φορτισμένα σωματίδια.
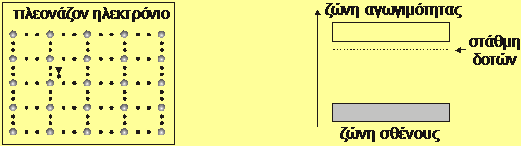
Σχήμα 3.20: Πλεονάζον
ηλεκτρόνιο (πεντασθενούς) δότη
ενσωματωμένου σε κρύσταλλο πυριτίου ή γερμανίου και (δεξιά) ενεργειακή
του στάθμη στο μοντέλο των ενεργειακών ταινιών.
Ακριβώς
αντίστροφη είναι η κατάσταση κατά την ενσωμάτωση ατόμων της τρίτης ομάδας
του Περιοδικού Συστήματος ( βόριο/Β, αλουμίνιο/Αl, γάλλιο/Ga και ίνδιο/In), τα οποία διαθέτουν τρία μόνον
εξωτερικά ηλεκτρόνια. Κάθε ενσωματωμένο
άτομο γίνεται πρακτικά αποδέκτης ενός γειτονικού ηλεκτρονίου και
κατά συνέπεια «δημιουργός» μιας θετικής οπής.
Για τον λόγο αυτό η αγωγιμότητα ενός ημιαγωγού με προσμίξεις τύπου p χαρακτηρίζεται ως αγωγιμότητα τύπου p. μια και οφείλεται πρακτικά σε θετικές (
positive) οπές.
Σχήμα 3.21 : Ελλιπές
ηλεκτρόνιο (τρισθενούς) αποδέκτη ("ο" ) ενσωματωμένου σε κρύσταλλο
πυριτίου ή γερμανίου και (δεξιά) ενεργειακή του στάθμη στο μοντέλο των
ενεργειακών ταινιών.
3.6.1.3 Εφαρμογές της μη αυτοτελούς (διαταραγμένης) αγωγιμότητας
1. Ανορθωτικές
δίοδοι με επαφή pn:
|
Σχήμα 3.23: Ορθά πολωμένη επαφή pn. |
Μια επαφή pn λειτουργεί σαν
μια βαλβίδα, η οποία επιτρέπει την διέλευση
του ρεύματος μόνο κατά την μία
φορά. Ένας τέτοιος κρύσταλλος λειτουργεί
επομένως ανορθωτικά και καλείται κρυσταλλοδίοδος (βλ.
και σχ. 3.25).
|
Σχήμα 3.24: Ανάστροφα πολωμένη επαφή pn. |
|
Σχήμα 3.25: Συμβολισμός
επαφής pn ως
(ανορθωτικής) διόδου και συνδεσμολογία κατά την (επιτρέπουσα την ροή
ρεύματος) ορθή φορά. |
2.
Φωτοδίοδοι –
φωτοστοιχεία: χρησιμοποιούνται ως φωτομετρητές και ως ηλεκτρικές
πηγές.
|
Σχήμα 3.25: Σχηματική παράσταση φωτοστοιχείου. |
Όταν επιδρά φως
επί της εσωτερικής επαφής, έχουμε ανύψωση ηλεκτρονίων στην ζώνη αγωγιμότητας
και επομένως δημιουργία οπών στην ζώνη σθένους. Τα μεν ηλεκτρόνια κατευθύνονται
(κάτω από την επίδραση της ![]() ) προς την ζώνη n, οι δε οπές προς την ζώνη p.
Έτσι το κύκλωμα του σχήματος 3.25 διαρρέεται από
ρεύμα.
) προς την ζώνη n, οι δε οπές προς την ζώνη p.
Έτσι το κύκλωμα του σχήματος 3.25 διαρρέεται από
ρεύμα.
|
Σχήμα 3.26: Σχηματική παράσταση και συμβολισμός μιας
ΝΡΝ - και μιας ΡΝΡ - κρυσταλλοτριόδου. |
3.
Κρυσταλλοτρίοδοι
(transistors) επαφής: Η
κρυσταλλοτρίοδος επαφής αποτελείται από έναν ημιαγώγιμο μονοκρύσταλλο, στον
οποίο γειτονεύουν (απόσταση » 1 μm) δύο επαφές pn.
|
Σχήμα 3.27: Εξήγηση της λειτουργίας μιας (ΝΡΝ-) κρυσταλλοτριόδου. |
Η ορθά πολωμένη επαφή pn καλείται εκπομπός
Ε,
η ανάστροφα πολωμένη επαφή pn καλείται συλλέκτης
C,
η περιοχή μεταξύ των δύο επαφών καλείται ( για ιστορικούς -
κατασκευαστικούς λόγους βάση Β.
τΤο διαρρέον το κύκλωμα εκπομπού - (βάσης ρεύμα ελέγχει εκείνο
του κυκλώματος συλλέκτη - βάσης. Η κρυσταλλοδίοδος (transistor) επαφής μπορεί να λειτουργήσει ως ενισχυτής ισχύος.
Η συνδεσμολογία
του σχ. 3.27, κατά την οποία η βάση αποτελεί τον κοινό ακροδέκτη, είναι
γνωστή ως συνδεσμολογία κοινής βάσης.
Στην πράξη
επιλέγεται συνήθως η συνδεσμολογία κοινού εκπομπού ( σχ. 3.28). Κατά την συνδεσμολογία κοινού εκπομπού η
κρυσταλλοτρίοδος λειτουργεί ως ενισχυτής ρεύματος.
|
Σχήμα 3.28: Συνδεσμολογία κοινού
εκπομπού. |
|
Πίνακας 3.6.2.1: Κρίσιμη θερμοκρασία
ορισμένων υπεραγωγών σε βαθμούς Κ |
|||
|
Zn |
0,9 |
NbN |
16 |
|
In |
3,4 |
V3Si |
17,1 |
|
Sn |
3,7 |
Nb3Al |
17,5 |
|
Pb |
7,2 |
Nb3Sn |
18,5 |
|
Nb |
9,2 |
Nb3Ge |
23,2 |
|
NbC |
10 |
Bi2Sr2Ca2Cu3O10 |
110 |
|
La3Li |
10,4 |
Te2Ca2Ba2Cu3Ox |
135 |
3.6.2 Υπεραγωγιμότητα
Η ηλεκτρική
αντίσταση ορισμένων μετάλλων, κραμάτων και ημιαγωγών (σχεδόν) μηδενίζεται, όταν
αυτά ψυχθούν κάτωθεν μιας, χαρακτηριστικής για το συγκεκριμένο υλικό, κρίσιμης
θερμοκρασίας. Το φαινόμενο αυτό, γνωστό ως υπεραγωγιμότητα.
|
Σχήμα 3.29: Φαινόμενο Meißner - Ochsenfeld. |
α) Υπεραγωγοί 1ου
είδους («μαλακοί»
υπεραγωγοί):
Σε μία
συγκεκριμένη κρίσιμη ένταση («κρίσιμο πεδίο»)
Βκ έχουμε ακαριαία μετάβαση στην κανονικά αγώγιμη κατάσταση.
Φαινόμενο Meissner – Ochsenfeld: Κατά την ψύξη ενός υπεραγωγού 1ου είδους
κάτωθεν μιας κρίσιμης θερμοκρασίας
έχουμε εκτοπισμό του μαγνητικού πεδίου από το εσωτερικό του αγωγού (βλ.
σχ. 3.29).
|
Σχήμα 3.30: Ένταση του μαγνητικού πεδίου στο εσωτερικό
ενός υπεραγωγού 1ου (αριστερά) και 2ου (δεξιά) είδους σε συνάρτηση από την
τιμή του εξωτερικού πεδίου. |
β) Υπεραγωγοί 2ου είδους («σκληροί»
υπεραγωγοί): Δεν έχουμε ακαριαία
μετάβαση στην κανονικά αγώγιμη κατάσταση, όταν το εξωτερικό πεδίο πάρει
μια κρίσιμη ένταση, όπως συμβαίνει στην περίπτωση ενός υπεραγωγού πρώτου
είδους. Αλλά όταν η ένταση του μαγνητικού πεδίου ξεπεράσει μια κρίσιμη τιμή Βκ1
, αρχίζει το πεδίο να διεισδύει σιγά-σιγά στο εσωτερικό του αγωγού, τον οποίο
όμως διαρρέει εντελώς, μόνον όταν η ένταση του ξεπεράσει μια (σε μερικές
περιπτώσεις σημαντικά μεγαλύτερη) κρίσιμη τιμή Βκ2 , οπότε και εξαφανίζεται
η υπεραγωγιμότητα (βλ. σχ. 3.30).
Δημιουργία
πανίσχυρων μαγνητικών πεδίων: Στο εμπόριο κυκλοφορούν ήδη υπεραγώγιμα
σωληνοειδή, με τα οποία μπορούν να επιτευχθούν μαγνητικά πεδία έντασης
μεγαλύτερης των 10 Τesla, ενώ σε εργαστηριακές συνθήκες έχουν δημιουργηθεί πεδία μέχρι και 51 Τ.
Υπεραγώγιμα
σωληνοειδή χρησιμοποιούνται ως υπερμαγνήτες σε επιταχυντές σωματιδίων, για
την μαγνητική θωράκιση διαστημοπλοίων καθώς και για την συγκράτηση του
πλάσματος σε πειράματα που επιδιώκουν την ελεγχόμενη θερμοπυρηνική σύντηξη.
Τέλος η κατάρρευση της υπεραγωγιμότητας μέσω ενός μαγνητικού πεδίου χρησιμοποιείται για την κατασκευή διακοπτών
και στοιχείων μνήμης ( «κρύοτρα ») σε υπερυπολογιστές.
Υγροί αγωγοί είναι τα (υδατικά κυρίως) διαλύματα
των οξέων, βάσεων και αλάτων καθώς και τα τήγματα βάσεων, αλάτων και
μετάλλων.
|
Σχήμα 3.31: Για την μελέτη της ηλεκτρολυτικής
αγωγιμότητας. |
Φορείς του ηλεκτρικού
ρεύματος στα υγρά είναι συνήθως θετικά και αρνητικά ιόντα· εξαίρεση
αποτελούν τα τήγματα μετάλλων, των οποίων η αγωγιμότητα οφείλεται στο γνωστό
μας ηλεκτρονικό νέφος. Όλα τα υπόλοιπα δεν αφορούν τα τήγματα μετάλλων.
Οι φορείς του
ηλεκτρικού ρεύματος προκύπτουν μέσω της διάσπασης των μορίων σε ιόντα, η οποία
χαρακτηρίζεται ως ηλεκτρολυτική διάσταση. Η ηλεκτρολυτική διάσταση
είναι αποτέλεσμα:
ü
στα τήγματα των βάσεων και των αλάτων της
διάσπασης του κρυσταλλικού πλέγματος στα αυτό αποτελούντα ιόντα μέσω αύξησης
της θερμικής τους κίνησης.
ü
στα υδατικά διαλύματα των βάσεων και των αλάτων της
παρεμβολής των ισχυρώς πολικών μορίων του νερού μεταξύ των ιόντων του κρυσταλλικού
πλέγματος, η οποία έχει σαν αποτέλεσμα την εξασθένηση των δυνάμεων Coulomb μεταξύ των
ιόντων του πλέγματος.
ü
στα υδατικά διαλύματα των οξέων της απόσπασης πρωτονίων (Η+) από τα
μόρια του νερού, οπότε σχηματίζονται οξόνια (Η3Ο+)
Στο εξωτερικό κύκλωμα του βολταμέτρου, έχουμε ροή
ηλεκτρονίων στο δε αγώγιμο υγρό ροή ιόντων.
Επιπλέον, η ροή του ρεύματος συνοδεύεται από το φαινόμενο της
ηλεκτρόλυσης: της έκλυσης ή εναπόθεσης συστατικών του υγρού ή προϊόντων
δευτερευουσών αντιδράσεων παρά των
ηλεκτροδίων. Για τον λόγο αυτό και οι ουσίες (οξέα, βάσεις και άλατα), των
οποίων τα διαλύματα ή τήγματα άγουν τον ηλεκτρισμό, χαρακτηρίζονται ως ηλεκτρολύτες.
Πολλές φορές παρά των ηλεκτροδίων έχουμε δευτερεύουσες
αντιδράσεις μεταξύ των ιόντων, των ηλεκτροδίων ή/και του διαλύτη.
3.6.4.1 Νόμοι της ηλεκτρόλυσης (Faraday)
1ος νόμος του Faraday: η μάζα m της παρά των ηλεκτροδίων ηλεκτρολυτικά ελευθερούμενης ουσίας είναι ανάλογη
του φορτίου Q, το οποίο μετακινείται μέσω του
ηλεκτρολύτου:
![]() [3.32]
[3.32]
όπου Ι = ένταση του (συνεχούς
εννοείται) ρεύματος
t = χρόνος ροής του ρεύματος
Η σταθερή
αναλογίας Α καλείται ηλεκτροχημικό
ισοδύναμο της αντίστοιχης ουσίας και ισούται με την ανά μονάδα φορτίου ελευθερούμενη μάζα.
2ος νόμος του Faraday: η ελευθέρωση ηλεκρολυτικώς ποσότητας ίσης με ένα γραμμοϊσοδύναμο
συνεπάγεται πάντα την μετακίνηση φορτίου
![]() (σταθερή
Faraday)
(σταθερή
Faraday)
ανεξάρτητα από το είδος της ουσίας.
Από τον 2ο
νόμο προκύπτει: ![]() [3.33]
[3.33]
(Α = ηλεκτροχημικό ισοδύναμο)
Συνδυάζοντας τις
παραπάνω σχέσεις παίρνουμε τον γενικευμένο
νόμο του Faraday:
![]() [3.34]
[3.34]
όπου m = μάζα της παρά
των ηλεκτροδίων ηλεκτρολυτικά ελευθερούμενης ουσίας
Σ = σθένος του ιόντος της ουσίας πριν την αποφόρτιση του
παρά των ηλεκτρόδιων
F = σταθερή του Faraday
Από τον πρώτο
νόμο του Faraday προκύπτει άμεσα
η ακόλουθη πρόταση:
Οι μάζες m1 και m2 των ουσιών, οι οποίες
ελευθερώνονται κατά την ηλεκτρόλυση δύο διαφορετικών ηλεκτρολυτών μέσω της
διέλευσης του ίδιου ηλεκτρικού φορτίου συμπεριφέρονται όπως τα
ηλεκτροχημικά τους ισοδύναμα:
m1 / m2 =
A1 / A2 [
3.35 ]
3.6.4.2 Ηλεκτρολυτική αγωγιμότητα
Όταν σε ένα
ηλεκτρολυτικό διάλυμα επικρατεί ένα ομογενές ηλεκτροστατικό πεδίο έντασης Ε, κάθε ιόν δέχεται την επίδραση μιας σταθερής
δύναμης ![]() , όπου
, όπου ![]() το φορτίο του
ιόντος. Κάτω από την επίδραση της σταθερής αυτής δύναμης το ιόν δεν διαγράφει
επιταχυνόμενη κίνηση, αλλά αποκτά μια σταθερή οριακή ταχύτητα u:
το φορτίο του
ιόντος. Κάτω από την επίδραση της σταθερής αυτής δύναμης το ιόν δεν διαγράφει
επιταχυνόμενη κίνηση, αλλά αποκτά μια σταθερή οριακή ταχύτητα u:
![]() [3.36]
[3.36]
όπου κ
= η ευκινησία του ιόντος.
Στην περίπτωση
ενός ηλεκτρολύτου έχουμε δύο είδη ιόντων, τα οποία συμμετέχουν στην μεταφορά
φορτίου, οπότε στην θέση της [ 3.36 ] θα έχουμε τις ακόλουθες δύο εξισώσεις:
![]() [3.36α]
[3.36α]
![]() [3.36β]
[3.36β]
Οι ευκινησίες κ+
και κ- είναι γενικά διαφορετικές μεταξύ τους.
Εάν συμβολίσουμε με n+ και n- τις αριθμητικές
πυκνότητες, και με Σ+ και Σ-
τα σθένη των κατιόντων και ανιόντων αντίστοιχα,
τότε παίρνουμε τις ακόλουθες πυκνότητες ρεύματος:
|
|
[3.37] |
|
|
όπου γ+
και γ_ οι ειδικές αγωγιμότητες
των κατιόντων και ανιόντων, αντίστοιχα.
Για την ολική επομένως
πυκνότητα ρεύματος παίρνουμε:
![]() [3.38]
[3.38]
Βλέπουμε λοιπόν
ότι η (ειδική)
αγωγιμότητα ενός ηλεκτρολύτου είναι ανάλογη προς τα σθένη, τις αριθμητικές
πυκνότητες και τις ευκινησίες των κατιόντων και ανιόντων.
Για τον λόγο
αυτό η αγωγιμότητα των ηλεκτρολυτών εξαρτάται
επιπλέον από την συγκέντρωση του συγκεκριμένου ηλεκτρολυτικού διαλύματος καθώς
και τον βαθμό διάστασης. Η ακριβής εξάρτηση είναι αρκετά πολύπλοκη.
Εκείνο, το οποίο ισχύει γενικά, είναι, ότι η
ηλεκτρική αγωγιμότητα των ηλεκτρολυτών αυξάνει με αυξανόμενη
θερμοκρασία.
3.6.4.3 Εφαρμογές της ηλεκτρόλυσης
α) Βιομηχανική
παραγωγή διαφόρων ουσιών.
β) Βιομηχανικός
καθαρισμός διαφόρων μετάλλων από προσμίξεις.
γ) Επιμετάλλωση
αντικειμένων με σκοπό την προστασία τους ή την καλαισθητοποίηση τους.
(επινικέλωση, επιχάλκωση, επιχρωμίωση, επιψευδαργύρωση, επιχρύσωση και επαργύρωση)
γ) Γαλβανοπλαστική (από τον L. Galvani): ονομάζεται η
αναπαραγωγή αντιγράφων διαφόρων αντικειμένων, όπως μεταλλίων, νομισμάτων,
τυπογραφικών πλακών, δίσκων γραμμοφώνου.
δ) Ηλεκτρολυτική
στίλβωση επιφανειών.
ε) Ανοδική
οξείδωση: επικάλυψη της επιφάνειας ενός μεταλλικού αντικειμένου
μέσω στρώματος οξειδίου.
3.6.4.4 Ηλεκτροχημικά στοιχεία – τάση επαφής μεταξύ μετάλλου και ηλεκτρολύτη
Όταν βυθίσουμε ένα
μέταλλο μέσα σ’ έναν ηλεκτρολύτη, τότε ο
μεν ηλεκτρολύτης να φορτίζεται θετικά το δε μέταλλο αρνητικά. Έτσι μεταξύ
μετάλλου και διαλύματος αρχίζει να δημιουργείται μια τάση, η οποία αντιτίθεται
στην παραπέρα μετάβαση θετικών ιόντων από το μέταλλο στο διάλυμα. (τάση
επαφής)
Αν βυθίσουμε δύο
διαφορετικά μεταλλικά ηλεκτρόδια σ’ ένα ηλεκτρολυτικό διάλυμα,
τότε μεταξύ έκαστου ηλεκτροδίου και του ηλεκτρολύτη αναπτύσσεται η αντίστοιχη
τάση επαφής. Η τάση αυτή μεταξύ των δύο
ηλεκτροδίων έχει σαν αποτέλεσμα την διέλευση ηλεκτρικού ρεύματος μέσω ενός
αγωγού, ο οποίος συνδέει τα δύο ηλεκτρόδια μεταξύ τους. Επομένως μια διάταξη
αποτελούμενη από δύο διαφορετικά μέταλλα («μεταλλικά ηλεκτρόδια») βυθισμένα
εντός ενός ηλεκτρολύτη λειτουργεί ως ηλεκτρική πηγή και ονομάζεται βολταϊκό
στοιχείο (κοινώς μπαταρία).
Στα βολταϊκά λοιπόν στοιχεία
έχουμε μετατροπή χημικής σε ηλεκτρική ενέργεια εξ ου και ο
χαρακτηρισμός τους και ως ηλεκτροχημικά στοιχεία
3.6.4.5 Πόλωση των ηλεκτροδίων
Η αλλοίωση της φύσεως της επιφάνειας επαφής
μεταξύ ηλεκτροδίων και ηλεκτρολύτη λόγω ηλεκτροχημικών αντιδράσεων καλείται πόλωση των ηλεκτροδίων.
Στην
περίπτωση ενός βολταϊκού στοιχείου μέσω
της πολώσεως των ηλεκτροδίων δημιουργείται αντιηλεκτρεγερτική δύναμη, η οποία
τείνει να μηδενίσει την αρχικώς μεταξύ των ηλεκτροδίων επικρατούσα τάση. Ως εκ
τούτου η πόλωση των ηλεκτροδίων ενός βολταϊκού στοιχείου είναι ανεπιθύμητη και
εμποδίζεται με αντιπολωτικά μέσα..
Πόλωση των ηλεκτροδίων
έχουμε και κατά την ηλεκτρόλυση και έχει ως αποτέλεσμα την μείωση του
ρεύματος.
Το φαινόμενο της πόλωσης των ηλεκτροδίων,
επιτρέπει από την άλλη την δημιουργία πολύ χρήσιμων, επαναφορτιζομένων
ηλεκτρικών πηγών, οι οποίες χαρακτηρίζονται ως συσσωρευτές: Δύο
αρχικώς όμοια ηλεκτρόδια καθίστανται ανόμοια,
μέσω πόλωσης κατά την φόρτιση του συσσωρευτή, οπότε
έχουμε μετατροπή ηλεκτρικής
ενέργειας σε χημική. Κατά την
εκφόρτιση του συσσωρευτή μέσω σύνδεσης με εξωτερικό κύκλωμα έχουμε μετατροπή
της αποταμειευθείσας χημικής ενέργειας σε ηλεκτρική.
Παραδείγματα ηλεκτροχημικών στοιχείων και συσσωρευτών:
|
Σχήμα 3.33: Το ξερό στοιχείο του εμπορίου σχηματικά. |
α) Το ξηρό στοιχείο του εμπορίου:
Ως ηλεκτρολύτης χρησιμοποιείται υδατικό διάλυμα χλωριούχου αμμωνίου
(NH4Cl), το οποίο
αναμιγνύεται με ρινίσματα ξύλου προκειμένου να καταστεί παχύρρευστο («ξηρό»),
ώστε η χρήση του στοιχείου να μην συνοδεύεται από διαρροές. Μέσα στον ηλεκτρολύτη
είναι βυθισμένο το θετικό ηλεκτρόδιο (βλ. σχ. 3.33), το οποίο αποτελείται από
άνθρακα (C), και περιβάλλεται
από αντιπολωτικό υπεροξείδιο του μαγγανίου (MnO2). Το αρνητικό
ηλεκτρόδιο αποτελείται από ψευδάργυρο (Zn) και είναι διαμορφωμένο έτσι, ώστε να
αποτελεί συγχρόνως και το περίβλημα του στοιχείου.
Η ΗΕΔ του στοιχείου ανέρχεται σε 1,5 Volts.
β) Ο συσσωρευτής μολύβδου αποτελείται από
κατάλληλο δοχείο, το οποίο περιέχει διάλυμα θειικού οξέος (H2SO4), εντός του οποίου είναι βυθισμένα δύο συστήματα
πλακών, από μόλυβδο (Pb) και διοξείδιο του μολύβδου (PbO2), τα οποία αποτελούν
το αρνητικό και θετικό ηλεκτρόδιο αντίστοιχα.
Όταν τα δύο
ανόμοια ηλεκτρόδια (πόλοι) του συσσωρευτή συνδεθούν με εξωτερικό κύκλωμα (βλ.
σχ.3.34), ο συσσωρευτής λειτουργεί ως πηγή ηλεκτρικού ρεύματος, κατά την
διάρκεια του οποίου πραγματοποιούνται οι ακόλουθες χημικές αντιδράσεις:
εκφόρτιση:
αρνητικό
ηλεκτρόδιο: ![]()
θετικό
ηλεκτρόδιο: ![]()
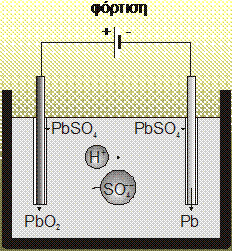
Σχήμα 3.34: Εκφόρτιοη και
φόρτιση συσσωρευτού μολύβδου σχηματικά.
Τα δύο αρχικώς ανόμοια
ηλεκτρόδια τείνουν να εξομοιωθούν κατά την εκφόρτιση, ενώ συγχρόνως δαπανάται
θειικό οξύ με αποτέλεσμα την αραίωση του διαλύματος.
Αν συνδέσουμε
τον συσσωρευτή με εξωτερική πηγή (βλ. σχ. 3.34), οι παραπάνω χημικές αντιδράσεις
αντιστρέφονται, με αποτέλεσμα την αποθήκευση μέρους της προσφερόμενης από την
πηγή ηλεκτρικής ενέργειας υπό μορφή χημικής:
φόρτιση:
κάθοδος (-): ![]()
άνοδος (+): ![]()
Λόγω των
παραπάνω αντιδράσεων, τα ηλεκτρόδια καθίστανται εκ νέου ανόμοια, ενώ παράγεται
θειικό οξύ, οπότε το διάλυμα ξαναπυκνώνει.
3.6.5 Θερμοηλεκτρικό φαινόμενο
Προκειμένου να
απομακρύνουμε ένα «ελεύθερο» ηλεκτρόνιο από ένα μέταλλο πρέπει να του
προσφέρουμε το λεγόμενο έργο εξόδου
Το έργο εξόδου εξαρτάται
από την φύση του μετάλλου και μπορεί να
προσφερθεί με διάφορους τρόπους:
α) με μορφή
ηλεκτρομαγνητικής ακτινοβολίας, οπότε το φαινόμενο της εξόδου χαρακτηρίζεται
ως φωτοεκπομπή.
β) με θέρμανση ![]() θερμιονική εκπομπή.
θερμιονική εκπομπή.
γ) με επίδραση
ηλεκτρικού πεδίου ![]() εκπομπή πεδίου
εκπομπή πεδίου
δ) με βομβαρδισμό
σωματιδίων ![]() εκπομπή κρούσεως.
εκπομπή κρούσεως.
Όταν δύο
μέταλλα έλθουν σε επαφή, τότε πολλά από
ελεύθερα ηλεκτρόνια, τα οποία μεταπηδούν - λόγω
στατιστικώς αυξημένης θερμικής ενέργειας από το μέταλλο με το μικρότερο
σ’ εκείνο με το μεγαλύτερο έργο εξόδου, «παγιδεύονται σ’ αυτό. Έτσι μεταξύ των
δύο μετάλλων εμφανίζεται διαφορά δυναμικού, η λεγόμενη τάση επαφής.
Παρ’ όλα ταύτα, αν συνδέσουμε τα δύο μέταλλα σε ένα κλειστό κύκλωμα (![]() δύο επαφές / βλ. σχ.3.35) δεν έχουμε ηλεκτρικό ρεύμα
επειδή οι δύο τάσεις επαφής είναι ίσες και αντίθετες.
δύο επαφές / βλ. σχ.3.35) δεν έχουμε ηλεκτρικό ρεύμα
επειδή οι δύο τάσεις επαφής είναι ίσες και αντίθετες.
Γενικεύοντας
παίρνουμε το νόμο του
Σε κάθε κλειστό κύκλωμα αποτελούμενο από διάφορα μέταλλα ή κράματα μετάλλων
το άθροισμα των τάσεων επαφής ισούται με μηδέν, όταν όλες οι επαφές έχουν την
ίδια θερμοκρασία.

Σχήμα
3.35: Όταν οι δύο επαφές έχουν την ίδια
θερμοκρασία (αριστερά) δεν έχουμε ρεύμα, αν όμως οι δύο επαφές έχουν διαφορετική
θερμοκρασία (δεξιά), τότε έχουμε ρεύμα εξαιτίας της θερμοηλεκτρικής τάσης.
Αν οι επαφές
έχουν διαφορετικές θερμοκρασίες, τότε η τάση της θερμότερης επαφής είναι
μεγαλύτερη. Μεταξύ των δύο επαφών επικρατεί διαφορά δυναμικού, η οποία καλείται
θερμοηλεκτρική τάση και ισούται με την διαφορά των δύο τάσεων
επαφής. Λόγω της θερμοηλεκτρικής αυτής τάσης το κύκλωμα των δύο μετάλλων
διαρρέεται από ρεύμα και καλείται θερμοστοιχείο.
Το φαινόμενο της
εμφάνισης της θερμοηλεκτρικής τάσης μεταξύ των επαφών δύο διαφορετικών μετάλλων,
όταν οι επαφές έχουν διαφορετική θερμοκρασία, καλείται θερμοηλεκτρικό φαινόμενο ή φαινόμενο Seebeck.
Η θερμοηλεκτρική
τάση ![]() εξαρτάται μόνο από
την θερμοκρασία των δύο επαφών και το ζεύγος των μετάλλων. Για πολλά ζεύγη μετάλλων η εξάρτηση της θερμοηλεκτρικής τάσης από την
θερμοκρασία είναι (σχεδόν) γραμμική
εξαρτάται μόνο από
την θερμοκρασία των δύο επαφών και το ζεύγος των μετάλλων. Για πολλά ζεύγη μετάλλων η εξάρτηση της θερμοηλεκτρικής τάσης από την
θερμοκρασία είναι (σχεδόν) γραμμική
![]() [3.39]
[3.39]
Ο συντελεστής κ
(το πηλίκο δηλαδή της θερμοηλεκτρικής τάσης προς την διαφορά θερμοκρασίας ΔΤ
μεταξύ των δυο επαφών) καλείται θερμοδύναμη.
|
Πίνακας 3.6.4β: Τιμές θερμοδύναμης διαφόρων θερμοστοιχείων |
|||
|
Θερμοστοιχείο |
κ(μV/K) |
ΔΤ(°C) |
μέγιστη
θερμοκρασία επαφής |
|
Χαλκός/Κονσταντάνη |
42,5 |
0 ~ 100 |
+ |
|
Σίδηρος/Κονσταντάνη |
53,7 |
0 ~ 200 |
+ |
|
Νίκελιο/Χρωμιονικέλιο |
41,3 |
0 ~ 1000 |
+ |
|
Πλάτινα/Πλατίνα-Ρόδιο |
9,6 |
0 ~ 1000 |
+ |
|
Ιρίδιο/Ιρίδιο - Ρήνιο |
17 |
0 ~ 2000 |
+ |
Εφαρμογές: Μέτρηση
θερμοκρασιών και κατασκευή θερμογενντριών.
3.6.5.1 Φαινόμενο Peltier
|
Σχήμα 3.36: Στοιχείο Peltier. |
Το
φαινόμενο Peltier είναι η αντιστροφή του θερμοηλεκτρικού φαινομένου: Όταν
το κύκλωμα του σχήματος 3.36 («στοιχείο Peltier») διαρρέεται από
ρεύμα, τότε μεταξύ των δύο επαφών των μετάλλων Α και Β αναπτύσσεται διαφορά
θερμοκρασίας.
Η απαγόμενη στην ψυχόμενη επαφή θερμότητα Q δίδεται από την σχέση:
![]() [3.40]
[3.40]
όπου Π = «συντελεστής
Peltier ». Η τιμή του είναι μια
χαρακτηριστική για τα δύο μέταλλα συνάρτηση της θερμοκρασίας.
Ι = ένταση του ρεύματος,
t = χρόνος.
Εφαρμογές: Ψύξη μικρών αντικειμένων (π.χ. ολοκληρωμένων
κυκλωμάτων!).
Το μαγνητικό
πεδίο αποτελεί την δεύτερη μορφή εμφάνισης του ηλεκτρομαγνητικού πεδίου.
Η δημιουργία του
μαγνητικού πεδίου είναι αποτέλεσμα της κίνησης
ηλεκτρικών φορτίων, ενώ το ηλεκτρικό απλώς της παρουσίας τους.
Στην περίπτωση
των μονίμων μαγνητών ή γενικότερα μαγνητισμένων σωμάτων τα ρεύματα, τα οποία
δημιουργούν το πεδίο, είναι αποτέλεσμα της κίνησης των ηλεκτρονίων γύρω από
τους θετικά φορτισμένους πυρήνες.
4.1 Ένταση του μαγνητικού πεδίου. Δύναμη Lorentz
Η δύναμη, η
οποία ασκείται σε κινούμενο φορτίο q, το οποίο βρίσκεται εντός μαγνητικού πεδίου, καλείται δύναμη
Lorentz (στην ελληνική
βιβλιογραφία συνήθως δύναμη
![]() ®
® ![]() [
4.1]
[
4.1]
όπου ![]() = δύναμη Lorentz (
= δύναμη Lorentz (
![]() = ταχύτητα του φορτίου q
= ταχύτητα του φορτίου q
![]() = ένταση
του μαγνητικού πεδίου (παλαιότερα
μαγνητική επαγωγή)
= ένταση
του μαγνητικού πεδίου (παλαιότερα
μαγνητική επαγωγή)
Από την σχέση
[4.1]. προκύπτει:
α) Η δύναμη Lorentz είναι κάθετη και προς την
ταχύτητα του φορτίου και προς την ένταση του πεδίου.
β) Όταν το φορτίο κινείται παράλληλα προς
το μαγνητικό πεδίο δεν ασκείται δύναμη Lorentz επ’ αυτού. (αν ![]() )
)
γ) Η δύναμη Lorentz γίνεται μέγιστη (![]() ), όταν το φορτίο κινείται κάθετα προς την διεύθυνση του
μαγνητικού πεδίου.
), όταν το φορτίο κινείται κάθετα προς την διεύθυνση του
μαγνητικού πεδίου.
Η φορά
της δύναμης Lorentz προκύπτει άμεσα από τον ορισμό του διανυσματικού
γινομένου: αν τοποθετήσουμε δεξιόστροφο κοχλία κάθετα στο επίπεδο των
διανυσμάτων ![]() και
και ![]() και τον στρέψουμε
από το πρώτο προς το δεύτερο, τότε ο κοχλίας θα προχωρήσει κατά την φορά της
και τον στρέψουμε
από το πρώτο προς το δεύτερο, τότε ο κοχλίας θα προχωρήσει κατά την φορά της ![]() , εφόσον το φορτίο q είναι θετικό, διαφορετικά κατά την
αντίθετη.
, εφόσον το φορτίο q είναι θετικό, διαφορετικά κατά την
αντίθετη.
Η μονάδα της
μαγνητικής έντασης στο σύστημα SI καλείται Τ(esla).
Όταν ένα φορτίο q κινείται
συγχρόνως μέσα σε χώρο ηλεκτρικού πεδίου
εντάσεως ![]() και μαγνητικού
πεδίου εντάσεως
και μαγνητικού
πεδίου εντάσεως ![]() , δέχεται την επίδραση συνισταμένης δύναμης
, δέχεται την επίδραση συνισταμένης δύναμης
![]() [4.2]
[4.2]
4.2 Οι μαγνητικές δυναμικές γραμμές και η ροή τους
Οι μαγνητικές δυναμικές γραμμές δεν έχουν αρχή και τέλος: είναι κλειστές.
Ακόμη και στην
περίπτωση των μονίμων μαγνητών, τα άκρα των οποίων χαρακτηρίζονται από μια
πύκνωση των μαγνητικών δυναμικών γραμμών και ονομάζονται πόλοι, δεν έχουμε κάτι
αντίστοιχο προς τα ηλεκτρικά φορτία. Άλλωστε οι πόλοι εμφανίζονται πάντα κατά
ζεύγη:
δεν υπάρχουν «μαγνητικά φορτία»
αλλά μαγνητικά δίπολα.
Οι πόλοι ενός
μαγνήτη χαρακτηρίζονται αυθαίρετα σαν βόρειος και νότιος.
Η μαγνητική
ροή Φ μέσω μιας προσανατολισμένης επιφάνειας ![]() ορίζεται σε πλήρη
αντιστοιχία προς την ηλεκτρική ροή (βλ. §1.5):
ορίζεται σε πλήρη
αντιστοιχία προς την ηλεκτρική ροή (βλ. §1.5):
![]() [4.3]
[4.3]
Μονάδα μέτρησης
της μαγνητικής ροής στο SI είναι το Weber: ![]()
Λόγω της
ανυπαρξίας μαγνητικών μονοπόλων μηδενίζεται η συνολική μαγνητική ροή μέσω
οιασδήποτε κλειστής επιφάνειας:
![]() [4.4]
[4.4]
Η παραπάνω σχέση είναι μια από τις
τέσσερις θεμελιώδεις εξισώσεις του Maxwell. Αντικατοπτρίζει
δε την ανυπαρξία μαγνητικών φορτίων (μονοπόλων).
Παραδείγματα μαγνητικών γραμμών:
Σχήμα 4.1: Μαγνητικές δυναμικές γραμμές α) ενός
ευθυγράμμου, ρευματοφόρου αγωγού, β) ενός κυκλικού αγωγού και γ) ενός σωληνοειδούς.
4.3 Δύναμη μαγνητικού πεδίου επί ρευματοφόρου αγωγού
|
Σχήμα 4.2: Δύναμη επί ρευματοφόρου αγωγού, ο οποίος
βρίσκεται εντός μαγνητικού πεδίου. |
Όταν
ένας ρευματοφόρος αγωγός βρεθεί εντός μαγνητικού πεδίου, δέχεται την επίδραση
μαγνητικής δύναμης, η οποία είναι η συνισταμένη όλων των δυνάμεων Lorentz, οι οποίες
ασκούνται επί των κινουμένων φορτίων. Για την περίπτωση ενός ευθυγράμμου
αγωγού μήκους l, ο οποίος διαρρέεται από συνεχές ρεύμα έντασης Ι
και βρίσκεται εντός ομογενούς μαγνητικού πεδίου έντασης ![]() προκύπτει:
προκύπτει:
![]() [4.5]
[4.5]
(Η
Διεύθυνση του διανύσματος![]() συμπίπτει με
εκείνη του άξονα του αγωγού, ενώ η φορά του με την συμβατική φορά του ρεύματος).
συμπίπτει με
εκείνη του άξονα του αγωγού, ενώ η φορά του με την συμβατική φορά του ρεύματος).
4.4 Υπολογισμός της έντασης του μαγνητικού πεδίου ρευματοφόρων αγωγών
4.4.1 Ο νόμος του Ampere και οι εφαρμογές του
Η σχέση μεταξύ
του ρεύματος, το οποίο διαρρέει έναν ρευματοφόρο αγωγό, και της έντασης του
γύρω από τον αγωγό δημιουργούμενου μαγνητικού πεδίου δίδεται από τον ακόλουθο
«νόμο του Ampere»:
νόμος του Ampere: ![]() [4.6]
[4.6]
όπου μ0 = μαγνητική διαπερατότητα του κενού = 4π10-7 WbA-1m-1
iολ είναι το συνολικό ρεύμα,
το οποίο περικλείεται από την τυχαία κλειστή διαδρομή L. Συγκεκριμένα στην περίπτωση που η διαδρομή
περικλείει περισσότερα του ενός ρεύματα, το Iολ ισούται με το
αλγεβρικό τους άθροισμα, το οποίο υπολογίζεται θεωρώντας θετικά τα ρεύματα
εκείνα, των οποίων το μαγνητικό πεδίο έχει την ίδια φορά, με την φορά κατά την
οποία διατρέχουμε την κλειστή καμπύλη L. Ένα απλό παράδειγμα δείχνει το σχήμα 4.3.
|
|
Σχήμα 4.3: Παράδειγμα υπολογισμού
του ολικού ρεύματος iολ στον νόμο του Ampere. |
Εφαρμογές:
α) Υπολογισμός
της έντασης του μαγνητικού πεδίου (ιδανικού) σωληνοειδούς: Σαν σωληνοειδές
ορίζεται κάθε σπειροειδώς διαμορφωμένος αγωγός, του οποίου οι ισαπέχουσες σπείρες έχουν κοινό άξονα και ίδια ακτίνα.
|
Σχήμα 4.5: Για τον υπολογισμό του μαγνητικού πεδίου
ιδανικού σωληνοειδούς. |
Στην περίπτωση
ενός ιδανικού
σωληνοειδούς η ένταση του πεδίου
στο εξωτερικό του σωληνοειδούς είναι αμελητέα , ενώ στο εσωτερικό του επικρατεί
ένα ομογενές και παράλληλο προς τον άξονα του σωληνοειδούς μαγνητικό πεδίο (βλ.
σχ.4.5).
Ο νόμος του Ampere για την
διαδρομή ![]() του σχήματος 4.5
μας δίνει:
του σχήματος 4.5
μας δίνει:
![]() [4.7]
[4.7]
Η παραπάνω σχέση
αντικατοπτρίζει το γεγονός, ότι το μαγνητικό πεδίο ιδανικού σωληνοειδούς στον
εντός των σπειρών ευρισκόμενο χώρο είναι ομογενές και μάλιστα ανεξάρτητο από την διάμετρο των σπειρών.
|
Σχήμα 4.6: «Κάτοψη» μαγνητικού πεδίου ευθυγράμμου,
ρευματοφόρου αγωγού απείρου μήκους. |
β) Υπολογισμός
της έντασης του μαγνητικού πεδίου ευθυγράμμου, ρευματοφόρου αγωγού, πολύ μεγάλου
(απείρου) μήκους:
Εφαρμόζουμε τον
νόμο του Ampere επιλέγοντας ως
κλειστή διαδρομή L μια δυναμική γραμμή ακτίνας r, οπότε έχουμε:
![]() [4.8]
[4.8]
Σε περιπτώσεις τυχαίας κατανομής ρεύματος ο υπολογισμός της έντασης ![]() μπορεί να γίνει με την βοήθεια του νόμου των Biot - Savart, ο οποίος διατυπώνεται ως εξής:
μπορεί να γίνει με την βοήθεια του νόμου των Biot - Savart, ο οποίος διατυπώνεται ως εξής:
|
Σχήμα 4.7: Για τον νόμο των Biot-Savart. |
νόμος των Biot - Savart:
![]() [4.9]
[4.9]
Η ολική ένταση ![]() στο σημείο P υπολογίζεται με
ολοκλήρωση
στο σημείο P υπολογίζεται με
ολοκλήρωση ![]() , η οποία εκτείνεται σε όλη την κατανομή ρεύματος.
, η οποία εκτείνεται σε όλη την κατανομή ρεύματος.
|
Σχήμα 4.8: Για τον υπολογισμό του μαγνητικού πεδίου στο
κέντρο κυκλικού αγωγού. |
Παράδειγμα: Υπολογισμός
της έντασης του μαγνητικού πεδίου στο κέντρο κυκλικού αγωγού ακτίνας r (βλ. σχ. 4.8.):
Biot - Savart: ![]()
![]() [4.10]
[4.10]
(Η φορά του πεδίου προκύπτει κατά τα γνωστά με
την βοήθεια του εμπειρικού κανόνα των δακτύλων του δεξιού χεριού, βλ. §4.4.1).
4.5 Περιπτώσεις δυνάμεων ασκουμένων από μαγνητικά πεδία. Εφαρμογές
α) Δυνάμεις μεταξύ παραλλήλων ρευματοφόρων
αγωγών πολύ μεγάλου μήκους.
|
Σχήμα 4.9 |
:![]() [4.11]
[4.11]
Η παραπάνω σχέση χρησιμοποιείται για τον ορισμό του Ampere, μιας εκ των θεμελιωδών μονάδων του Διεθνούς Συστήματος.
β) Ροπή
επί ρευματοφόρου πλαισίου εντός ομογενούς μαγνητικού πεδίου:
![]() ή
διανυσματικά
ή
διανυσματικά ![]() [4.12]
[4.12]
όπου ![]() είναι το γνωστό
μας «επιφανειακό διάνυσμα», κάθετο επί του πλαισίου και με φορά προσδιοριζόμενη
από εκείνη του ρεύματος με την βοήθεια δεξιόστροφου κοχλία.
είναι το γνωστό
μας «επιφανειακό διάνυσμα», κάθετο επί του πλαισίου και με φορά προσδιοριζόμενη
από εκείνη του ρεύματος με την βοήθεια δεξιόστροφου κοχλία.
Η μηχανική ροπή ![]() μηδενίζεται, όταν το διάνυσμα
μηδενίζεται, όταν το διάνυσμα ![]() γίνει παράλληλο, άρα το πλαίσιο κάθετο προς το
πεδίο.
γίνει παράλληλο, άρα το πλαίσιο κάθετο προς το
πεδίο.
Το φαινόμενο της δράσης μηχανικής ροπής επί
ρευματοφόρου πλαισίου εντός μαγνητικού πεδίου βρίσκει εφαρμογή σε πολλά όργανα μέτρησης, όπως αμπερόμετρα και
βολτόμετρα. Επιπλέον αποτελεί την αρχή λειτουργίας των
ηλεκτροκινητήρων.
|
Σχήμα 4.11: Φαινόμενο Hall. |
γ) Φαινόμενο
Hall καλείται η εμφάνιση
ηλεκτρικής τάσεως ![]() , (τάση Hall) κάθετα προς την
διεύθυνση της ροής του ρεύματος εντός μεταλλικής ταινίας, όταν αυτή βρίσκεται
μέσα σε μαγνητικό πεδίο (βλ. σχ. 4.11). Η εν λόγω τάση αναπτύσσεται εξ αιτίας
του διαχωρισμού των φορέων φορτίου, ο οποίος είναι αποτέλεσμα της μετακίνησης
των ελευθέρων ηλεκτρονίων κάτω από την επίδραση της δύναμης Lorentz - προς την μια
πλευρά του αγωγού, οπότε προκαλείται περίσσεια θετικών ιόντων στην απέναντι.
, (τάση Hall) κάθετα προς την
διεύθυνση της ροής του ρεύματος εντός μεταλλικής ταινίας, όταν αυτή βρίσκεται
μέσα σε μαγνητικό πεδίο (βλ. σχ. 4.11). Η εν λόγω τάση αναπτύσσεται εξ αιτίας
του διαχωρισμού των φορέων φορτίου, ο οποίος είναι αποτέλεσμα της μετακίνησης
των ελευθέρων ηλεκτρονίων κάτω από την επίδραση της δύναμης Lorentz - προς την μια
πλευρά του αγωγού, οπότε προκαλείται περίσσεια θετικών ιόντων στην απέναντι.
![]() [4.14]
[4.14]
όπου ![]() :σταθερά Hall
:σταθερά Hall
Το φαινόμενο Hall βρίσκει
συνεχώς εφαρμογή στην μέτρηση της έντασης των μαγνητικών πεδίων.
Ως ηλεκτρομαγνητική
επαγωγή χαρακτηρίζεται το φαινόμενο της εμφάνισης ΗΕΔ στα άκρα ενός αγωγού
σαν συνέπεια της μεταβολής της μαγνητικής ροής μέσω της επιφάνειας, η οποία
περιορίζεται, από τον αγωγό γεωγραφικά ή/και χρονικά.
Την τιμή της
παραπάνω, επαγωγικής καλούμενης ηλεκτρεγερτικής δύναμης Εεπ
δίνει ο παρακάτω
Νόμος της ηλεκτρομαγνητικής
επαγωγής του Faraday
Η επαγωγική ΗΕΔ Εεπ , η οποία αναπτύσσεται στα άκρα ενός
αγωγού, ισούται (κατ’ απόλυτη τιμή) με τον ρυθμό μεταβολής της μαγνητικής ροής
Φ μέσω της επιφάνειας, την οποία περιορίζει ο αγωγός γεωγραφικά ή/και χρονικά:
![]() [4.14]
[4.14]
Παρατήρηση: α) Το αρνητικό πρόσημο
ερμηνεύεται από τον λεγόμενο κανόνα
του Lenz, ο οποίος αποτελεί συνέπεια της διατήρησης
της ενέργειας, και σύμφωνα με τον οποίο
η επαγωγική ΗΕΔ έχει τέτοια φορά, ώστε τα επαγωγικά ρεύματα,
τα οποία τείνει να προκαλέσει (ή και προκαλεί στην περίπτωση κλειστού αγωγού),
να προσπαθούν (μέσω του δικού τους μαγνητικού πεδίου) να αναιρέσουν την αυτά
προκαλέσασα μεταβολή της μαγνητικής ροής.
Παραδείγματα:
γ1) Ευθύγραμμος
αγωγός κινούμενος με σταθερή ταχύτητα ν εντός ομογενούς μαγνητικού πεδίου
έντασης Β και κάθετα προς τις μαγνητικές γραμμές:
|
Σχήμα 4.15: Ευθύγραμμος αγωγός κινούμενος εντός μαγνητικού
πεδίου. |
Þ ![]() [4.15]
[4.15]
γ2) Επίπεδο πλαίσιο,
περιστρεφόμενο με σταθερή γωνιακή ταχύτητα ω εντός ομογενούς μαγνητικού πεδίου
έντασης Β, γύρω από τον κάθετο προς τις μαγνητικές δυναμικές γραμμές άξονα του
(βλ. σχ. 4.18): (Η εν λόγω διάταξη αποτελεί ουσιαστικά την αρχή
λειτουργίας της γεννήτριας εναλλασσόμενου ρεύματος).
![]() [4.16]
[4.16]
Σχήμα
4.18: Επίπεδο πλάισιο περιστρεφόμενο με σταθερή γωνιακή ταχύτητα εντός ομογενούς
μαγνητικού πεδίου.
γ3)
Χρονικώς μεταβαλλόμενα μαγνητικά πεδία: Η επαγωγική ΗΕΔ
εμφανίζεται σαν συνέπεια της μεταβολής της μαγνητικής ροής, άσχετα με το αίτιο
που την προκαλεί.
Ενώ τώρα στην
περίπτωση που η μαγνητική ροή μεταβάλλεται εξ αιτίας της σχετικής κίνησης
αγωγών και μαγνητών, η επαγόμενη ΗΕΔ μπορεί να ερμηνευτεί ως το μακροσκοπικό
αποτέλεσμα της δράσης της δυνάμεως Lorentz επί των ελευθέρων ηλεκτρονίων, η
εμφάνιση
Γύρω από κάθε χρονικά μεταβαλλόμενο μαγνητικό πεδίο επάγεται ένα ηλεκτρικό
πεδίο.
Το επαγόμενο
αυτό ηλεκτρικό πεδίο διαφέρει σημαντικά από τα γνωστά μας ηλεκτροστατικά
πεδία. Η γενεσιουργός του αιτία δεν είναι κάποια φορτία αλλά κάποιο
μεταβαλλόμενο μαγνητικό πεδίο. Εξ αιτίας της ιδιαιτερότητας αυτής τα επαγόμενα ηλεκτρικά πεδία είναι πεδία μη
συντηρητικά και έχουν κλειστές δυναμικές γραμμές,
4.6.1 Ο νόμος της ηλεκτρομαγνητικής επαγωγής ως μία από τις εξισώσεις του Maxwell
Στην γενική
περίπτωση κατά την οποία έχουμε και χρονικώς μεταβαλλόμενο μαγνητικό
πεδίο και κινούμενο βρόγχοπαίρνουμε:
![]() [4.17]
[4.17]
Η σχέση αυτή
είναι μια από τις θεμελιώδεις εξισώσεις του Ηλεκτρομαγνητισμού: η δεύτερη από τις εξισώσεις του Maxwell. Σημειωτέον ότι ![]() είναι η ένταση του
επαγόμενου ηλεκτρικού πεδίου για έναν με την ταχύτητα
είναι η ένταση του
επαγόμενου ηλεκτρικού πεδίου για έναν με την ταχύτητα ![]() ως προς το μαγνητικό
πεδίο
ως προς το μαγνητικό
πεδίο ![]() κινούμενο παρατηρητή.
κινούμενο παρατηρητή.
Το φαινόμενο της
ηλεκτρομαγνητικής επαγωγής βρίσκει ευρύτατες εφαρμογές στην τεχνολογία, οι
σπουδαιότερες από τις οποίες περιγράφονται εν συντομία στην συνέχεια.
α) Δινορρεύματα: Τα μέσω
ηλεκτρομαγνητικής επαγωγής στο εσωτερικό συμπαγών αγωγών εμφανιζόμενα ρεύματα,
καλούνται ρεύματα Foucault ή δινορρεύματα, το τελευταίο
επειδή συχνά είναι κυκλικά. Η φορά τους προσδιορίζεται από τον κανόνα του Lenz.
β) Δυναμικά μικρόφωνα:
Χρησιμοποιούνται για την μετατροπή ηχητικών ταλαντώσεων (ήχων) σε ηλεκτρικές.
γ) Ηλεκτρομαγνητικοί μεταποιητές:
Χρησιμοποιούνται για την μετατροπή μηχανικών μεγεθών, (π.χ. δυνάμεων, ταχυτήτων,
επιταχύνσεων) σε ηλεκτρικές τάσεις.
δ) Μαγνητοϋδροδυναμικά φαινόμενα: Το φαινόμενο
της ηλεκτρομαγνητικής επαγωγής εμφανίζεται φυσικά και στην περίπτωση ρευστών
αγωγών, δηλαδή στην περίπτωση αγώγιμων υγρών και αερίων, και επηρεάζει
σημαντικά τα χαρακτηριστικά ροής και τις επιμέρους ιδιότητές τους.
|
Σχήμα 4.21: Αρχή λειτουργίας της μαγνητοϋδροδυναμικής
γεννήτριας σχηματικά |
Στο φαινόμενο
της ηλεκτρομαγνητικής επαγωγής στην περίπτωση ταχέως κινουμένου πλάσματος στηρίζεται
η λειτουργία της λεγόμενης μαγνητοϋδροδυναμικής
(ΜΗD) γεννήτριας ηλεκτρικής
ενέργειας.
ε) Γεννήτριες εναλλασσόμενου και συνεχούς
ρεύματος:
Σχήμα 4.22: Αρχή παραγωγής εναλλασσόμενης τάσης – αρχή
λειτουργίας γεννήτριας εναλλασσομένου ρεύματος.
ζ) Ηλεκτροκινητήρες: Η λειτουργία
τους στηρίζεται στην αντιστροφή της αρχής λειτουργίας των γεννητριών
εναλλασσομένου και συνεχούς ρεύματος.
|
Σχήμα 4.25: σχηματική παράσταση μετασχηματιστή. |
η) Μετασχηματιστές: Ένας
μετασχηματιστής αποτελείται από δύο σωληνοειδή με διαφορετικό αριθμό σπειρών, τα
οποία είναι μαγνητικά συζευγμένα μέσω κλειστού πυρήνα (βλ. σχ. 4.25) από μαγνητικά
μαλακό σιδηρομαγνητικό υλικό.
Οι μετασχηματιστές χρησιμοποιούνται για τον μετασχηματισμό εναλλασσομένων
τάσεων ή και ηλεκτρικών παλμών.
Για έναν
ιδανικό μετασχηματιστή παίρνουμε:
![]() [4.19]
[4.19]
u1, είναι η τάση με
την οποία τροφοδοτείται το πρωτεύον σωληνοειδές και u2 η τάση η οποία
αναπτύσσεται στα άκρα του δευτερεύοντος σωληνοειδούς εξ αιτίας του φαινομένου
της αμοιβαίας επαγωγής.
Ο λόγος Ν1
/ Ν2 του αριθμού των σπειρών του πρωτεύοντος προς του
αριθμού των σπειρών του δευτερεύοντος σωληνοειδούς καλείται λόγος
μετασχηματισμού.
Στην περίπτωση ενός πραγματικού μετασχηματιστή δεν ισχύει η
ισότητα της ισχύος του πρωτεύοντος κυκλώματος με εκείνη του δευτερεύοντος, για τους ακόλουθους
κυρίως λόγους:
1)
Η μαγνητική ροή του δευτερεύοντος σωληνοειδούς είναι
ασθενέστερη λόγω μαγνητικής σκέδασης.
2)
Η ωμική αντίσταση των δύο σωληνοειδών δεν είναι αμελητέα,
γεγονός το οποίο συνεπάγεται την μετατροπή μέρος της ηλεκτρικής σε θερμική
ισχύ, μέσω του γνωστού μας φαινομένου Joule.
3)
Απώλειες ισχύος έχουμε επίσης λόγω φαινομένων μαγνητικής
υστέρησης στον πυρήνα του μαλακού σιδήρου, στον οποίο αναπτύσσονται και
δινορρεύματα παρά την φυλλωτή του κατασκευή, η οποία βέβαια τα περιορίζει
σημαντικά, όταν η συχνότητα της εναλλασσόμενης τάσης δεν ξεπερνά τα 50kHz.
Αυτεπαγωγή καλείται το
φαινόμενο της εμφάνισης ΗΕΔ εξ επαγωγής στα άκρα ενός αγωγού εξ αιτίας
της μεταβολής του ρεύματος (άρα και του αντιστοίχου μαγνητικού πεδίου) που τον
διαρρέει.
Το φαινόμενο της
αυτεπαγωγής είναι ιδιαίτερα έντονο στην περίπτωση ενός σωληνοειδούς, εξ αιτίας
της μεγάλης εντάσεως του μαγνητικού του πεδίου καθώς και της μεγάλης επιφάνειας
(= συνολική επιφάνεια όλων των σπειρών του σωληνοειδούς), η οποία διαρρέεται
απ’ αυτό. 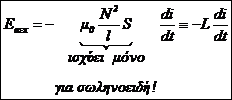 [4.21]
[4.21]
Η σταθερά αναλογίας L καλείται συντελεστής
αυτεπαγωγής (ή απλώς αυτεπαγωγή) του αγωγού και εξαρτάται από την γεωμετρία του αγωγού και από το
υλικό που περιβάλλεται, απ’ αυτόν. Στο Διεθνές Σύστημα μονάδων S.I. μονάδα μέτρησης
του L είναι το Vs/A και καλείται
Η(enry).
4.6.4 Επίδραση αυτεπαγωγής στο ρεύμα κυκλώματος LR
|
Σχήμα 4.27: Κύκλωμα RL. |
Όταν ο διακόπτης
δ μετακινηθεί προς την θέση α,
προκύπτει από τον 2° κανόνα του Kirchhoff:
![]() [4.22]
[4.22]
|
Σχήμα 4.28: Μεταβολή του ρεύματος I σε κύκλωμα RL. (a: διακόπτης
στην θέση α, b: διακόπτης στην θέση β) |
Αν ο διακόπτης
μετακινηθεί προς την θέση β προκύπτει από τον 2° κανόνα του Kirchhoff:
![]() [4.22]
[4.22]
Ο χρόνος t = L/R είναι η
χαρακτηριστική σταθερή χρόνου του
κυκλώματος.
Δύο αγωγοί, οι
οποίοι ευρίσκονται ο ένας τόσο πλησίον του άλλου, ώστε να «αλληλοαισθάνονται»
τις ενδεχόμενες μεταβολές των μαγνητικών τους πεδίων, χαρακτηρίζονται ως μαγνητικά
συζευγμένοι:
![]() [4.23]
[4.23]
Ο συντελεστής Λ καλείται συντελεστής
αμοιβαίας επαγωγής και εξαρτάται από την γεωμετρία (σχήμα και
διαστάσεις) των συζευγμένων αγωγών, την σχετική τους θέση καθώς και τις
μαγνητικές ιδιότητες του περιβάλλοντος μέσου. Όπως δε και ο συντελεστής αυτεπαγωγής
μετράται σε Henry.
4.7 Ενέργεια και πυκνότητα ενέργειας μαγνητικού πεδίου
Η ενέργεια του μαγνητικού πεδίου ενός
σωληνοειδούς, συντελεστή L, το οποίο διαρρέεται
από ρεύμα έντασης i, δίδεται από την σχέση:
![]() [4.24]
[4.24]
Η ενέργεια αυτή
επαναδιοχετεύεται στο κύκλωμα κατά την αποσύνδεση του μαγνητικού πεδίου, η
οποία επέρχεται όταν αποσυνδέσουμε το σωληνοειδές από την πηγή.
Για την πυκνότητα
ενέργειας προκύπτει:
πυκνότητα ενέργειας μαγνητικού πεδίου: 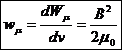 [4.25]
[4.25]
Εναλλασσόμενο καλείται το ρεύμα, του οποίου η τιμή και η φορά
είναι περιοδικές συναρτήσεις του χρόνου. Στην περίπτωση δε που πρόκειται για ημιτονοειδή
(ή συνιμητονοειδή) συνάρτηση, το εναλλασσόμενο ρεύμα χαρακτηρίζεται ως
αρμονικό. Αυτή την ειδική κατηγορία εναλλασσομένου ρεύματος θα
εννοούμε, ακόμη και όταν μιλάμε απλώς για εναλλασσόμενο ρεύμα, εκτός και αν το
τονίζουμε, ότι πρόκειται για μη ημιτονοειδές εναλλασσόμενο ρεύμα.
Ένα κύκλωμα
διαρρέεται από εναλλασσόμενο ρεύμα, όταν στα άκρα του εφαρμόζεται εναλλασσόμενη
τάση: τάση της οποίας η τιμή και το πρόσημο είναι περιοδικές συναρτήσει
του χρόνου.
Η γενική
εξίσωση ενός (αρμονικώς) εναλλασσομένου μεγέθους α έχει την μορφή
![]() [5.1]
[5.1]
όπου Α0 = πλάτος
του εναλλασσομένου μεγέθους.
ω = κυκλική
συχνότητα του εναλλ. μεγέθους. (Στην περίπτωση π.χ. που το
εναλλασσόμενο μέγεθος είναι η στα άκρα εντός μαγνητικού πεδίου περιστρεφόμενου
πλαισίου αναπτυσσόμενη τάση, η κυκλική συχνότητα ισούται αριθμητικά με την
γωνιακή ταχύτητα του πλαισίου. Βέβαια η φυσική υπόσταση της κυκλικής συχνότητας
είναι εντελώς διαφορετική από εκείνη της γωνιακής ταχύτητας!)
t = ο χρόνος
(ωt + φ) = φάση του εναλλ. μεγέθους.
Σημειωτέον ότι η φάση μετράται σε ακτίνια (rad)!
φ = αρχική φάση του εναλλ. μεγέθους, δηλ. φάση
κατά την χρονική στιγμή t = 0. (Στην περίπτωση της εναλλασσόμενης τάσης
περιστρεφόμενου πλαισίου, η μεν φάση (ωt + φ) ισούται με την γωνία μεταξύ της
καθέτου επί του πλαισίου και της διεύθυνσης του πεδίου σε μια τυχαία χρονική
στιγμή t, η δε αρχική
φάση με την τιμή της εν λόγω γωνίας κατά την χρονική στιγμή t = 0).
Χρησιμοποιώντας
τις γνωστές σχέσεις ![]() [5.2],
[5.2],
παίρνουμε τις
ακόλουθες, ισοδύναμες προς την [5.1] σχέσεις:
|
Σχήμα 5.1: Χρονοδιάγραμμα αρμονικού εναλλ. μεγέθους
με αρχική φάση ίση με μηδέν. |
![]() [5.1α]
[5.1α]
όπου ν = συχνότητα εναλλ.
μεγέθους. Ισούται με τον αριθμό των πλήρων εναλλαγών του εναλλασσομένου
μεγέθους στην μονάδα του χρόνου. (Στην περίπτωση της εναλλασσόμενης τάσης, η
οποία παράγεται μέσω περιστρεφόμενου πλαισίου, ισούται ουσιαστικά με τον αριθμό
περιστροφών του πλαισίου στην μονάδα του χρόνου).
Τ = περίοδος του εναλλ.
μεγέθους. Πρόκειται για τον χρόνο μεταξύ δύο πλήρων διαδοχικών εναλλαγών, εντός
του οποίου το εναλλασσόμενο μέγεθος ολοκληρώνει όλο το φάσμα των τιμών του,
οπότε επαναλαμβάνεται ο ίδιος κύκλος τιμών. (Στην περίπτωση της γνωστής μας
πλέον εναλλασσόμενης τάσης η περίοδος ισούται αριθμητικά με τον χρόνο μιας
πλήρους περιστροφής του πλαισίου).
Τα παραπάνω
χαρακτηριστικά γίνονται κατανοητά με την βοήθεια του διπλανού χρονοδιαγράμματος,
στο οποίο απεικονίζεται ένα τυχαίο εναλλασσόμενο μέγεθος, του οποίου η αρχική
φάση ισούται με μηδέν.
5.2 Παράσταση εναλλασσομένου μεγέθους μέσω περιστρεφομένου ανύσματος
Στις
περισσότερες εφαρμογές, η στιγμιαία τιμή ενός εναλλασσομένου μεγέθους έχει
μικρή έως και ανεπαίσθητη αξία. Για τους λόγους αυτούς στην πράξη προτιμάται
συνήθως
Η γραφική παράσταση ενός εναλλασσομένου
μεγέθους με την βοήθεια περιστρεφομένου ανύσματος στηρίζεται στους
ακόλουθους συμβατικούς κανόνες:
α) Σ’ ένα
ορθοκανονικό σύστημα αξόνων xy παίρνουμε (βλ. σχ. 5.2) άνυσμα ![]() , του οποίου το μήκος θα ισούται αριθμητικά με το πλάτος
Α0 του εναλλασσομένου μεγέθους α.
, του οποίου το μήκος θα ισούται αριθμητικά με το πλάτος
Α0 του εναλλασσομένου μεγέθους α.
β) Το εν λόγω
άνυσμα τοποθετείται στο διάγραμμα έτσι ώστε η μεν αρχή του να συμπίπτει με την
αρχή των αξόνων, η δε διεύθυνση του σχηματίζει με τον οριζόντιο άξονα x γωνία y, ίση με την
αρχική φάση του εναλλασσομένου μεγέθους.
γ) Η στιγμιαία τιμή
του εναλλασσομένου μεγέθους κατά την τυχαία χρονική στιγμή t υπολογίζεται με
τον ακόλουθο τρόπο: θεωρούμε, ότι το άνυσμα ![]() περιστρέφεται με
σταθερή γωνιακή ταχύτητα ω, ίση προς την κυκλική συχνότητα του εναλλασσομένου
μεγέθους, και κατά την αντίθετη προς εκείνη των δεικτών του ωρολογίου φορά.
Τότε η προβολή του ανύσματος
περιστρέφεται με
σταθερή γωνιακή ταχύτητα ω, ίση προς την κυκλική συχνότητα του εναλλασσομένου
μεγέθους, και κατά την αντίθετη προς εκείνη των δεικτών του ωρολογίου φορά.
Τότε η προβολή του ανύσματος ![]() επί του άξονα y («άξονας
προβολών») ισούται αριθμητικά με την στιγμιαία τιμή
επί του άξονα y («άξονας
προβολών») ισούται αριθμητικά με την στιγμιαία τιμή ![]() του εναλλασσομένου
μεγέθους α. Εξάλλου η γωνία μεταξύ της διεύθυνσης του ανύσματος και του άξονα x («άξονας
φάσεων») ισούται με την φάση (
του εναλλασσομένου
μεγέθους α. Εξάλλου η γωνία μεταξύ της διεύθυνσης του ανύσματος και του άξονα x («άξονας
φάσεων») ισούται με την φάση (![]() ) κατά την τυχαία χρονική στιγμή t.
) κατά την τυχαία χρονική στιγμή t.
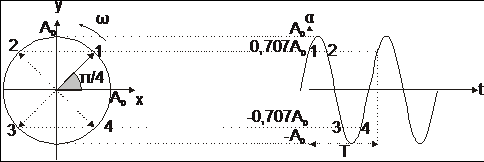
Σχήμα 5.2: Διανυσματική
παράσταση εναλλασσομένου μεγέθους α = Α0sin(ωt + φ) με την βοήθεια περιστρεφομένου ανύσματος. Η
αρχική φάση φ θεωρήθηκε ίση με π/4 (= 45ο).
|
Σχήμα 5.3: Διανυσματική παράσταση δύο εναλλασσομένων μεγεθών
με πλάτη Α01 και Α02, κυκλική συχνότητα ω και αρχικές φάσεις φ1 = π/4 και φ2=
-π/2 αντίστοιχα. |
Η γραφική
παράσταση ενός εναλλασσομένου μεγέθους μέσω περιστρεφόμενου ανύσματος αποδίδει
άμεσα όλα τα ενδιαφέροντα στοιχεία του
εναλλασσομένου μεγέθους: πλάτος, αρχική φάση, διαφορά φάσεως μεταξύ δύο ή
περισσοτέρων μεγεθών, καθώς και την κυκλική συχνότητα ω του απεικονιζόμενου μεγέθους,
η οποία συμβολίζεται με ένα βέλος ως γωνιακή ταχύτητα του
περιστρεφόμενου ανύσματος. Στο σχήμα 5.3 για παράδειγμα απεικονίζονται μέσω
διανυσμάτων δύο εναλλασσόμενα μεγέθη με πλάτη Α01 και Α02,
κυκλική συχνότητα ω και αρχικές φάσεις φ1 = π/4 και φ2=
-π/2 αντίστοιχα. Από το σχήμα φαίνεται άμεσα, ότι η διαφορά φάσεως ισούται με
3π/4.
Δύσχρηστη
γίνεται η διανυσματική παράσταση εναλλασσομένων μεγεθών, όταν πρέπει να κάνουμε διαιρέσεις, παραγωγίσεις και
ολοκληρώσεις εναλλασσομένων μεγεθών. Προκειμένου να αντιμετωπίσουμε τις
εν λόγω υπολογιστικές δυσκολίες καταφεύγουμε στην
5.3 Μιγαδική παράσταση εναλλασσομένων μεγεθών
Ένας μιγαδικός
αριθμός ζ μπορεί
να γραφεί πάντα στην (ορθοκανονική
ή καρτεσιανή, όπως λέγεται) μορφή
![]() [5.3]
[5.3]
όπου x, y δύο τυχαίοι πραγματικοί αριθμοί.
Οι πραγματικοί
αριθμοί x και y χαρακτηρίζονται
ως το πραγματικό και φανταστικό μέρος του
μιγαδικού αριθμού ![]() αντίστοιχα, γεγονός το οποίο εκφράζεται
συμβολικά ως εξής:
αντίστοιχα, γεγονός το οποίο εκφράζεται
συμβολικά ως εξής:
![]()
![]() [5.3α]
[5.3α]
Το j εξάλλου
ονομάζεται φανταστική μονάδα και ορίζεται έτσι ώστε ![]() [ 5.4 ]
[ 5.4 ]
|
Σχήμα 5.4: Ορθοκανονονική και πολική γραφή ενός μιγαδικού
αριθμού. |
Οι μιγαδικοί
αριθμοί μπορούν να παρασταθούν γραφικά σαν σημεία σε ένα ορθοκανονικό σύστημα
αξόνων x, y. Ο οριζόντιος
άξονας x καλείται πραγματικός
άξονας, ενώ ο y φανταστικός
άξονας. (βλ. σχ. 5.4).
Συχνά
χρησιμοποιείται η πολική γραφή
ενός μιγαδικού αριθμού
![]() [5.5]
[5.5]
όπου ![]() = μέτρο του μιγαδικού αριθμού
= μέτρο του μιγαδικού αριθμού ![]()
φ = όρισμα του μιγαδικού
αριθμού ![]() : φ = Αrg(
: φ = Αrg(![]() )
)
Η γωνία φ μπορεί
να υπολογισθεί από την σχέση tanφ = y/x.
|
Σχήμα 5.5: Περιγραφή ενός ανύσματος |
Η σχέση
του Εuler:
![]() [5.6],
[5.6],
μας επιτρέπει να
γράψουμε έναν μιγαδικό αριθμό ![]() με την ακόλουθη
εκθετική μορφή:
με την ακόλουθη
εκθετική μορφή:
![]() [5.7]
[5.7]
Εύκολα
αποδεικνύεται ότι
![]() [ 5.8 ]
[ 5.8 ]
Εκθετική
μιγαδική παράσταση εναλλασσομένων μεγεθών:
Ένα εναλλασσόμενο μέγεθος ![]() μπορεί να θεωρηθεί, ότι παριστάνεται από το φανταστικό μέρος του μιγαδικού αριθμού
μπορεί να θεωρηθεί, ότι παριστάνεται από το φανταστικό μέρος του μιγαδικού αριθμού ![]() , αφού σύμφωνα με την σχέση του Euler έχουμε:
, αφού σύμφωνα με την σχέση του Euler έχουμε: ![]()
Στην παραπάνω
εκθετική μιγαδική παράσταση του εναλλασσομένου μεγέθους α διακρίνουμε άμεσα το
πλάτος του Α0, την κυκλική του συχνότητα ω, την φάση ωt + φ και την
αρχική του φάση φ.
Από τα παραπάνω
προκύπτει ο ακόλουθος κανόνας, ο οποίος μας επιτρέπει να γράψουμε απ'
ευθείας την τριγωνομετρική μορφή ενός εναλλασσομένου μεγέθους ![]() , το οποίο παριστάνεται συμβολικά μέσω
του φανταστικού μέρους του μιγαδικού αριθμού
, το οποίο παριστάνεται συμβολικά μέσω
του φανταστικού μέρους του μιγαδικού αριθμού ![]() :
:
Γράφουμε τον
μιγαδικό αριθμό στην συμβολική μορφή ![]() και στην συνέχεια αντικαθιστούμε το σύμβολο «∟» με το ημίτονο («sin»):
και στην συνέχεια αντικαθιστούμε το σύμβολο «∟» με το ημίτονο («sin»):
![]()
Κατά την μελέτη
κυκλωμάτων εναλλασσομένου ρεύματος ενδιαφερόμαστε κυρίως για το ρεύμα, το οποίο
διαρρέει το υπό μελέτη κύκλωμα, όταν στα άκρα του κυκλώματος εφαρμόζεται
εναλλασσόμενη τάση ![]() , πλάτους U0 και κυκλικής
συχνότητας ω. Όπως δε θα δούμε στο επόμενο κεφάλαιο, το ρεύμα είναι επίσης
εναλλασσόμενο, η δε στιγμιαία του τιμή δίδεται από την εξίσωση
, πλάτους U0 και κυκλικής
συχνότητας ω. Όπως δε θα δούμε στο επόμενο κεφάλαιο, το ρεύμα είναι επίσης
εναλλασσόμενο, η δε στιγμιαία του τιμή δίδεται από την εξίσωση ![]() , όπου το πλάτος Ι0
και η διαφορά φάσεως φ (ως προς την τάση) εξαρτώνται από την δομή του κυκλώματος.
Σύμφωνα τώρα με όσα αναπτύξαμε στις προηγούμενες παραγράφους, τάση και ρεύμα
μπορούν να γραφούν σε μιγαδική μορφή ως εξής:
, όπου το πλάτος Ι0
και η διαφορά φάσεως φ (ως προς την τάση) εξαρτώνται από την δομή του κυκλώματος.
Σύμφωνα τώρα με όσα αναπτύξαμε στις προηγούμενες παραγράφους, τάση και ρεύμα
μπορούν να γραφούν σε μιγαδική μορφή ως εξής:
![]()
![]()
[5.17]
![]()
![]()
Η συμπεριφορά της πραγματικής τάσεως και εντάσεως
αποδίδεται (συμβατικά) από το φανταστικό
(!) μέρος της μιγαδικής τάσεως και εντάσεως αντιστοίχως:
![]()
![]() [5.17α]
[5.17α]
5.4 Μελέτη κυκλώματος RLC (σε σειρά)
|
|
Στο κύκλωμα του
διπλανού σχήματος, το οποίο αποτελείται από ωμική αντίσταση τιμής R, σωληνοειδές αυτεπαγωγής
L και πυκνωτή
χωρητικότητας C συνδεμένα σε
σειρά, μεταβάλλεται εκτός από την στα άκρα του κυκλώματος ασκούμενη τάση u, όπως είναι φυσικό,
και η ένταση i του ρεύματος, η
οποία όμως σε μια δεδομένη χρονική στιγμή t είναι η ίδια σε όλο το μήκος του
κυκλώματος.
Οι στιγμιαίες
τιμές των τάσεων που παρατηρούνται στα στοιχεία του παραπάνω κυκλώματος
δίδονται από τις ακόλουθες, γνωστές μας σχέσεις:
![]() {1}
(Νόμος του Ohm)
{1}
(Νόμος του Ohm)
![]() {2} (Νόμος της ηλεκτρομαγνητικής
επαγωγής για την περίπτωση της αυτεπαγωγής)
{2} (Νόμος της ηλεκτρομαγνητικής
επαγωγής για την περίπτωση της αυτεπαγωγής)
![]() {3} (Ορισμός της
χωρητικότητας πυκνωτή)
{3} (Ορισμός της
χωρητικότητας πυκνωτή)
Σύμφωνα με τον
2° κανόνα του Kirchhoff θα ισχύει για
τις στιγμιαίες τιμές των τάσεων:
![]() {4}
{4}
→ ![]() {4α}
{4α}
Η επίλυση της
παραπάνω μη ομογενούς (ολοκληρω-) διαφορικής εξίσωσης μας δίνει ως αποτέλεσμα
το άθροισμα δύο ρευμάτων: ενός φθίνοντος εκθετικού και ενός αρμονικού. Το πρώτο
περιγράφει προφανώς την μεταβατική φάση της ενάρξεως της λειτουργίας του κυκλώματος
και είναι χωρίς ιδιαίτερο ενδιαφέρον, αφού αργά ή γρήγορα εξαφανίζεται.
Απομένει τότε το δεύτερο, αρμονικό ρεύμα, το οποίο περιγράφει την μόνιμη
κατάσταση, κατά την οποία το ρεύμα μεταβάλλεται με την συχνότητα που επιβάλλει
η στα άκρα του κυκλώματος εφαρμοζόμενη, αρμονική τάση, με πλάτος όμως
εξαρτώμενο αποφασιστικά από την τιμή των R, L και C.
Συγκεκριμένα η επίλυση της ομογενούς εξίσωσης {4 ή 4α} μας δίνει
ως αποτέλεσμα ένα ρεύμα, του οποίου η ένταση
φθίνει εκθετικά με τον χρόνο. Το ρεύμα
αυτό παρατηρείται επομένως μόνο κατά την έναρξη λειτουργίας του κυκλώματος και
είναι ως εκ τούτου περιορισμένου πρακτικού ενδιαφέροντος.
Η αρμονική τάση u με την σειρά
της περιμένουμε να προκαλεί ένα (επιπλέον) επίσης αρμονικό ρεύμα, της ίδιας
συχνότητας με αυτήν, αν και όχι αναγκαστικά και της ίδιας φάσης. Το αρμονικό
αυτό ρεύμα i θα αντιστοιχεί
προφανώς στην μερική λύση της μη ομογενούς εξίσωσης {4α}. Ο υπολογισμός του εν
λόγω αρμονικού ρεύματος απλουστεύεται δραματικά με την χρήση μιγαδικών αριθμών.
Μεταπηδούμε λοιπόν στον χώρο των μιγαδικών αριθμών, όπου η {4α} παίρνει την ακόλουθη
συμβολική μορφή:
![]() {5β}
{5β}
όπου ![]() και
και ![]()
![]()
![]()
Παίρνοντας υπόψη
τους κανόνες παραγώγισης και ολοκλήρωσης των μιγαδικών αριθμών, σύμφωνα με τους
οποίους η παραγώγιση/ολοκλήρωση ενός μιγαδικού αριθμού ως προς τον χρόνο
ισοδυναμεί με πολλαπλασιασμό του επί/διαίρεσή του δια (jω), έχουμε:
![]()
![]()
![]() [5.18]
[5.18]
|
όπου video11, video12,
video13, |
Η εξίσωση [5.18] χαρακτηρίζεται συνήθως
ως νόμος του Οhm για εναλλασσόμενα
ρεύματα. |
Το μέγεθος ![]() , το οποίο έχει προφανώς διαστάσεις αντίστασης, αφού ο
ένας προσθετέος είναι η ωμική αντίσταση R, χαρακτηρίζεται ως μιγαδική
σύνθετη αντίσταση του κυκλώματος.
, το οποίο έχει προφανώς διαστάσεις αντίστασης, αφού ο
ένας προσθετέος είναι η ωμική αντίσταση R, χαρακτηρίζεται ως μιγαδική
σύνθετη αντίσταση του κυκλώματος.
Ο νόμος λοιπόν του
Οhm για εναλλασσόμενα ρεύματα μπορεί να
διατυπωθεί ως εξής:
Η μιγαδική ένταση ![]() του ρεύματος, το
οποίο διαρρέει κύκλωμα (ή τμήμα κυκλώματος), στα άκρα του οποίου εφαρμόζεται η
αρμονική τάση u, υπολογίζεται διαιρώντας την μιγαδική
τάση
του ρεύματος, το
οποίο διαρρέει κύκλωμα (ή τμήμα κυκλώματος), στα άκρα του οποίου εφαρμόζεται η
αρμονική τάση u, υπολογίζεται διαιρώντας την μιγαδική
τάση ![]() με την μιγαδική σύνθετη αντίσταση
με την μιγαδική σύνθετη αντίσταση ![]() του κυκλώματος (ή του τμήματος κυκλώματος).
του κυκλώματος (ή του τμήματος κυκλώματος).
Πολύ συχνά η
μιγαδική σύνθετη αντίσταση ![]() γράφεται στην
ακόλουθη μορφή:
γράφεται στην
ακόλουθη μορφή: ![]() [5.18α]
[5.18α]
όπου R = ωμική
αντίσταση
RL = ωL = επαγωγική αντίσταση
![]() χωρητική αντίσταση
χωρητική αντίσταση
Αν εισάγουμε την
μιγαδική επαγωγική αντίσταση ![]() και την μιγαδική
χωρητική αντίσταση
και την μιγαδική
χωρητική αντίσταση ![]() , η σύνθετη
αντίσταση γράφεται:
, η σύνθετη
αντίσταση γράφεται: ![]()
Παρατηρούμε
λοιπόν, ότι οι μιγαδικές εναλλασσόμενες
αντιστάσεις όταν συνδέονται σε σειρά προστίθενται προκειμένου να διαμορφώσουν
την σύνθετη αντίσταση ![]() , συμπεριφέρονται δηλαδή όπως και
οι αντιστάσεις συνεχούς.
, συμπεριφέρονται δηλαδή όπως και
οι αντιστάσεις συνεχούς.
Ας ξαναγυρίσουμε
όμως στον υπολογισμό του ρεύματος ![]() . Προς τον σκοπό αυτό γράφουμε την μιγαδική σύνθετη
αντίσταση
. Προς τον σκοπό αυτό γράφουμε την μιγαδική σύνθετη
αντίσταση ![]() σε εκθετική μορφή:
σε εκθετική μορφή:
![]() {α}
{α}
![]() {β}
{β}
όπου 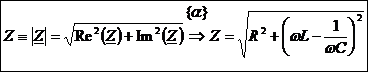 [5.20]
[5.20]
(απόλυτη τιμή ή
φαινομένη αντίσταση)
και 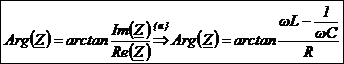 [5.20α]
[5.20α]
Από την [5.19]
παίρνουμε εξάλλου:
![]() [5.21]
[5.21]
με 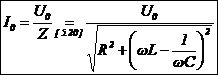 : πλάτος
εντάσεως video14 [5.21α]
: πλάτος
εντάσεως video14 [5.21α]
και 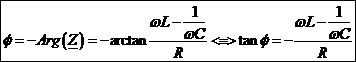 video15 [5.21β]
video15 [5.21β]
(διαφορά φάσεως μεταξύ τάσεως ![]() και εντάσεως
και εντάσεως ![]() )
)
ή
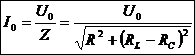 : πλάτος
εντάσεως [5.22]
: πλάτος
εντάσεως [5.22]
![]() [5.22α]
[5.22α]
(διαφορά φάσεως
μεταξύ τάσεως ![]() και εντάσεως
και εντάσεως ![]() )
)
με RL = ωL : επαγωγική αντίσταση
![]() : χωρητική αντίσταση
: χωρητική αντίσταση
5.4.1 Κανόνες του Kirchhoff για εναλλασσόμενα ρεύματα
1ος κανόνας του Kirchhoff για εναλλασσόμενα ρεύματα: Το άθροισμα των μιγαδικών εντάσεων των εναλλασσομένων
ρευμάτων ενός κόμβου ισούται με μηδέν.
2ος κανόνας του Kirchhoff για εναλλασσόμενα ρεύματα: Το άθροισμα των μιγαδικών εναλλασσομένων ΗΕΔ κατά μήκος
ενός βρόγχου ισούται με το άθροισμα των μιγαδικών πτώσεων τάσεως στις
μιγαδικές αντιστάσεις του βρόγχου.
Έστω τρεις
μιγαδικές σύνθετες αντιστάσεις ![]() ,
, ![]() και
και ![]() συνδεμένες
παράλληλα (βλ. σχ. 5.6).
συνδεμένες
παράλληλα (βλ. σχ. 5.6).
|
|
Από τον 1ο
κανόνα του Kirchhoff προκύπτει ότι:
![]()
![]()
Βλέπουμε λοιπόν,
ότι οι κανόνες υπολογισμού της ολικής σύνθετης μιγαδικής αντίστασης εναλλασσομένων
αντιστάσεων είναι και σ’ αυτήν την περίπτωση ίδιοι με εκείνους που ισχύουν και
για το συνεχές ρεύμα. Μπορούμε λοιπόν να συνοψίσουμε ως εξής:
Όταν δύο υπό εναλλασσομένου ρεύματος διαρρεόμενα
στοιχεία συνδέονται κατά σειρά, προστίθενται οι μιγαδικές τους
αντιστάσεις, όταν είναι συνδεμένα παράλληλα προστίθενται οι μιγαδικές
τους αγωγιμότητες.
Το πλάτος I0 και η διαφορά φάσεως φ μεταξύ τάσεως και
εντάσεως δίδονται, όπως είδαμε (βλ. [5.21] και [5.21α]), από τις σχέσεις:
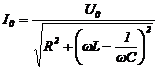
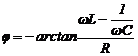 {1}
{1}
Εξαρτώνται
λοιπόν αμφότερα από την συχνότητα της εναλλασσόμενης τάσεως.
Η συμπεριφορά
του πλάτους Ι0 συναρτήσει της κυκλικής συχνότητας ω αποδίδεται
ποιοτικά στο σχήμα 5.6 για δύο διαφορετικές τιμές της ωμικής αντίστασης. Όπως
βλέπουμε, το πλάτος γίνεται μέγιστο,
όταν η κυκλική συχνότητα ω γίνει
|
Σχήμα 5.6: Εξάρτηση του πλάτους Ι0 από την κυκλική
συχνότητα ω. |
![]() [5.23],
[5.23],
όταν δηλαδή η επαγωγική αντίσταση RL = ωL γίνει ίση με την
χωρητική RC = 1/ (ωC).
Τότε έχουμε το φαινόμενο του συντονισμού.
Η συχνότητα ![]() χαρακτηρίζεται
ως ιδιοσυχνότητα του κυκλώματος.
χαρακτηρίζεται
ως ιδιοσυχνότητα του κυκλώματος.
|
Σχήμα 5.7: Εξάρτηση της διαφοράς φάσεως φ από την
κυκλική συχνότητα. |
Όπως προκύπτει εξάλλου
από τις παραπάνω σχέσεις, η διαφορά φάσεως μεταξύ ρεύματος και τάσεως σε κατάσταση
συντονισμού μηδενίζεται.
Η συμπεριφορά
της διαφοράς φάσεως φ συναρτήσει της κυκλικής συχνότητας ω αποδίδεται ποιοτικά
στο σχήμα 5.7. Όπως βλέπουμε, για μικρές συχνότητες υπερισχύει η χωρητική αντίσταση και το κύκλωμα εμφανίζει χωρητική
συμπεριφορά: το ρεύμα προηγείται της τάσεως.
Για μεγάλες
συχνότητες υπερισχύει η επαγωγική
αντίσταση και το κύκλωμα εμφανίζει επαγωγική συμπεριφορά: το ρεύμα καθυστερεί.
Σε συντονισμό το
κύκλωμα εμφανίζει καθαρά ωμική συμπεριφορά: το ρεύμα είναι συμφασικό προς την
τάση.
5.5 Ισχύς και ενεργές τιμές εναλλασσομένων ρευμάτων
Η στιγμιαία
ισχύς P ενός εναλλασσομένου ρεύματος ![]() , το οποίο προκαλείται από την εναλλασσόμενη τάση
, το οποίο προκαλείται από την εναλλασσόμενη τάση ![]() , ισούται με το γινόμενο της (στιγμιαίας τιμής) της
τάσεως και της (στιγμιαία τιμή) εντάσεως:
, ισούται με το γινόμενο της (στιγμιαίας τιμής) της
τάσεως και της (στιγμιαία τιμή) εντάσεως:
στιγμιαία ισχύς: ![]() [ 5.24 ]
[ 5.24 ]
Λόγω της
διαρκούς μεταβολής της με τον χρόνο, η στιγμιαία ισχύς Ρ έχει ελάχιστη πρακτική
αξία. Αντιθέτως άμεσο πρακτικό ενδιαφέρον έχει η μέση ισχύς ![]() , η οποία υπολογίζεται ως εξής:
, η οποία υπολογίζεται ως εξής:
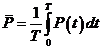 Þ
Þ ![]() : μέση ή ενεργός
ή πραγματική ισχύς [5.26]
: μέση ή ενεργός
ή πραγματική ισχύς [5.26]
όπου cosφ = συντελεστής
ισχύος: χαρακτηριστικό για το κύκλωμα μέγεθος.
Στην περίπτωση
που το εναλλασσόμενο ρεύμα διαρρέει μια ωμική αντίσταση R η μέση του ισχύς γίνεται: ![]() {1}
{1}
Αν η ίδια
αντίσταση διαρρέετο από συνεχές ρεύμα έντασης ![]() , τότε η αντίστοιχη ισχύς
, τότε η αντίστοιχη ισχύς ![]() θα ήταν ίση με την μέση ισχύ του εναλλασσομένου ρεύματος.
Η τιμή αυτή της έντασης χαρακτηρίζεται ως εκ τούτου ως ενεργός ένταση Ι
του εναλλασσομένου ρεύματος, η δε αυτήν προκαλούσα συνεχής τάση
θα ήταν ίση με την μέση ισχύ του εναλλασσομένου ρεύματος.
Η τιμή αυτή της έντασης χαρακτηρίζεται ως εκ τούτου ως ενεργός ένταση Ι
του εναλλασσομένου ρεύματος, η δε αυτήν προκαλούσα συνεχής τάση ![]() , ως ενεργός τάση αυτού:
, ως ενεργός τάση αυτού:
Ενεργός ένταση Ι εναλλασσομένου ρεύματος
καλείται η τιμή του συνεχούς εκείνου ρεύματος, το οποίο -όταν διαρρέει την
ίδια ωμική αντίσταση με το εναλλασσόμενο- αποδίδει ισχύ ίση με την μέση
ισχύ του εναλλασσομένου.
Ενεργά μεγέθη
εναλλασσομένου ρεύματος:![]() [5.27]
[5.27]
Με την βοήθεια
των ενεργών μεγεθών η σχέση [ 5.26 ] γράφεται:
![]() {2}
{2}
Από το νόμο του Ohm έχουμε εξάλλου: ![]() [5.28]
[5.28]
Συνοψίζοντας
λοιπόν τις παραπάνω σχέσεις έχουμε:
![]() [5.26α]
[5.26α]
μέση ή ενεργός ή
πραγματική ισχύς
6.1 Μαγνήτιση και μαγνητική διέγερση
Διαπερατότητα μ ενός υλικού
καλείται ο λόγος της μαγνητικής έντασης Β του μαγνητικού πεδίου (π.χ. ενός
σωληνοειδούς) παρουσία του υλικού (π.χ. με την μορφή πυρήνα στο εσωτερικό του
σωληνοειδούς) προς την ένταση Β0 του μαγνητικού πεδίου απουσία του
υλικού:
διαπερατότητα : ![]() [6.1]
[6.1]
Η διαπερατότητα μ είναι καθαρός αριθμός και η τιμή της εξαρτάται από την
φύση του υλικού και την θερμοκρασία του, χωρίς το τελευταίο να είναι απόλυτο.
Ανάλογα με την
τιμή της διαπερατότητας τους τα διάφορα υλικά κατατάσσονται στις ακόλουθες
τρεις κατηγορίες:
·
διαμαγνητικά: μ »< 1 ® εξασθενίζουν
ελαφρώς το πεδίο (π.χ. χαλκός, μόλυβδος, νερό)
·
παραμαγνητικά: μ »> 1 ® ενισχύουν
ελαφρώς το πεδίο (π.χ. πλατίνα, αλουμίνιο, μαγνήσιο)
·
σιδηρομαγνητικά: μ >> 1 ® ενισχύουν
αισθητά το πεδίο (σίδηρος, κοβάλτιο, νικέλιο)
(Σημειωτέον ότι
εκτός των τριών αυτών κατηγοριών, διακρίνουμε ακόμη τα λεγόμενα αντισιδηρομαγνητικά
και σιδηριμαγνητικά υλικά. Βλ. κεφ. 6.5)
Στον παρακάτω
Πίνακα περιέχονται οι τιμές της διαπερατότητας ορισμένων δια- και παραμαγνητικών
υλικών.
|
Πίνακας
6.1:
Διαπερατότητα ορισμένων υλικών |
|||
|
Διαμαγνητικά |
Παραμαγνητικά |
||
|
Βισμούθιο: |
0,999843 |
Πλατίνα: |
1,000256 |
|
Μόλυβδος: |
0,999984 |
Βολφράμιο: |
1,000068 |
|
Χαλκός: |
0,999990 |
Αλουμίνιο: |
1,000024 |
|
Νερό |
0,999991 |
Ταντάλιο: |
1,000018 |
Όταν λοιπόν στο εσωτερικό
ενός σωληνοειδούς εισαχθεί πυρήνας από κάποιο υλικό, η ένταση του μαγνητικού
πεδίου του σωληνοειδούς θα αυξηθεί ή θα μειωθεί ισόποσα προς την τιμή της
διαπερατότητας του συγκεκριμένου υλικού, χωρίς να μεταβληθεί η ένταση
του διαρρέοντος το σωληνοειδές ρεύμα. Το φαινόμενο αυτό σε συνδυασμό με το
γεγονός, ότι η εμφάνιση ενός μαγνητικού πεδίου προϋποθέτει την ύπαρξη ηλεκτρικών
ρευμάτων, μας οδηγεί στην λογική υπόθεση της εμφάνισης τέτοιων ρευμάτων στην
επιφάνεια του πυρήνα. Τα επιφανειακά αυτά ρεύματα δημιουργούν ένα επιπλέον
μαγνητικό πεδίο ![]() , το οποίο ανάλογα με τον προσανατολισμό του
ενισχύει ή εξασθενίζει το αρχικό πεδίο
, το οποίο ανάλογα με τον προσανατολισμό του
ενισχύει ή εξασθενίζει το αρχικό πεδίο ![]() του σωληνοειδούς:
του σωληνοειδούς:
![]() {1}
{1}
Τα εν λόγω
επιφανειακά ρεύματα είναι το μακροσκοπικό αποτέλεσμα του προσανατολισμού
στοιχειωδών κυκλικών ρευμάτων, τα οποία είναι άμεσα συνδεμένα με μικροσκοπική –
σε ατομική κλίμακα - δομή της
ύλης και καλούνται γι’ αυτό ατομικά κυκλικά ρεύματα. Πολλές φορές
χαρακτηρίζονται και σαν ρεύματα Ampere, από το όνομα του ερευνητή, ο οποίος τα
εισήγαγε πρώτος, προκειμένου να εξηγήσει τις μαγνητικές ιδιότητες της ύλης.
Τέτοια ατομικά
κυκλικά ρεύματα είναι για παράδειγμα οι τροχιές των ηλεκτρονίων γύρω από
τους πυρήνες των ατόμων.
Η μεταβολή ![]() της έντασης του
μαγνητικού πεδίου εξ αιτίας της παρουσίας του υλικού καλείται και μαγνητική
πόλωση
της έντασης του
μαγνητικού πεδίου εξ αιτίας της παρουσίας του υλικού καλείται και μαγνητική
πόλωση ![]() .
.
Η εξίσωση {1}
μπορεί να μετασχηματισθεί με την βοήθεια των παρακάτω διανυσματικών μεγεθών:
1.
μαγνητική διέγερση: 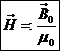 [6.2]
[6.2]
όπου ![]() : μαγνητική σταθερή πεδίου
: μαγνητική σταθερή πεδίου
2.
μαγνήτιση ενός υλικού: 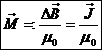 [6.3]
[6.3]
Με την βοήθεια
της μαγνητική διέγερσης και της μαγνήτισης η σχέση {1} γράφεται:
![]() [6.4]
[6.4]
Από τις παραπάνω
σχέσεις προκύπτει:
![]() [6.5]
[6.5]
![]() [6.6]
[6.6]
όπου χ = μ-1 : μαγνητική επιδεκτικότητα του
συγκεκριμένου υλικού:
διαμαγνητικά: χ »< Ο (![]() )
)
παραμαγνητικά: χ »> Ο (![]() )
)
σιδηρομαγνητικά: χ >>
0 (Εξαρτάται αποφασιστικά
από την προϊστορία του υλικού)
6.3 Διαμαγνητισμός και παραμαγνητισμός
Η ύπαρξη της
τροχιακής μαγνητικής ροπής των ηλεκτρονίων δεν συνεπάγεται κατ' ανάγκη και
την ύπαρξη μη μηδενικής μαγνητικής ροπής των αντιστοίχων ατόμων! Αυτό γίνεται
κατανοητό, αν σκεφθούμε, ότι σε περίπτωση απουσίας εξωτερικού μαγνητικού πεδίου
οι μαγνητικές ροπές των ηλεκτρονίων θα είναι προφανώς στατιστικά κατανεμημένες.
Όταν όμως το υλικό
βρεθεί μέσα σ’ ένα εξωτερικό μαγνητικό πεδίο, τότε επί των ατομικών μαγνητικών
δίπολων αναπτύσσεται μηχανική ροπή, η οποία τείνει να τα προσανατολίσει, προς
την κατεύθυνση του πεδίου. Η προκύπτουσα μαγνήτιση έχει την φορά του εξωτερικού
πεδίου, το οποίο και ενισχύει. Επομένως το υλικό συμπεριφέρεται ως παραμαγνητικό.
Αντιθέτως η
μαγνήτιση ![]() των διαμαγνητικών
υλικών είναι αντίθετη προς την μαγνητική διέγερση
των διαμαγνητικών
υλικών είναι αντίθετη προς την μαγνητική διέγερση ![]() και την
εξασθενίζει. Το γεγονός αυτό οφείλεται στο ότι η
μαγνήτιση των διαμαγνητικών υλικών δεν είναι προσανατολιζόμενη αλλά επαγόμενη.
Είναι δηλαδή αποτέλεσμα μικροσκοπικών επαγωγικών ρευμάτων, τα οποία επάγονται
στο εσωτερικό ενός υλικού, όταν αυτό βρεθεί κάτω από την επίδραση ενός εξωτερικού
μαγνητικού πεδίου. Ως επαγωγικά τα ρεύματα αυτά έχουν τέτοια φορά ώστε να στο
αίτιο που τα δημιούργησε και που είναι φυσικά το εξωτερικό μαγνητικό πεδίο.
Έτσι εξηγείται ποιοτικά και το γεγονός, ότι τα
διαμαγνητικά υλικά απωθούνται ελαφρώς από το (εξωτερικό) μαγνητικό πεδίο.
και την
εξασθενίζει. Το γεγονός αυτό οφείλεται στο ότι η
μαγνήτιση των διαμαγνητικών υλικών δεν είναι προσανατολιζόμενη αλλά επαγόμενη.
Είναι δηλαδή αποτέλεσμα μικροσκοπικών επαγωγικών ρευμάτων, τα οποία επάγονται
στο εσωτερικό ενός υλικού, όταν αυτό βρεθεί κάτω από την επίδραση ενός εξωτερικού
μαγνητικού πεδίου. Ως επαγωγικά τα ρεύματα αυτά έχουν τέτοια φορά ώστε να στο
αίτιο που τα δημιούργησε και που είναι φυσικά το εξωτερικό μαγνητικό πεδίο.
Έτσι εξηγείται ποιοτικά και το γεγονός, ότι τα
διαμαγνητικά υλικά απωθούνται ελαφρώς από το (εξωτερικό) μαγνητικό πεδίο.
Ενώ η θερμική
κίνηση αντιστέκεται στον προσανατολισμό των μονίμων («παραμαγνητικών») δίπολων,
αφήνει ανεπηρέαστη την επαγωγή («διαμαγνητικών») μαγνητικών δίπολων. Ως εκ τούτου
·
η μαγνητική επιδεκτικότητα των
διαμαγνητικών υλικών είναι ανεξάρτητη από την θερμοκρασία, ενώ
·
η μαγνητική επιδεκτικότητα των
παραμαγνητικών υλικών ελαττώνεται με αυξανόμενη θερμοκρασία.
Η εξάρτηση της
παραμαγνητικής επιδεκτικότητας από την θερμοκρασία δίδεται από τον
παρακάτω, εμπειρικό νόμο του Curie:
νόμος του Curie: ![]() [6.7]
[6.7]
όπου C : σταθερά του Curie
|
Σχήμα 6.2: Περιοχές Weiss. |
Ο σιδηρομαγνητισμός οφείλεται στην
ιδιοπεριστροφική κίνηση (spin) των ηλεκτρονίων και την αντίστοιχη μαγνητική διπολική
ροπή. Συγκεκριμένα - και όπως αποδεικνύεται στα πλαίσια της Κβαντομηχανικής και
μόνο - η ηλεκτροστατική ενέργεια των ηλεκτρονίων ορισμένων υλικών γίνεται
ελάχιστη, όταν τα spin τους είναι παράλληλα και ομόρροπα. Στις περιπτώσεις αυτές τα ηλεκτρονικά spin και οι αντίστοιχες
ιδιοπεριστροφικές μαγνητικές διπολικές ροπές προσανατολίζονται φυσικά ομαδικά
προκειμένου να μειωθεί η ενέργεια του συστήματος. Χωρίς εξωτερικό μαγνητικό
πεδίο τα ηλεκτρονικά spin δεν προσανατολίζονται ομοιόμορφα σε όλη
την μάζα του συγκεκριμένου υλικού, αλλά μόνο σε πολύ μικρότερες (πάντως
μακροσκοπικές) περιοχές, τις ονομαζόμενες περιοχές Weiss.
|
Σχήμα 6.3: Τεχνικό διάγραμμα μαγνητίσεως. |
Το διπλανό διάγραμμα, στο οποίο παριστάνεται
γραφικά η μαγνήτιση Μ, την οποία αποκτά ένα σιδηρομαγνητικό υλικό κάτω από την
επίδραση εξωτερικού μαγνητικού πεδίου, συναρτήσει της μαγνητικής διέγερσης Η
του πεδίου καλείται τεχνικό διάγραμμα μαγνητίσεως.
Η καμπύλη 0 ® 1 καλείται παρθενική καμπύλη,
παρατηρείται μόνο την πρώτη φορά, κατά την οποία το υλικό δέχεται την επίδραση
εξωτερικού μαγνητικού πεδίου. Η αύξηση της μαγνήτισης με αυξανόμενη μαγνητική
διέγερση οφείλεται αρχικά στην αύξηση του όγκου εκείνων των περιοχών Weiss, των οποίων ο
προσανατολισμός είναι ο πλησιέστερος προς την διεύθυνση και φορά της μαγνητικής
διέγερσης, σε βάρος των υπολοίπων. Όταν ολοκληρωθεί το φαινόμενο αυτό, οπότε η
διεύθυνση και φορά της μαγνήτισης είναι η ίδια για όλο τον όγκο του υλικού,
παραπέρα αύξηση του εξωτερικού πεδίου προκαλεί βαθμιαίο προσανατολισμό όλων
των στοιχειωδών μαγνητικών δίπολων, έως ότου επέλθει (σημείο 1 του διαγράμματος
6.3) κορεσμός. Στην κατάσταση αυτή ομιλούμε για μαγνήτιση κορεσμού
και ένταση κορεσμού.
Αν αρχίσουμε,
ξεκινώντας από την κατάσταση κορεσμού 1, να ελαττώνουμε την μαγνητική διέγερση,
παρατηρούμε ότι η μαγνήτιση δεν
επανέρχεται μέσω της παρθενικής καμπύλης 1 ® 0, αλλά παραμένει μεγαλύτερη από τις τιμές της καμπύλης
αυτής. Το φαινόμενο αυτό καλείται μαγνητική υστέρηση. Έτσι και
όταν ακόμη μηδενισθεί το εξωτερικό μαγνητικό πεδίο Β0, το υλικό
παραμένει μαγνητισμένο, αποτελώντας έναν μόνιμο μαγνήτη, ο οποίος
δημιουργεί μαγνητικό πεδίο εντάσεως ![]() .
.
Αν
αντιστρέψουμε την φορά της μαγνητικής διέγερσης ![]() , και μεταβάλουμε την τιμή όπως και πριν, θα διαγράψουμε
τελικά έναν κλειστό βρόγχο, 1 ® 2 ® 3 ® 4 ® 5 ® 6 ® 1, τον λεγόμενο βρόγχο μαγνητικής υστέρησης. Ανάλογα
με το πλάτος του βρόγχου υστερήσεως τα σιδηρομαγνητικά υλικά κατατάσσονται σε
μαγνητικά μαλακά (στενός βρόγχος) και μαγνητικά σκληρά
(πλατύς βρόγχος).
, και μεταβάλουμε την τιμή όπως και πριν, θα διαγράψουμε
τελικά έναν κλειστό βρόγχο, 1 ® 2 ® 3 ® 4 ® 5 ® 6 ® 1, τον λεγόμενο βρόγχο μαγνητικής υστέρησης. Ανάλογα
με το πλάτος του βρόγχου υστερήσεως τα σιδηρομαγνητικά υλικά κατατάσσονται σε
μαγνητικά μαλακά (στενός βρόγχος) και μαγνητικά σκληρά
(πλατύς βρόγχος).
Ο αυθόρμητος
προσανατολισμός των spins στις περιοχές Weiss καταστρέφεται, όταν η θερμική κίνηση ξεπεράσει ένα χαρακτηριστικό για το
υλικό όριο, το οποίο αντιστοιχεί στην λεγομένη θερμοκρασία Curie ΤC. . Για
θερμοκρασίες μεγαλύτερες αυτής της κρίσιμης θερμοκρασίας το σιδηρομαγνητικό
υλικό συμπεριφέρεται ως παραμαγνητικό με επιδεκτικότητα:
![]() : Νόμος των Curie – Weiss [6.8]
: Νόμος των Curie – Weiss [6.8]
6.5 Αντισιδηρομαγνητισμός και σιδηριμαγνητισμός
Ενώ ο
σιδηρομαγνητισμός οφείλεται στην παράλληλη διάταξη των ηλεκτρονικών spins, υπάρχουν
υλικά, στα οποία (και πάλι για καθαρά ενεργειακούς λόγους) έχουμε αντιπαράλληλη
διάταξη των ηλεκτρονικών spins γειτονικών ατόμων. Αυτό έχει ως αποτέλεσμα την
αλληλοεξουδετέρωοη των αντιστοίχων μαγνητικών ροπών, οπότε το αντισιδηρομαγνητικό, όπως
χαρακτηρίζεται, υλικό παρουσιάζει διαμαγνητική συμπεριφορά, παρά το γεγονός ότι
αποτελείται από «παραμαγνητικά» άτομα. Η αντιπαράλληλη διάταξη των spins καταρρέει όμως
σε μια χαρακτηριστική για το υλικό θερμοκρασία Neel, υπεράνω της
οποίας το υλικό εμφανίζει παραμαγνητική συμπεριφορά.
Στην περίπτωση
που ένας κρύσταλλος αποτελείται από διαφορετικά ιόντα η αντιπαράλληλη διάταξη
δεν εξουδετερώνει πλήρως τις μαγνητικές ροπές. Έτσι τα συγκεκριμένα υλικά
συμπεριφέρονται παρόμοια με τα σιδηρομαγνητικά, έχουν όμως πολύ μικρότερη μαγνήτιση
κορεσμού. Τέτοια
υλικά καλούνται σιδηριμαγνητικά υλικά.
6.6 Εφαρμογές
Η μαγνήτιση ενός
υλικού συνεπάγεται μια μικρή μεταβολή των ατομικών αποστάσεων με αποτέλεσμα
την μεταβολή του όγκου του μαγνητισθέντος υλικού. Το φαινόμενο αυτό καλείται
μαγνητοσυστολή και αξιοποιείται για την δημιουργία υπερήχων.
2. Ψύξη μέσω αδιαβατικής
απομαγνήτισης
Η μέθοδος αυτή
στηρίζεται στο γεγονός, ότι τα στοιχειώδη μαγνητικά δίπολα ενός παραμαγνητικού
υλικού προσανατολίζονται μερικώς, όταν δεχτούν την επίδραση ενός εξωτερικού
μαγνητικού πεδίου. Ο προσανατολισμός αυτός έχει ως αποτέλεσμα την ελάττωση της εντροπίας
του συστήματος. Χωρίς την επίδραση του εξωτερικού μαγνητικού πεδίου, η παραπάνω
ελάττωση της εντροπίας θα μπορούσε να επιτευχθεί μόνο μέσω ελάττωσης της
θερμοκρασίας του συστήματος. Κάτω λοιπόν από την επίδραση του εξωτερικού
μαγνητικού πεδίου η εντροπία του συστήματος παίρνει μία τιμή, η οποία
αντιστοιχεί στην τάξη, η οποία επικρατεί σε χαμηλότερη θερμοκρασία, όταν επί
του συστήματος δεν επιδρά εξωτερικό μαγνητικό πεδίο.
Αν μηδενίσουμε το
πεδίο, η επιτευχθείσα τάξη θα καταστραφεί λόγω της ροής θερμικής ενέργειας από
το περιβάλλον, εκτός και αν φροντίσουμε για επαρκή θερμομόνωση του συστήματος
και το απομαγνητίσουμε αδιαβατικά: τότε δεν είναι δυνατή η ροή θερμικής ενέργειας
από το περιβάλλον, οπότε η επιτευχθείσα τάξη διατηρείται με αποτέλεσμα την
ελάττωση της θερμοκρασίας του συστήματος.
ΣΩΜΑΤΙΔΙΑ - ΑΚΤΙΝΟΒΟΛΙΕΣ
Όλα τα μέχρι
σήμερα γνωστά υλικά αποτελούνται από μικροσκοπικές μονάδες, τα άτομα,
ή συγκροτήματα ατόμων, τα μόρια. Οι μικροσκοπικές αυτές
μονάδες αποτελούν την ελάχιστη δυνατή ποσότητα ύλης, η οποία εξακολουθεί να
έχει τις ίδιες χημικές ιδιότητες με το υπό εξέταση υλικό. Αν δηλαδή τις
διασπάσουμε (π.χ. μέσω βομβαρδισμού με άλλα σωματίδια), θα διαπιστώσουμε, ότι
τα θραύσματα έχουν εντελώς διαφορετικές ιδιότητες από τα συγκεκριμένα
άτομα (ή μόρια). Εξάλλου αξιοσημείωτο είναι το γεγονός, ότι όλα τα άτομα ενός
συγκεκριμένου στοιχείου είναι πανομοιότυπα μεταξύ τους.
6.8 Δομή και χαρακτηρισμός των ατόμων
Όπως διαπιστώθηκε
με την βοήθεια πειραμάτων σκέδασης, κατά τα οποία βομβαρδίζουμε ένα υλικό με
διάφορα ηλεκτρικώς φορτισμένα ή μη σωματίδια και παρατηρούμε την σκέδαση τους,
τα άτομα αποτελούνται από έναν κεντρικό πυρήνα και από έναν
αριθμό περί τον πυρήνα περιφερόμενων ηλεκτρονίων, τα οποία συνθέτουν το ατομικό
περίβλημα. Τα κύρια χαρακτηριστικά της σήμερα παραδεκτής δομής του
ατόμου αποδίδονται σχηματικά στο παρακάτω διάγραμμα.
ΔΟΜΗ ΤΟΥ ΑΤΟΜΟΥ
σχηματικά
άτομο


![]()
![]() πυρήνας ατομικό περίβλημα
πυρήνας ατομικό περίβλημα
νουκλεόνια
![]()
πρωτόνια ουδετερόνια ηλεκτρόνια
(ή νετρόνια)
|
φορτίο: |
|
0 |
-e |
|
μάζα: |
1836me |
1839 me |
|
|
σύμβολο: |
|
|
e- |
Όπως φαίνεται
από το παραπάνω διάγραμμα, ο πυρήνας αποτελείται από πρωτόνια (θετικώς
με ένα στοιχειώδες ηλεκτρικό φορτίο φορτισμένα σωματίδια, σύμβολο ![]() ) και ουδετερόνια (ηλεκτρικώς ουδέτερα -
όπως φανερώνει και το όνομα τους - σωματίδια, σύμβολο
) και ουδετερόνια (ηλεκτρικώς ουδέτερα -
όπως φανερώνει και το όνομα τους - σωματίδια, σύμβολο ![]() ). Γύρω από τον πυρήνα περιφέρονται τόσα ηλεκτρόνια
(φορτίο ίσο και αντίθετο με εκείνο του πρωτονίου, αμελητέα μάζα, σύμβολο e-), όσα και τα
εντός του πυρήνος πρωτόνια. Έτσι τα άτομα είναι υπό κανονικές συνθήκες
ηλεκτρικώς ουδέτερα.
). Γύρω από τον πυρήνα περιφέρονται τόσα ηλεκτρόνια
(φορτίο ίσο και αντίθετο με εκείνο του πρωτονίου, αμελητέα μάζα, σύμβολο e-), όσα και τα
εντός του πυρήνος πρωτόνια. Έτσι τα άτομα είναι υπό κανονικές συνθήκες
ηλεκτρικώς ουδέτερα.
Ο πυρήνας
συγκεντρώνει το σύνολο σχεδόν της μάζας του ατόμου παρά το γεγονός, ότι η
διάμετρός του (~ 10-![]() , δηλαδή σε εκατό εκατομμύρια τόνους ανά κυβικό εκατοστόμετρο!
, δηλαδή σε εκατό εκατομμύρια τόνους ανά κυβικό εκατοστόμετρο!
Για τον
χαρακτηρισμό των ατόμων χρησιμοποιείται ο ακόλουθος, συμβολικός τρόπος γραφής:
όπου Ζ = ατομικός αριθμός =
αριθμός πρωτονίων του πυρήνος = αριθμός ηλεκτρονίων του ατομικού περιβλήματος,
όταν το άτομο είναι ουδέτερο.
Α = μαζικός αριθμός = αριθμός νουκλεονίων του πυρήνος
Π.χ. ![]()
Όταν
αναφερόμαστε σε έναν συγκεκριμένο πυρήνα χωρίς να μας ενδιαφέρει το ατομικό
περίβλημα, χρησιμοποιούμε συχνά τον όρο «νουκλίδιο»
6.9 Ισότοπα
Οι χημικές ιδιότητες
ενός στοιχείου καθορίζονται από τον αριθμό των ηλεκτρονίων του, ο οποίος -όπως
προαναφέραμε- πάντα για ουδέτερα εννοείται άτομα είναι ίσος με εκείνον των
πρωτονίων του πυρήνα. Επομένως στοιχεία με τον ίδιο αριθμό πρωτονίων έχουν τις
ίδιες χημικές ιδιότητες, ακόμη και αν έχουν διαφορετικό αριθμό ουδετερονίων.
Επειδή λοιπόν τα στοιχεία αυτά βρίσκονται στην ίδια θέση του Περιοδικού Πίνακα
(στον οποίο ως γνωστόν κατατάσσουμε τα διάφορα χημικά στοιχεία σύμφωνα με τον
ατομικό τους αριθμό και άρα σύμφωνα με τις χημικές τους ιδιότητες), καλούνται
ισότοπα : Τα ισότοπα ενός
στοιχείου διαφέρουν ως προς τον αριθμό των πρωτονίων.
Π.χ.
Μερικά από τα ισότοπα του Ουρανίου:
|
άτομο |
πρωτόνια |
ουδετερόνια |
συχνότητα
εμφάνισης στη φύση |
|
|
92 |
142 |
0,0057% |
|
|
92 |
143 |
0,72% |
|
|
92 |
146 |
99,27% |
6.10 Μάζα και διαστάσεις των ατόμων
Όταν μιλάμε για
την μάζα ενός ατόμου, αναφερόμαστε συνήθως στην σχετική μάζα Μ, η
οποία μας δείχνει πόσο μεγαλύτερη είναι η (απόλυτη) μάζα του συγκεκριμένου
ατόμου, από το 1/12 της (απόλυτης) μάζας του ατόμου του άνθρακα ![]() .
.
Η παραπάνω
(σχετική) μάζα αναφέρεται δε συνήθως λανθασμένα ως «ατομικό βάρος», εξ
αιτίας της σύγχυσης η οποία επικρατεί, όσον αφορά την σημασία των όρων «μάζα»
και «βάρος».
Η σχετική μάζα
του ελαφρύτερου στοιχείου, του Υδρογόνου, είναι 1,008, ενώ του βαρύτερου, του Ουρανίου, 238,03.[2]
Η απόλυτη μάζα μετράται σε kg. Για λόγους δε
σκοπιμότητας (βλ. παραπάνω) έχει εισαχθεί η ατομική μονάδα μάζας u, η οποία ισούται
με το 1/12 της απόλυτης μάζας του ισοτόπου ![]() :
:
ατομική μονάδα μάζας: ![]() (ή
(ή ![]() )
)
Η απόλυτη μάζα m ενός ατόμου υπολογίζεται πολλαπλασιάζοντας την σχετική του μάζα Μ με την
ατομική μονάδα μάζας:
![]() [7.1]
[7.1]
Η διάμετρος τώρα
του ατόμου αναφέρουμε απλώς, ότι -όπως προκύπτει από έγκυρες πειραματικές
μετρήσεις– είναι της τάξεως των 10-10 m, ενώ η διάμετρος του πυρήνα της τάξεως
των 10-14 m.
Επειδή τα άτομα
διαφεύγουν -λόγω του μικροσκοπικού τους μεγέθους- της άμεσης παρατήρησης, η
μόνη δυνατότητα περιγραφής της δομής τους είναι η χρήση «ατομικών μοντέλων».
Τα μοντέλα αυτά «ζουν και πεθαίνουν» ανάλογα με την ικανότητα τους να εξηγούν
την μακροσκοπική, παρατηρήσιμη συμπεριφορά των ατόμων. Έτσι βρίσκονται σε
διαρκή εξέλιξη και βελτίωση. Ας δούμε λοιπόν τα κυριότερα εξ αυτών:
Μοντέλο του Rutherford: Τα ηλεκτρόνια περιστρέφονται γύρω από
τον πυρήνα, όπως οι πλανήτες γύρω από τον ήλιο. Με άλλα λόγια, το άτομο
αποτελεί ένα είδος μικροσκοπικού πλανητικού συστήματος, στο οποίο όμως τον
ρόλο της κεντρομόλου δυνάμεως παίζει η ελκτική δύναμη Coulomb μεταξύ του θετικού πυρήνα και
των αρνητικών ηλεκτρονίων, και όχι η συντριπτικά ασθενέστερη βαρυτική έλξη.
Σύμφωνα τώρα με
τους νόμους της Ηλεκτροδυναμικής το κεντρομόλως επιταχυνόμενο, όπως και κάθε
επιταχυνόμενο ηλεκτρικό φορτίο, θα έπρεπε να ακτινοβολεί διαρκώς ενέργεια. Το
γεγονός αυτό θα είχε ως αποτέλεσμα την διαρκή ελάττωση της δυναμικής και
κινητικής ενέργειας του ηλεκτρονίου. Έτσι το ηλεκτρόνιο θα έπεφτε μέσα σε
ελάχιστο χρόνο επί του πυρήνα διαγράφοντας μια σπειροειδή τροχιά. Το άτομο του Rutherford είναι επομένως ασταθές.
Μοντέλο του Bohr: Ο Bohr επέκτεινε το
μοντέλο του Rutherford προκειμένου να
εξηγήσει την ευστάθεια του ατόμου και την εκπομπή ακτινοβολίας
συγκεκριμένων διακριτών συχνοτήτων. Προς τον σκοπό αυτό εισήγαγε δύο συνθήκες, οι
οποίες κινούνταν έξω από τα πλαίσια της κλασικής Φυσικής και βρήκαν την εξήγηση
τους αργότερα μέσω της Κβαντομηχανικής.
1η
Συνθήκη του Bohr: Τα ηλεκτρόνια ενός ατόμου κινούνται
χωρίς να ακτινοβολούν επί συγκεκριμένων (κυκλικών) τροχιών, οι οποίες καλούνται
σταθερές ή επιτρεπόμενες και καθορίζονται από την επόμενη κβαντική
συνθήκη:
Η
στροφορμή ενός γύρω από τον πυρήνα περιστρεφόμενου ηλεκτρονίου είναι ακέραιο
πολλαπλάσιο της ποσότητας ![]() :
: ![]() [
7.2 ]
[
7.2 ]
όπου L = τροχιακή στροφορμή ηλεκτρονίου
m = μάζα
ηλεκτρονίου
r = ακτίνα διαγραφομένης τροχιάς
v = ταχύτητα
ηλεκτρονίου
n = 1,2,3... =
κύριος κβαντικός αριθμός
![]() , h = 6,626 · 10-34 Js : σταθερή
του Plank.
, h = 6,626 · 10-34 Js : σταθερή
του Plank.
2η Συνθήκη
του Bohr: Ένα άτομο εκπέμπει ένα φωτόνιο
ηλεκτρομαγνητικής ακτινοβολίας, όταν ένα ηλεκτρόνιο μεταπηδά από μια τροχιά
μεγαλύτερου κύριου κβαντικού αριθμού σε μια τροχιά μικρότερου κύριου κβαντικού
αριθμού. Η ενέργεια δε του εκπεμπόμενου φωτονίου ισούται με την διαφορά της
τελικής από την αρχική ενέργεια του ηλεκτρονίου:
![]() [7.3]
[7.3]
όπου Ε = ενέργεια εκπεμπόμενου φωτονίου
ν = εκπεμπόμενης ακτινοβολίας
Εαρχ = ολική αρχική ενέργεια ηλεκτρονίου
Ετελ = ολική τελική ενέργεια ηλεκτρονίου
Το μοντέλο του Bohr παρά το
γεγονός, ότι μας επιτρέπει να υπολογίσουμε εύκολα και με ακρίβεια το φάσμα του
απλούστερου όλων των ατόμων, του Υδρογόνου, αδυνατεί να εξηγήσει π.χ.
την λεπτή υφή του φάσματος του Υδρογόνου: Αν εξετάσουμε το φάσμα
του Υδρογόνου με μεγαλύτερη ανάλυση, θα παρατηρήσουμε, ότι πολλές από τις
«γραμμές» του αποτελούνται από δύο ξεχωριστές γραμμές, ευρισκόμενες η μία κοντά
στην άλλη.
Προκειμένου να
αντιμετωπιστούν οι αδυναμίες αυτές ο Sommerfeld διεύρυνε το ατομικό
μοντέλο του Bohr εισάγοντας
εκτός της κυκλικής και ελλειπτικές τροχιές. Πιο συγκεκριμένα, σύμφωνα με τον Sommerfeld σε κάθε τιμή
του κύριου κβαντικού αριθμού αντιστοιχούν n τροχιές οι οποίες αριθμούνται μέσω του δευτερεύοντος
κβαντικού αριθμού l = 0,1,2…(n -1). Στην μέγιστη
τιμή του l (για δεδομένο n) αντιστοιχεί
πάντα μια κυκλική τροχιά, ενώ στις υπόλοιπες αντιστοιχούν ελλειπτικές τροχιές,
η εκκεντρότητα των οποίων αυξάνεται με ελαττούμενη τιμή του l.
Ένα ηλεκτρόνιο
κινούμενο επί μιας ελλειπτικής τροχιάς έχει μεγαλύτερη ταχύτητα στο πλησίον
του πυρήνα ευρισκόμενο τμήμα απ' ότι στο πιο απομακρυσμένο. Το γεγονός αυτό
συνεπάγεται - σύμφωνα με την θεωρία της Σχετικότητας - μια αντίστοιχη
αυξομείωση της μάζας του ηλεκτρονίου. Έτσι οι τροχιές του ηλεκτρονίου, οι
οποίες ανήκουν στον ίδιο κύριο κβαντικό αριθμό έχουν διαφορετικές ενέργειες.
Εκτός του κύριου
(n) και
δευτερεύοντος (l) κβαντικού αριθμού και προκειμένου να εξηγηθούν τα χαρακτηριστικά
πολυπλοκότερων φασμάτων εισήχθησαν άλλοι δύο κβαντικοί αριθμοί:
Ο μαγνητικός κβαντικός αριθμός m, ο οποίος
παίρνει τις (2l + 1) τιμές: -l, -l+1, ... 0 ...1,
....l, και περιγράφει
τον προσανατολισμό των τροχιών στον χώρο.
Ο κβαντικός αριθμός του spin s, ο οποίος
περιγράφει τον προσανατολισμό της ιδιοπεριστροφικής ορμής του ηλεκτρονίου σε σχέση
με την φορά της τροχιακής του ορμής.
Στα πλαίσια του
διευρυμένου (μέσω της εισαγωγής του μαγνητικού κβαντικού αριθμού και του
κβαντικού αριθμού του spin) μοντέλου των Bohr - Sommerfeld συνηθίζεται να θεωρούμε, ότι όλες οι τροχιές, οι
οποίες ανήκουν στον ίδιο κύριο κβαντικό αριθμό n (και οι οποίες έχουν χονδρικώς σχεδόν
την ίδια ενέργεια), αποτελούν έναν φλοιό. Για λόγους δε
ιστορικούς, ο εσωτερικός φλοιός (n=1) συμβολίζεται με το γράμμα K, ο αμέσως εξωτερικότερος (n=2) με το γράμμα
L, κ.ο.κ. Ο
αριθμός των τροχιών, οι οποίες περιέχονται σε κάθε φλοιό, προκύπτει από τις τιμές
των τεσσάρων κβαντικών αριθμών. Όπως δε φαίνεται και από τον Πίνακα 7.4.2
Ο φλοιός με τον κύριο κβαντικό αριθμό n περιέχει n2 τροχιές.
Η ταξινόμηση των
χημικών στοιχείων κατά αύξουσα ατομική μάζα καταδεικνύει μια περιοδικότητα των
χημικών ιδιοτήτων και οδήγησε ως γνωστόν στην δημιουργία του Περιοδικού Πίνακα
από τον Mendelejeff. Ο εν λόγω
πίνακας εξηγείται επακριβώς, αν δεχθούμε, ότι η δομή του ατομικού περιβλήματος
ακολουθεί τους παρακάτω δύο κανόνες:
α) Όλα τα
ηλεκτρόνια ενός ατόμου κινούνται επί εκείνων των επιτρεπομένων - σύμφωνα με το
διευρυμένο μοντέλο των Bohr -Sommerfeld («μοντέλο
των φλοιών»)- τροχιών, επί των οποίων έχουν την ελάχιστη δυνατή
ενέργεια.
|
Πίνακας 7.4.2: «Φλοιοί – τροχιές – ηλεκτρόνια» και κβαντικοί αριθμοί |
||
|
K n=1 l=0 m=0 |
μια κυκλική
τροχιά |
σε
κάθε τροχιά έχουμε δύο δυνατότητες προσανατολισμού του spin: παράλληλα
και αντιπαράλληλα προς την τροχιακή ορμή (δηλαδή |
|
L |
μια ελλειπτική και
τρεις κυκλικές τροχιές |
|
|
Μ |
μια πολύ έκκεντρη ελλειπτική τροχιά τρεις
ελλειπτικές τροχιές με μικρότερη εκκεντρότητα και πέντε κυκλικές
τροχιές |
|
β) Απαγορευτική
αρχή του Pauli: Δύο ηλεκτρόνια ενός ατόμου
πρέπει να διαφέρουν σε έναν τουλάχιστον κβαντικό αριθμό.
Σύμφωνα με την
απαγορευτική αρχή του Pauli σε κάθε τροχιά μπορούν να κινούνται δύο το πολύ
ηλεκτρόνια, των οποίων τα spin θα είναι αντιπαράλληλα. Αυτό σημαίνει, ότι οι n2 τροχιές του
φλοιού n μπορούν να
δεχτούν 2(n2) ηλεκτρόνια.
Το μοντέλο των
ατομικών φλοιών παραμένει ακόμη και σήμερα δημοφιλές κυρίως λόγω της
παραστατικότητάς του, αν και έχει αρκετές αδυναμίες. Π.χ. δεν εξηγεί την απαγορευτική
αρχή του Pauli, απλώς την
δέχεται αξιωματικά. Δεν εξηγεί τα κριτήρια μετάβασης από μια τροχιά σε άλλη,
δεν εξηγεί τις δύο τιμές του κβαντικού αριθμού του spin, δεν μπορεί καν να εξηγήσει το
φάσμα του Ηλίου, κ.λ.π. Όλες αυτές οι αδυναμίες ξεπερνιούνται μόνο στα πλαίσια
του κυματικού μοντέλου του ατόμου,
το οποίο είναι γέννημα θρέμμα της Κβαντομηχανικής.
Στα πλαίσια του
κυματομηχανικού μοντέλου του ατόμου οι τροχιές του Bohr αντικαθίστανται μέσω
τρισδιάστατων στάσιμων κυμάτων, έκαστο των οποίων έχει συγκεκριμένη ενέργεια
και συχνότητα και παριστάνει μια «κατάσταση» ενός ηλεκτρονίου. Έτσι στην θέση
της μεταπήδησης από μια τροχιά σε μια άλλη έρχεται η μετάβαση από μια κατάσταση
(» τρισδιάστατο στάσιμο κύμα) σε
μια άλλη. Η ένταση των παραπάνω κυμάτων
σε ένα σημείο του χώρου αποτελεί το μέτρο της πιθανότητας να βρίσκεται το
ηλεκτρόνιο στην συγκεκριμένη θέση.
6.12 Ο πυρήνας
Η μάζα ενός
πυρήνα μπορεί να προσδιοριστεί με πάρα πολύ μεγάλη ακρίβεια με την βοήθεια των φασματογράφων
μάζας. Από τέτοιου είδους ακριβείς μετρήσεις προκύπτει, ότι η μάζα ενός
ατομικού πυρήνα είναι πάντα μικρότερη από το άθροισμα των μαζών των νουκλεονίων,
εκ των οποίων αποτελείται:
Η διαφορά μάζας
Δm μεταξύ της μάζας ενός πυρήνα και του αθροίσματος των
μαζών των νουκλεονίων, εκ των οποίων αποτελείται ο συγκεκριμένος πυρήνας,
καλείται έλλειμμα μάζας.
Με άλλα λόγια,
όταν μεμονωμένα νουκλεόνια συνδέονται για την δημιουργία ενός πυρήνα, χάνουν
ένα μέρος της μάζας τους. Η μάζα αυτή δεν εξαφανίζεται, αλλά μετατρέπεται
-σύμφωνα με την αρχή ισοδυναμίας μεταξύ μάζας και ενέργειας- σε
ενέργεια. Η ενέργεια αυτή καλείται ενέργεια συνδέσεως W και
ελευθερώνεται κατά την συνένωση των νουκλεονίων σε έναν πυρήνα:
Ενέργεια
συνδέσεως W καλείται η ενέργεια, η οποία ελευθερούται κατά την
δημιουργία ενός πυρήνα από μεμονωμένα νουκλεόνια.
Αν αντιθέτως
θέλουμε να διασπάσουμε έναν πυρήνα σε μεμονωμένα νουκλεόνια, θα πρέπει να του
προσφέρουμε ενέργεια ίση προς την ενέργεια συνδέσεως.
Σύμφωνα με την
αρχή ισοδυναμίας μεταξύ μάζας και ενέργειας του Einstein, μεταξύ του
ελλείμματος μάζας και της ενέργειας συνδέσεως ισχύει η σχέση:
![]() [7.4
]
[7.4
]
όπου W = ενέργεια συνδέσεως
Δm = έλλειμμα
μάζας
c = 3 · 108
m/s = ταχύτητα του
φωτός στο κενό.
|
Σχήμα 7.1: Μέση ενέργεια συνδέσεως ανά νουκλεόνιο
συναρτήσει του μαζικού αριθμού Α. |
Σημειώνουμε ότι η ενέργεια συνδέσεως των διαφόρων πυρήνων είναι κατά
106 περίπου φορές μεγαλύτερη από την ενέργεια αναδιάταξης των
ηλεκτρονίων. Η ίδια αναλογία ισχύει επομένως και για την ενέργεια, η
οποία συνοδεύει τις πυρηνικές (διάσπαση του πυρήνα) και χημικές (π.χ. καύση
χημικών καυσίμων) αντιδράσεις αντίστοιχα.
Η ενέργεια
συνδέσεως διαφέρει από πυρήνα σε πυρήνα και αποτελεί ένα χαρακτηριστικό
μέγεθος για τον συγκεκριμένο πυρήνα. Ιδιαίτερο όμως πρακτικό ενδιαφέρον έχει η μέση
ενέργεια συνδέσεως ανά νουκλεόνιο: αν κατορθώσουμε να αυξήσουμε την
μέση ενέργεια συνδέσεως ανά νουκλεόνιο, κερδίζουμε την αύξηση ως εκλυόμενη
ενέργεια. Όπως τώρα φαίνεται στο σχήμα 7.1, την μεγαλύτερη (μέση) ενέργεια
συνδέσεως ανά νουκλεόνιο έχουν πυρήνες, των οποίων ο μαζικός αριθμός Μ είναι
γύρω στο 50. Επομένως:
Πυρηνική ενέργεια ελευθερούται κατά την συνένωση ελαφριών πυρήνων («πυρηνική
σύντηξη») ή κατά την διάσπαση βαρέων πυρήνων («πυρηνική διάσπαση»),
λόγω της αύξησης της μέσης ενέργειας συνδέσεως ανά νουκλεόνιο.
Μεταξύ των
νουκλεονίων (πρωτονίων και ουδετερονίων) του πυρήνα αναπτύσσονται δύο είδη
δυνάμεων: απωστικές δυνάμεις Coulomb μεταξύ των ομωνύμων πρωτονίων και ελκτικές δυνάμεις
μεταξύ όλων των νουκλεονίων, οι οποίες καλούνται ισχυρές πυρηνικές δυνάμεις
και είναι καθαρά κβαντομηχανικής φύσεως. Οι ελκτικές ισχυρές πυρηνικές δυνάμεις
είναι, όπως προδίδει και το όνομα τους, πολύ ισχυρότερες από τις απωστικές
δυνάμεις Coulomb, έχουν όμως
πολύ μικρή εμβέλεια (< 10-15
cm). Αντιθέτως οι δυνάμεις Coulomb έχουν άπειρη εμβέλεια. Αποτέλεσμα τούτου είναι η
αστάθεια των βαρύτερων και κατά συνέπεια ογκωδέστερων πυρήνων. Πιο συγκεκριμένα
πρόκειται για τους πυρήνες με ατομικό αριθμό μεγαλύτερο του 84. Οι πυρήνες
αυτοί διασπόνται λοιπόν αυθόρμητα εκπέμποντας την λεγόμενη ραδιενεργό
ακτινοβολία, φαινόμενο το οποίο χαρακτηρίζεται ως φυσική
ραδιενέργεια.
Η ραδιενεργός
ακτινοβολία αποτελείται από:
α) Σωματίδια
α = πυρήνες Ηλίου, αποτελούμενοι από δύο πρωτόνια και δύο ουδετερόνια.
β) Σωματίδια
β = ταχέως κινούμενα ηλεκτρόνια, η ταχύτητα τους μπορεί να
φτάσει μέχρι και το 99,9% της ταχύτητας του φωτός.
γ) Σωματίδια
γ = κβάντα ηλεκτρομαγνητικής
ακτινοβολίας πολύ μεγάλης (~ 1020
Hz) συχνότητας, άρα
και ενέργειας.
Πειραματικές
μετρήσεις έδειξαν, ότι ο αριθμός dΝ των πυρήνων, οι οποίοι διασπώνται μέσα σε χρόνο dt, είναι ανάλογος
του αριθμού N των κατά την
δεδομένη χρονική στιγμή υπαρχόντων, μη διασπασθέντων πυρήνων: ![]() [7.5 ]
[7.5 ]
(Το αρνητικό
πρόσημο σημαίνει, ότι έχουμε ελάττωση του αριθμού των ραδιενεργών
πυρήνων με την πάροδο του χρόνου).
Η σταθερά
αναλογίας λ καλείται σταθερά διασπάσεως και
εξαρτάται μόνο από το είδος του πυρήνα.
Η εξίσωση [ 7.5
] μπορεί να γραφεί και στην μορφή:
![]() [
7.5α ]
[
7.5α ]
Ο ρυθμός των
διασπάσεων (dN/dt) καλείται και ραδιενεργός
δραστηριότητα της συγκεκριμένης ποσότητας του ραδιενεργού
υλικού.
Μονάδα μέτρησης
της ραδιενεργούς δραστηριότητας είναι το Becquerel ![]() .
.
Συχνά
χρησιμοποιείται η ειδική ραδιενεργή
δραστηριότητα ![]() , η οποία μετράται σε Bq/g. Τιμές της ειδικής ραδιενεργής
δραστηριότητας ορισμένων ραδιενεργών ισοτόπων περιέχονται στον Πίνακα
7.5.3.
, η οποία μετράται σε Bq/g. Τιμές της ειδικής ραδιενεργής
δραστηριότητας ορισμένων ραδιενεργών ισοτόπων περιέχονται στον Πίνακα
7.5.3.
|
Πίνακας 7.5.3: Ειδική ραδιενεργή δραστηριότητα μερικών ισοτόπων (Bq/g) |
|||||
|
Μόλυβδος |
|
|
Θόριο |
|
|
|
Βισμούθιο |
|
|
Θόριο |
|
|
|
Πολώνιο |
|
|
Ουράνιο |
|
|
|
Ραδόνιο |
|
|
Ουράνιο |
|
|
|
Ράδιο |
|
|
|
|
|
Ολοκλήρωση της [7.5]
δίδει:
![]()
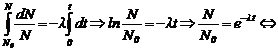
Û ![]() : νόμος της
ραδιενέργειας [7.6]
: νόμος της
ραδιενέργειας [7.6]
|
Σχήμα 7.2: γραφική παράσταση του νόμου της
ραδιενέργειας. |
όπου Ν0 =
αρχικά υπάρχοντες ραδιενεργοί πυρήνες
Η εκθετική ελάττωση
του αριθμού των μη διασπασθέντων πυρήνων με την πάροδο του χρόνου αποδίδεται
ποιοτικά στο σχήμα 7.2.
Ο χρόνος Τ1/2,
εντός του οποίου έχει διασπασθεί το ήμισυ των αρχικώς υπαρχόντων ραδιενεργών πυρήνων,
καλείται χρόνος υποδιπλασιασμού ή ημιζωή. Ο χρόνος
υποδιπλασιασμού μπορεί να υπολογισθεί από την σχέση [7.6] θέτοντας ![]() :
:
![]()
![]()
Þ ![]()
![]()
Þ ![]() : χρόνος
υποδιπλασιασμού [7.7]
: χρόνος
υποδιπλασιασμού [7.7]
Όπως βλέπουμε, ο
χρόνος υποδιπλασιασμού εξαρτάται μόνο από την σταθερή διασπάσεων λ και είναι
κατά συνέπεια χαρακτηριστικός για το συγκεκριμένο ραδιενεργό στοιχείο. Στον
Πίνακα 7.5.3.α δίδεται ο χρόνος υποδιπλασιασμού ορισμένων από τα σπουδαιότερα ραδιενεργά
νουκλίδια.
|
Πίνακας 7.5.3α: Χρόνος υποδιπλασιασμού μερικών
ραδιενεργών νουκλιδίων |
|||||
|
Φώσφορος |
|
14,3 d |
Στρόντιο |
|
29 α |
|
Χλώριο |
|
|
Ράδιο |
|
1601 α |
|
Χλώριο |
|
38 min |
Ουράνιο |
|
|
|
Κάλιο |
|
12,4 h |
Ουράνιο |
|
|
|
Κοβάλτιο |
|
5,25 α |
Ουράνιο |
|
|
|
Στρόντιο |
|
54 d |
Πλουτώνιο |
|
|
6.13 Επίδραση ραδιενεργούς ακτινοβολίας
Τόσο η φυσική
όσο (και κυρίως) η τεχνητή ραδιενέργεια (βλ. κεφ. 7.8) βρίσκουν όλο και περισσότερες
εφαρμογές στην σύγχρονη Ιατρική, Βιολογία και Τεχνολογία γενικότερα. Οι
εν λόγω εφαρμογές αποτελούν αντικείμενο εξειδικευμένων κλάδων των αντιστοίχων
επιστημών και δεν είναι δυνατόν να αναλυθούν στα πλαίσια του παρόντος
συγγράμματος. Εκείνο όμως το οποίο μπορούμε να επισημάνουμε, είναι ότι όλες
αυτές οι εφαρμογές στηρίζονται στις βιολογικές και μη δράσεις της ραδιενεργούς
ακτινοβολίας, τα κύρια γνωρίσματα των οποίων περιγράφουμε παρακάτω.
Βιολογική δράση ραδιενέργειας: Τα σωματίδια αλλά
και τα φωτόνια προκαλούν κατά μήκος της διαδρομής τους τόσο τον ιονισμό ατόμων
όσο και την διάσπαση μορίων. Αυτό έχει ως αποτέλεσμα την πραγματοποίηση
ασυνήθων χημικών αντιδράσεων, οι οποίες πραγματοποιούνται μόνον μεταξύ
ιονισμένων ατόμων. Εξάλλου η διάσπαση ακόμη και μεμονωμένων μορίων επηρεάζει
την λειτουργία των κύτταρων, επειδή αυτή εξαρτάται ακριβώς από την συμπεριφορά
μεμονωμένων μορίων. Έτσι η ραδιενέργεια μπορεί να προκαλέσει την νέκρωση ή
(σχεδόν ακόμη χειρότερα) τον εκφυλισμό των προσβληθέντων κύτταρων. Ένας υγιής
οργανισμός μπορεί φυσικά να αντιμετωπίσει τις παραπάνω βλάβες, μόνον όμως όταν
περιορίζονται σε μερικά μόνο κύτταρα. Σε διαφορετική περίπτωση η ραδιενέργεια
προκαλεί σωματικές και γενετικές βλάβες.
Τις μεγαλύτερες
μεταβολές προξενούν τα σωματίδια α, επειδή προκαλούν - λόγω της μεγάλης τους
μάζας - ιονισμούς κρούσεως ήδη σε πολύ μικρή διαδρομή. Από την άλλη έχουν ως εκ
τούτου μικρή διεισδυτική ικανότητα. Έτσι είναι δραστικά μόνον όταν η πηγή τους
βρεθεί εντός του οργανισμού. Αντιθέτως τα σωματίδια γ χαρακτηρίζονται από μικρή
δραστικότητα μεγάλη όμως διεισδυτικότητα. Το τελευταίο σε συνδυασμό με τις
περιορισμένες δυνατότητες θωράκισης τις κάνει ιδιαίτερα επικίνδυνες. Τα
σωματίδια β έχουν, όσον αφορά την δραστικότητα και διεισδυτικότητα μια
ενδιάμεση θέση.
Μη βιολογική δράση της ραδιενέργειας: Η επίδραση της
ραδιενεργούς ακτινοβολίας επί των διαφόρων υλικών επηρεάζει τις ιδιότητές τους
μέσω δύο κυρίως μηχανισμών. Κατά πρώτον μέσω της διάσπασης μορίων, των οποίων η
επανένωση γίνεται συχνά σε διαφορετική διάταξη από πριν. Αυτό έχει ως
αποτέλεσμα την διαφοροποίηση των φυσικών κυρίως ιδιοτήτων του συγκεκριμένου
υλικού. Η αναδιάταξη αυτή των μορίων έχει μεγαλύτερη επίδραση στην περίπτωση
υλικών, τα οποία αποτελούνται από μακρομόρια. Έτσι πολλά πλαστικά μπορούν μέσω
της ραδιενέργειας να αποκτήσουν π.χ. μεγαλύτερη θερμοκρασιακή αντοχή.
Η έκθεση εξάλλου
ενός υλικού με κρυσταλλική δομή σε σωματίδια υψηλής ενέργειας μπορεί να
προκαλέσει εκσφενδονισμό μεμονωμένων ιόντων του κρυσταλλικού πλέγματος. Αυτό
έχει ως αποτέλεσμα την αλλαγή των ιδιοτήτων του κρυστάλλου, όπως π.χ. την
διαύγεια του, το χρώμα του, την ηλεκτρική του αγωγιμότητα κ.λ.π.
Υπάρχουν βέβαια
και υλικά (όπως τα μέταλλα και τα κεραμικά), τα οποία είναι εξαιρετικά ανθεκτικά
στην έκθεση σε ραδιενεργή ακτινοβολία. Μόνον πάρα πολύ έντονη και μακροχρόνια
έκθεση μπορεί να μεταβάλλει, αισθητά τις ιδιότητές τους.
6.14 Δοσιμετρία
Προκειμένου να
αξιολογήσουμε την επίδραση ραδιενεργούς ακτινοβολίας (γενικότερα κάθε ιονίζουσας
ακτινοβολίας, όπως π.χ. ακτίνες Röntgen, ακτίνες ουδετερονίων κ.λ.π.) επί των διαφόρων υλικών
εισάγουμε την δόση ενέργειας D και τον ρυθμό δόσεως![]() :
:
Απορροφηθείσα
δόση ενέργειας (ή ακτινοβολίας) καλείται το πηλίκο της απορροφηθείσας
από ένα υλικό ενέργειας Ε προς την μάζα m του υλικού:
![]() [7.8]
[7.8]
Μονάδα μέτρησης:
![]() [3]
[3]
Ρυθμός δόσεως ![]() καλείται το πηλίκο
της δόσεως προς τον χρόνο απορρόφησής της:
καλείται το πηλίκο
της δόσεως προς τον χρόνο απορρόφησής της:
![]() [7.9]
[7.9]
Όσον αφορά την
βιολογική δράση της ραδιενεργούς ακτινοβολίας, θα πρέπει να σημειώσουμε, ότι δεν
περιγράφεται πλήρως μέσω της δόσεως, επειδή εξαρτάται και από το είδος της
ακτινοβολίας. Για τον λόγο αυτό εισήχθη η ισοδύναμη ή βιολογικά ισοδύναμη
δόση Dβ ως μέτρο της δράσης
της ακτινοβολίας επί του ανθρωπίνου οργανισμού. Η βιολογική δόση υπολογίζεται
πολλαπλασιάζοντας την δόση D με τον χαρακτηριστικό για το είδος της ακτινοβολίας «παράγοντα ποιότητας» Q:
![]() [
7.10 ]
[
7.10 ]
Η μονάδα
μέτρησης της βιολογικής δόσης ονομάζεται “Sievert” (Sv)[4].
Ο παράγοντας
ποιότητος είναι ουσιαστικά αδιάστατο μέγεθος, το οποίο υπολογίζεται πειραματικά,
συγκρίνοντας το βιολογικό αποτέλεσμα της απορροφηθείσας δόσης ενός συγκεκριμένου
είδους ακτινοβολίας με εκείνο, το οποίο επιφέρει δόση 0,01Gy ακτινών Röntgen. Αυτό σημαίνει
ουσιαστικά, ότι η βιολογική δόση Dβ δεν αποτελεί γνήσιο φυσικό μέγεθος. Στον Πίνακα 7.7 δίδεται ο
παράγοντας ποιότητας ορισμένων ειδών ακτινοβολίας.
|
Πίνακας 7.7: Τιμή του παράγοντα ποιότητας
ορισμένων ακτινοβολιών σε «Sv/Gy» |
|||
|
Ακτίνες
Röntgen |
1 |
Αργά
ουδετερόνια |
3 |
|
»
γ |
1 |
γρήγορα
ουδετερόνια |
10 |
|
»
β |
1 |
γρήγορα
πρωτόνια |
10 |
|
»
α |
10 ~20 |
βαρέα
πυρηνικά θραύσματα |
20 |
Στις σύγχρονες
κοινωνίες έχουν θεσπισθεί ως ανώτατο όριο βιολογικής δόσης τα 50
mSv/α με την
προϋπόθεση, ότι δεν θα ξεπεραστούν τα 30 mSv/(13 εβδομάδες) και τα 50 ·
(ηλικία σε έτη - 18)mSv για όλη την διάρκεια της ζωής. Σημειωτέον δε ότι οι
τιμές αυτές ισχύουν για άτομα, τα οποία έχουν επαγγελματική επιβάρυνση
και υπόκεινται σε προσωπική μέτρηση δόσεως. Για άτομα, τα οποία εκτίθενται ευκαιριακά σε ακτινοβολία, τα ισχύοντα
όρια είναι το 1/10 των παραπάνω, για μεγάλες δε μάζες πληθυσμού το 1/100.
Στον Πίνακα 7.7α περιέχεται, η φυσιολογική δράση διαφόρων βιολογικών δόσεων
ακτινών γ.
|
Πίνακας 7.7α: Βιολογική δράση ακτίνων γ |
|
|
Απορροφηθείσα δόση |
Δράση |
|
< 0,5 Sv |
Μικρή
προσωρινή αλλαγή δεικτών αίματος |
|
0,8 ~ 1,20 Sv |
Αδιαθεσία
και εμετοί στο 10% των περιπτώσεων |
|
4 ~ 5 Sv |
Θάνατοι
σε ποσοστό 50% εντός 30 ημερών. Όσοι επιζήσουν συνέρχονται εντός 6 μηνών. |
|
5,5 ~ 7,5 Sv |
Θάνατοι σε
ποσοστό 100% |
|
50 Sv |
Βαριά
προσβολή του νευρικού συστήματος. Θάνατος εντός μιας βδομάδας |
6.15 Τεχνητή ραδιενέργεια. Σχάση
Ακόμη και
ευσταθείς πυρήνες είναι δυνατόν να μετατραπούν σε ραδιενεργούς, αν τους «βομβαρδίσουμε»
με κατάλληλα «βλήματα», όπως πρωτόνια, ουδετερόνια και σωματίδια α. Η κατ'
αυτόν τον τρόπο εκπεμπόμενη ραδιενέργεια καλείται τεχνητή ραδιενέργεια
και αποτελείται από τα ίδια σωματίδια με την φυσική ραδιενέργεια. Φυσική
και τεχνητή ραδιενέργεια είναι ως εκ τούτου το ίδιο επικίνδυνες για τους
ζώντες οργανισμούς.
Από όλες τις
δυνατότητες τεχνητής διάσπασης ενός αρχικά ευσταθούς πυρήνα ιδιαίτερο πρακτικό
ενδιαφέρον έχει η από τους Hahn και Strassmann το 1938 ανακαληφθείσα και ως σχάση
χαρακτηριζόμενη. Πρόκειται για την διάσπαση ενός (βαρέως) πυρήνα σε δύο περίπου
ισόμαζα θραύσματα, και όχι απλώς την εκπομπή μεμονωμένων σωματιδίων α, β, γ, p, n κ.λ.π.
Σημειωτέον ότι λίγοι μόνον από τους υπάρχοντες στην φύση πυρήνες μπορούν να
υποστούν σχάση. Ο γνωστότερος όλων εκείνος του Ουρανίου ![]() . Η σχάση του εν λόγω πυρήνα επιτυγχάνεται μέσω
βομβαρδισμού με «αργά» (βλ. παρακάτω) ουδετερόνια και εξελίσσεται ποικιλοτρόπως.
Η παρακάτω πυρηνική αντίδραση περιγράφει δύο από τις πολλές δυνατότητες:
. Η σχάση του εν λόγω πυρήνα επιτυγχάνεται μέσω
βομβαρδισμού με «αργά» (βλ. παρακάτω) ουδετερόνια και εξελίσσεται ποικιλοτρόπως.
Η παρακάτω πυρηνική αντίδραση περιγράφει δύο από τις πολλές δυνατότητες:
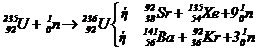
Κατά την σχάση
ενός πυρήνα εκλύεται μεγάλη ποσότητα ενέργειας, η οποία καλείται πυρηνική
ενέργεια και οφείλεται στο έλλειμμα μάζας: το άθροισμα των μαζών των
θραυσμάτων και των εκπεμπομένων σωματιδίων είναι μικρότερο από την μάζα του
αρχικού πυρήνα και των χρησιμοποιηθέντων βλημάτων. Π.χ. στην παραπάνω περίπτωση
του Ουρανίου το έλλειμμα μάζας ανέρχεται σε 1% περίπου. Έτσι 1 kg Ουρανίου δίδει
περίπου 7·1013 J, εκ των οποίων το 83% παραλαμβάνεται ως κινητική
ενέργεια των θραυσμάτων, το 3% ως κινητική ενέργεια των ουδετερονίων και το 3%
εκπέμπεται με μορφή ακτινοβολίας (όλα τα %% στο περίπου).
Τα κατά την
σχάση παραγόμενα δευτερογενή, όπως λέγονται, ουδετερόνια μπορούν
να χρησιμοποιηθούν για την επίτευξη άλλων σχάσεων, αφού προηγουμένως επιβραδυνθούν
σε «θερμικές» (βλ. παρακάτω) ταχύτητες. Εφόσον δε διαθέτουμε μια ελάχιστη,
«κρίσιμη» ποσότητα σχάσιμου υλικού, έχουμε μια αυτοσυντηρούμενη, αλυσιδωτή αντίδραση.
Η αλυσιδωτή
αντίδραση μπορεί να είναι μη ελεγχόμενη, όπως π.χ. στην περίπτωση της
ατομικής βόμβας: Το σχάσιμο υλικό ![]() ή (Πλουτώνιο)
ή (Πλουτώνιο) ![]() είναι αρχικά
χωρισμένο σε αρκετές υποκρίσιμες ποσότητες. Όταν θέλουμε να εκραγεί φέρουμε τις
ποσότητες αυτές σε επαφή με την βοήθεια κατάλληλα τοποθετημένων χημικών
εκρηκτικών. Έτσι η μάζα γίνεται υπερκρίσιμη και αρχίζει η αλυσιδωτή αντίδραση,
ενώ τα ανθεκτικά τοιχώματα του περιβλήματος εμποδίζουν την εκτόξευση σχάσιμου
υλικού πριν την «καύση» του.
είναι αρχικά
χωρισμένο σε αρκετές υποκρίσιμες ποσότητες. Όταν θέλουμε να εκραγεί φέρουμε τις
ποσότητες αυτές σε επαφή με την βοήθεια κατάλληλα τοποθετημένων χημικών
εκρηκτικών. Έτσι η μάζα γίνεται υπερκρίσιμη και αρχίζει η αλυσιδωτή αντίδραση,
ενώ τα ανθεκτικά τοιχώματα του περιβλήματος εμποδίζουν την εκτόξευση σχάσιμου
υλικού πριν την «καύση» του.
Αντιθέτως εις
τους λεγόμενους πυρηνικούς αντιδραστήρες μπορούμε με διάφορα
απλά, μηχανικά μέσα να ελέγχουμε την ταχύτητα μιας αλυσιδωτής αντίδρασης,
επιτυγχάνοντας έτσι την αξιοποίηση της πυρηνικής ενέργειας για την παραγωγή
ισχύος.
Ένας τυπικός
πυρηνικός αντιδραστήρας αποτελείται ουσιαστικά από τα ακόλουθα συστήματα:
1.
Σχάσιμο υλικό («καύσιμο»): Συνήθως
πρόκειται για εμπλουτισμένο Ουράνιο, δηλαδή μείγμα ![]() (χρόνος
υποδιπλασιασμού
(χρόνος
υποδιπλασιασμού ![]() ) και
) και ![]()
![]() , στο οποίο το σχάσιμο
, στο οποίο το σχάσιμο ![]() περιέχεσαι σε
αναλογία μεγαλύτερη εκείνης (0,7%), με την οποία απαντάται στην φύση. Το σχάσιμο
υλικό περιέχεται συνήθως με την μορφή ράβδων, οι οποίες αποτελούνται από μεμονωμένα
δισκία εμπλουτισμένου ουρανίου.
περιέχεσαι σε
αναλογία μεγαλύτερη εκείνης (0,7%), με την οποία απαντάται στην φύση. Το σχάσιμο
υλικό περιέχεται συνήθως με την μορφή ράβδων, οι οποίες αποτελούνται από μεμονωμένα
δισκία εμπλουτισμένου ουρανίου.
2.
Επιβραδυντής: Τα εκπεμπόμενα κατά την σχάση,
δευτερογενή ουδετερόνια πρέπει να επιβραδυνθούν το ταχύτερο δυνατό σε ταχύτητες
της τάξεως 2000 m/s («θερμικά
ουδετερόνια»). Διαφορετικά δεν προκαλούν σχάση άλλων πυρήνων ![]() , αλλά παγιδεύονται από μη σχάσιμους πυρήνες
, αλλά παγιδεύονται από μη σχάσιμους πυρήνες ![]() . Η εν λόγω επιβράδυνση γίνεται μέσω ελαστικής κρούσεως
με πυρήνες μιας ουσίας, του επιβραδυντού, εντός του οποίου είναι
«βυθισμένοι» οι ράβδοι Ουρανίου. Οι πυρήνες του επιβραδυντού πρέπει να είναι
ελαφροί και να μην απορροφούν ουδετερόνια. Τις ιδιότητες αυτές έχουν το βαρύ ή
σύνηθες ύδωρ καθώς και ο καθαρός Άνθρακας με την μορφή Γραφίτη.
. Η εν λόγω επιβράδυνση γίνεται μέσω ελαστικής κρούσεως
με πυρήνες μιας ουσίας, του επιβραδυντού, εντός του οποίου είναι
«βυθισμένοι» οι ράβδοι Ουρανίου. Οι πυρήνες του επιβραδυντού πρέπει να είναι
ελαφροί και να μην απορροφούν ουδετερόνια. Τις ιδιότητες αυτές έχουν το βαρύ ή
σύνηθες ύδωρ καθώς και ο καθαρός Άνθρακας με την μορφή Γραφίτη.
3.
Ράβδοι ρύθμισης: Η ισχύς του
αντιδραστήρα μπορεί να αυξομειωθεί με την βοήθεια ράβδων ή πλακών από Κάδμιο ή
Βάριο, οι οποίες παρεμβάλλονται μεταξύ των ράβδων Ουρανίου και απορροφούν μέρος
των δευτερογενών ουδετερονίων.
4.
Ψυκτικό ρευστό: Η εκλυόμενη
κατά την πυρηνική σχάση ενέργεια (ένα γραμμάριο φυσικού Ουρανίου παράγει τόση
ενέργεια, όση περίπου και 125 τόνοι Άνθρακα!) αποδίδεται αρχικά, κυρίως ως
κινητική ενέργεια των θραυσμάτων. Μέσω κρούσεων αυτών με το περιβάλλον
μετατρέπεται στην συνέχεια σε θερμότητα, η οποία απάγεται με την βοήθεια
καταλλήλου ψυκτικού ρευστού. Τέτοιο μπορεί να είναι για παράδειγμα σύνηθες ή
βαρύ ύδωρ, το οποίο μπορεί να παίζει συγχρόνως και τον ρόλο του επιβραδυντού.
Το ψυκτικό ρευστό αποδίδει την θερμότητα αυτή σε κατάλληλους εναλλάκτες,
προκειμένου να μετατραπεί με την βοήθεια ατμοστροβίλων σε ηλεκτρική ενέργεια.
Προβληματισμοί
Η μέσω πυρηνικών
αντιδραστήρων ειρηνική αξιοποίηση της πυρηνικής ενέργειας περιήλθε (κυρίως μετά
το ατύχημα του Τσερνομπίλ) τα τελευταία χρόνια σε κατάσταση έντονης
αμφισβήτησης, λόγω των προβλημάτων τα οποία μπορεί να προκαλέσει σε περίπτωση
ατυχήματος ή κακού σχεδιασμού.
Συγκεκριμένα,
όλοι οι κατά την σχάση παραγόμενοι πυρήνες είναι ραδιενεργοί και εκπέμπουν
ακτινοβολία β και γ. Το 10% περίπου της εκλυόμενης ενέργειας απάγεται μέσω της
εν λόγω ακτινοβολίας. Το γεγονός αυτό σε συνδυασμό με την μεγάλη εμβέλεια και
καταστροφική δράση κυρίως των ακτινών γ επιβάλλει την λήψη πολυδάπανων (και ως
εκ τούτου στις πρώην «ανατολικές» κυρίως χώρες ανύπαρκτων) και πολύπλοκων
προστατευτικών μέσων.
Ραδιενεργά
καθίστανται εξάλλου και όλα τα εντός της «ψυχής» του αντιδραστήρα ευρισκόμενα
υλικά (π.χ. το ψυκτικό ρευστό, οι ράβδοι του σχάσιμου υλικού, ο επιβραδυντής,
τα υλικά των τοιχωμάτων κ.λ.π.), τα οποία δεν επιτρέπεται ως εκ τούτου να
έλθουν σε επαφή με το περιβάλλον. Κάτι τέτοιο δεν μπορεί όμως να αποκλεισθεί
λόγω της πάντα υπαρκτής πιθανότητας ατυχήματος, όπως δυστυχώς είδαμε και στην
πραγματικότητα. Άλλωστε και υπό ομαλές συνθήκες λειτουργίας σοβαρότατο
παραμένει το πρόβλημα της ασφαλούς αποθήκευσης των ραδιενεργών αποβλήτων,
των «κομμένων» δηλαδή ράβδων ουρανίου.
Αν κάποιος τώρα
πάρει υπόψη του το γεγονός, ότι τα σχάσιμα υλικά είναι στην φύση σχετικά
σπάνια, τότε αντιλαμβάνεται ότι η πυρηνική ενέργεια δεν μπορεί να παίξει τον
ρόλο που θέλουν να τις δώσουν κάποιες χώρες, απλώς και μόνο για να σκεπάσουν
από την παγκόσμια κοινή γνώμη τον ουσιαστικό σκοπό λειτουργίας των
αντιδραστήρων: την παραγωγή
πλουτωνίου,
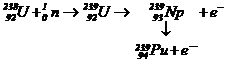 , υλικού απαραίτητου για την κατασκευή πυρηνικών
βομβών!
, υλικού απαραίτητου για την κατασκευή πυρηνικών
βομβών!
ΒΙΒΛΙΟΓΡΑΦΙΑ
1.
2.
Βουδούρης Γ. : Ηλεκτροτεχνία, Έκδοση 3η ,
Αθήνα 1959
3.
Dobrinski/Krakau/Vogel: Physic für
Ingenieure, Έκδοση 4η,
Teubner Stuttgar, 1976
4. Feynman, Eighton, Sands:
The Feynman Lectures of Physics, Volume ll, Έκδοση 16η ,
5.
Gerthsen- Kneser- Vogel: PHYSIK, Έκδοση 13η,
Springer- Verlag, Berlin, 1977.
6.
Halliday- Resnick: ΦΥΣΙΚΗ (Μέρος Β), Εκδόσεις Γ.Α.Πνευματικός, Αθήνα 1976.
7.
Hering, Martin, Stohrer, Physik für
Ingenieure, Έκδοση 5η, VDI
Verlag, 1995.
8.
Jackson J.D.: Klassische Elektrodynamik,
Έκδοση 2η, de
Gruyter, Berlin, 1983.
9.
Kittel Ch.: Einführung in die
Festkörperphysik, Έκδοση 5η, Oldenburg Verlag,
München, 1980.
10. Kuchling,
Taschenbuch der Physik, Verlag Harri Deutsch, Thun 1979
11. Wagner
M.: Elemente der Theoretischen Physik 2, rororo vieweg Physik, 1977.
[1]( Αγωγοί πρώτης τάξεως: η διέλευση του ηλεκτρικού ρεύματος δεν συνοδεύεται από μεταφορά μάζας. Π.χ. μεταλλικοί αγωγοί. Αγωγοί δευτέρας τάξεως: η διέλευση του ηλ. ρεύματος συνοδεύεται από μεταφορά μάζας. Π.χ. Ηλεκτρολύτες.)
[2] Οι «περίεργοι» δεκαδικοί αριθμοί προκύπτουν επειδή εννοείταιη μέση τιμή για όλα τα ισότοπα ενός στοιχείου, λαμβανομένης υπόψη της συχνότητας με την οποία συναντώνται στην φύση.
[3] Παλαιότερα χρησιμοποιούνταν το rad: 1Gy = 100 rad.
[4] Παλαιότερα χρησιμοποιούνταν το rem: 1 Sv = 100 rem.