ΚΕΦΑΛΑΙΟ 1

ΕΙΣΑΓΩΓΗ

Γραμμικός Προγραμματισμός είναι η διαδικασία εύρεσης μιας βέλτιστης λύσης μιας γραμμικής συνάρτησης, η οποία να είναι συμβατή με ένα πεπερασμένο σύνολο γραμμικών ανισοτήτων, δηλαδή, ο γραμμικός προγραμματισμός περιγράφει ένα μοντέλο που αφορά τη μεγιστοποίηση ή ελαχιστοποίηση μιας γραμμικής συνάρτησης κάτω από κάποιους γραμμικούς περιορισμούς. Από την οικονομική σκοπιά, ο γραμμικός προγραμματισμός είναι μια τεχνική που ασχολείται με το πρόβλημα της κατανομής των περιορισμένων πόρων ενός συστήματος σε ανταγωνιζόμενες δραστηριότητες κατά τον καλύτερο δυνατό τρόπο (καθώς και με άλλα προβλήματα με ανάλογη ή παραπλήσια διαμόρφωση). Θεωρείται σαν μια από τις πιο σπουδαίες μαθηματικές ανακαλύψεις των μέσων χρόνων του εικοστού αιώνα και στις μέρες μας αποτελεί ένα μοντέλο ευρείας χρήσης για καθημερινά ζητήματα των περισσότερων μεσαίου και μεγάλου μεγέθους εμπορικών - βιομηχανικών εταιρειών. Ο όρος «προγραμματισμός» δεν έχει την έννοια του «προγραμματισμού ηλεκτρονικών υπολογιστών» αλλά αυτήν του «σχεδιασμού». Ο γραμμικός προγραμματισμός ασχολείται με τη σχεδίαση των δραστηριοτήτων του συστήματος που περιγράφει για να προκύψει το άριστο αποτέλεσμα, το αποτέλεσμα δηλαδή εκείνο, που μεταξύ όλων των δυνατών εναλλακτικών λύσεων πραγματώνει τον προκαθορισμένο σκοπό κατά τον καλύτερο δυνατό τρόπο. Ο γραμμικός προγραμματισμός παρουσιάζει, επίσης, ιδιαίτερο ενδιαφέρον για τη θεωρητική πληροφορική. Μπορεί να χρησιμοποιηθεί για τη μοντελοποίηση και την επίλυση πολλών συνδυαστικών προβλημάτων τα οποία εκ πρώτης όψεως δεν σχετίζονται με το γραμμικό προγραμματισμό. Έτσι, ο ελλειψοειδής αλγόριθμος (ο πρώτος αλγόριθμος πολυωνυμικού χρόνου για το γραμμικό προγραμματισμό) ή οι πιο πρόσφατες μέθοδοι των εσωτερικών σημείων μπορούν να χρησιμοποιηθούν για την αποδοτική επίλυση πολλών συνδυαστικών προβλημάτων, όπως για παράδειγμα ο υπολογισμός βέλτιστων ροών σε ένα δίκτυο, η εύρεση ενός μέγιστου ταιριάσματος (maximal matching) σε ένα γράφο, ή ενός χρωματισμού σε ένα τέλειο γράφημα. Η αρχική μαθηματική διατύπωση του προβλήματος καθώς και μια συστηματική διαδικασία λύσης του, η μέθοδος Simplex, οφείλεται στον G. B. Dantzig στα 1947. Νωρίτερα διάφορα προβλήματα τύπου γραμμικού προγραμματισμού είχαν διαμορφωθεί και επιλυθεί. Τα σημαντικότερα από αυτά αφορούν το πρόβλημα μεταφοράς (Hitchcock 1941, Koopmans 1949) και το πρόβλημα της δίαιτας (Stigler 1945). Ο Dantzig ήταν όμως ο άνθρωπος που κατασκεύασε το γενικό πλαίσιο και ταυτόχρονα ανακάλυψε μέθοδο επίλυσης του.

Πολλά από τα προβλήματα που έχουμε να αντιμετωπίσουμε ανάγονται σε γραμμικά προβλήματα. Κλασικά παραδείγματα αποτελούν τα προβλήματα προγραμματισμού των πληρωμάτων σε μια αεροπορική εταιρία, ο υπολογισμός του συνδυασμού πρώτων υλών σε ένα εργοστάσιο που μεγιστοποιεί το κέρδος του τελικού προϊόντος, ή ο υπολογισμός των ροών αυτοκινήτων σε ένα οδικό δίκτυο, ή του φόρτου πληροφοριών σε ένα δίκτυο επικοινωνίας.

1.1 ΙΣΤΟΡΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ

Ο Γραμμικός Προγραμματισμός είναι μια πολύ σημαντική κλάση προβλημάτων, τόσο από αλγοριθμική, όσο και από συνδυαστική σκοπιά. Από αλγοριθμική σκοπιά, ο αλγόριθμος Simplex προτάθηκε στη δεκαετία του 1940 (λίγο μετά τον πόλεμο) και, παρά το ότι λειτουργεί πολύ αποδοτικά στην πράξη, είναι γνωστό ότι έχει εκθετικό χρόνο εκτέλεσης στη χειρότερη περίπτωση. Από την άλλη πλευρά, είναι ήδη γνωστό από τις αρχές της δεκαετίας του 1970, όταν οι κλάσεις ορίστηκαν, παρατηρήθηκε ότι ο γραμμικός προγραμματισμός ανήκει στην , παρά το γεγονός ότι κανένας πολυωνυμικού χρόνου αλγόριθμος δεν ήταν γνωστός μέχρι τότε. Ο πρώτος πολυωνυμικού χρόνου αλγόριθμος, ο Ελλειψοειδής, ανακαλύφθηκε στα τέλη της δεκαετίας του 1970. Ο αλγόριθμος του Καρμακαρ που ανακαλύφτηκε στη δεκαετία του 1980, οδήγησε στη συστηματική μελέτη των μεθόδων εσωτερικών σημείων για το γραμμικό προγραμματισμό.

Από συνδυαστικής άποψης, τα συστήματα γραμμικών ανισοτήτων μελετήθηκαν από τους Farkas και Minkovsky από τα τέλη του 19ου αιώνα. Ο γραμμικός προγραμματισμός, και ιδιαίτερα η δυϊκότητα, αποτελούν πολύ ισχυρά αποδεικτικά εργαλεία. Η δύναμη τους αξιοποιήθηκε ιδιαίτερα στους προσεγγιστικούς αλγορίθμους που μελετήθηκαν εκτενώς στη δεκαετία του 1990 και συνεχίζουν να μελετώνται εντατικά και σήμερα. Επίσης στους αλγορίθμους δικτυακών ροών ο γραμμικός προγραμματισμός παίζει πολύ σημαντικό ρόλο, τόσο αλγοριθμικά όσο και από συνδυαστικής απόψεως.

1.2 ΜΟΡΦΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ (Π.Γ.Π.)

Όπως θα δούμε στη συνέχεια, αν κάποιος καταφέρει να προσαρμόσει το πρόβλημα του στο πρότυπο του γραμμικού προγραμματισμού, έχει στη διάθεση του ένα σύνολο εργαλείων, όχι μόνο για να βρει την καλύτερη λύση στο ερώτημα που τον απασχολεί, αλλά και για να προχωρήσει σε μια ανάλυση υποθέσεων για τις διάφορες παραμέτρους του προβλήματος. Εν τούτοις, κι αυτό είναι κάτι που δεν πρέπει ποτέ να ξεχνάμε καθώς βυθιζόμαστε στις λεπτομέρειες της όποιας λύσης, το κύριο μέρος κάθε εφαρμογής της Επιχειρησιακής Έρευνας είναι η μοντελοποίηση. Η λύση, ανεξάρτητα από το πόσο λεπτομερής ή εξεζητημένη είναι, έχει απλά έναν υποστηρικτικό ρόλο.

Το γραμμικό μοντέλο-πρότυπο, σχηματίζεται από τα εξής τρία βασικά συστατικά:

· τις μεταβλητές (αγνώστους) του προβλήματος,

· έναν αντικειμενικό στόχο που θα πρέπει να επιτευχθεί, και

· τους περιορισμούς που θα πρέπει να ενσωματώσουμε στις μεταβλητές ώστε να ικανοποιούνται οι συνθήκες του προβλήματος.

Οι μεταβλητές είναι τα δομικά στοιχεία του προβλήματος που μπορεί να επηρεάσει ο αναλυτής. Για το λόγο αυτό συχνά αναφέρονται και ως μεταβλητές ελέγχου ή μεταβλητές απόφασης. Ας πάρουμε για παράδειγμα μια βιομηχανία γάλακτος που προετοιμάζει την ημερήσια γραμμή παραγωγής της. Πολλές είναι οι μεταβλητές που υπάρχουν σ' ένα τέτοιο πρόβλημα. Μεταξύ τους, εύκολα μπορούμε να αναφέρουμε την ποσότητα των διαφορών τύπου γάλακτος, τυριού και γιαουρτιού που θα παρασκευαστούν:

= η ποσότητα (lit) πλήρους γάλακτος που θα παρασκευαστεί,

= η ποσότητα (lit) άπαχου γάλακτος που θα παρασκευαστεί,

= η ποσότητα (Kg) τυριού φέτας που θα παρασκευαστεί,

=…

…

(χρησιμοποιούμε συνήθως το γράμμα για να παραστήσουμε μια μεταβλητή και με έναν δείκτη επιτυγχάνουμε τη μεταξύ τους διάκριση).

Το πρόβλημα αφορά βέβαια τον εντοπισμό τιμής για την κάθε μεταβλητή απόφασης ώστε να ... Χρειαζόμαστε δηλαδή έναν αντικειμενικό στόχο. Ο στόχος αυτός μπορεί να αφορά τη μεγιστοποίηση του κέρδους, της καλύτερης αξιοποίησης του εργατικού δυναμικού, ή την ελαχιστοποίηση του κόστους, της υπερωριακής απασχόλησης, κτλ. Ψάχνουμε να βρούμε εκείνες τις τιμές των μεταβλητών ελέγχου οι οποίες θα βελτιστοποιήσουν το κριτήριο απόδοσης που ορίζουμε σ' αυτό το στάδιο της μοντελοποίησης. Στο παράδειγμα της γαλακτοβιομηχανίας που αναφέρθηκε πιο πάνω, θα μπορούσαμε να ορίσουμε σαν στόχο την ημερήσια μεγιστοποίηση των κερδών κι επομένως να αναζητήσουμε έναν τρόπο έκφρασης του συνολικού κέρδους σαν συνάρτηση των μεταβλητών απόφασης (προϊόντων που παρασκευάζονται) εκτιμώντας τη συνεισφορά του καθενός χωριστά.

Ο αντικειμενικός στόχος που θα οριστεί θα πρέπει να επιτευχθεί κάτω από τους συνθήκες λειτουργίας του συστήματος που μελετάμε. Περιορισμοί, όπως η ανεπάρκεια των πόρων του συστήματος (π.χ. πρώτων υλών, εργατικού δυναμικού), η απορροφητικότητα της αγοράς, οι συμφωνίες με προμηθευτές και αγοραστές, οι χρόνοι παράδοσης των παραγόμενων προϊόντων, κτλ. δημιουργούν αυτές τις συνθήκες. Αν η προαναφερόμενη βιομηχανία γάλακτος ήταν σε θέση να εξασφαλίσει απεριόριστη πρώτη ύλη και παραγωγική δυναμικότητα καθώς επίσης και μονοπωλιακή παρουσία στην αγορά θα εκτόξευε τα κέρδη της στο άπειρο. Τα πράγματα βέβαια είναι εντελώς διαφορετικά. Στο στάδιο αυτό της μοντελοποίησης, καλούμαστε να εντοπίσουμε και να καταγράψουμε σαν συνάρτηση των μεταβλητών απόφασης τους παράγοντες οι οποίοι επιβάλλουν όρια στις τιμές τους και συνεπώς και στην τιμή της αντικειμενικής συνάρτησης.

Στο πρότυπο του προβλήματος γραμμικού προγραμματισμού τόσο ο αντικειμενικός στόχος, όσο και οι περιορισμοί εκφράζονται σαν γραμμικές συναρτήσεις των μεταβλητών απόφασης.

Παράδειγμα 1.1

Ας δούμε όμως ένα παράδειγμα γραμμικού προγραμματισμού, το κλασικό πλέον πρόβλημα της ΔΙΑΙΤΑΣ . Ας υποθέσουμε ότι ο ελάχιστος αριθμός των θερμίδων που μπορούμε να λαμβάνουμε καθημερινά είναι ορισμένος. Επίσης, σε καθημερινή βάση απαιτείται να προσλαμβάνουμε μια ελάχιστη ποσότητα πρωτεϊνών και ασβεστίου, ενώ παράλληλα επιθυμούμε να δαπανούμε το ελάχιστο δυνατό ποσό κάθε μέρα. Ο πίνακας του σχήματος 1.1 απεικονίζει τις παρεχόμενες πρωτεΐνες και ασβέστιο (σε miligrams ανά μερίδα) που εξασφαλίζει συγκεκριμένη ποσότητα (δηλαδή, η τυπική δοσολογία) κάθε είδους τροφής που έχουμε στη διάθεση μας, καθώς επίσης και τις θερμίδες που περιέχουν.

Είδος τροφής	Δοσολ.	θερμ.(Kcal)	Πρωτ.(gr)	Ασβ.(mg)	Τιμή(ευρώ)
(1) Δημητριακά	28 γρ.	110	4	2	0.3
(2) Κοτόπουλο	100 γρ.	205	32	12	2.4
(3) Αβγά	2	160	13	54	1.3
(4) Γάλα	237κ.ε.	160	8	285	0.9
(5) Γλυκό	170 γρ.	420	4	22	2.0
(6) Χοιρινό	260 γρ.	260	14	80	1.9
Απαιτήσεις		2000	55	800

Σχήμα 1.1: Ο πίνακας με τα στοιχεία του παραδείγματος για το πρόβλημα της Δίαιτας.

Η τελευταία γραμμή του πίνακα απεικονίζει τις καθημερινές μας απαιτήσεις σε θερμίδες, πρωτεΐνες και ασβέστιο. Ας υποθέσουμε ότι από το ί-στό είδος τροφής χρησιμοποιούμε δόσεις (δηλαδή, τόσες φορές επί τη δοσολογία που ορίζει ο πίνακας). Τότε εύκολα εκφράζει κανείς τους περιορισμούς που περιγράφει η τελευταία γραμμή του πίνακα ως εξής:

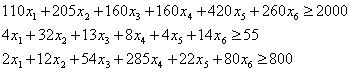
θυμηθείτε όμως ότι επιθυμούμε να πληρώνουμε το ελάχιστο δυνατό ποσό ημερησίως, συνεπώς ο στόχος μας είναι ο εξής:

Φυσικά, δεν είναι δυνατόν να καταναλώνουμε αρνητικές ποσότητες τροφών. Συνολικά, το πρόβλημα της Δίαιτας μπορεί να περιγραφεί φορμαλιστικά όπως φαίνεται στο σχήμα 1.2. Χρησιμοποιώντας μια οποιαδήποτε εφαρμογή για επίλυση γραμμικών προβλημάτων (πχ, Lindo^®) μπορεί κάποιος εύκολα να διαπιστώσει ότι η βέλτιστη λύση του προβλήματος αυτού είναι

, , , .

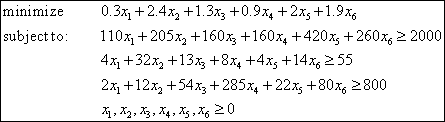
Σχήμα 1.2: Το γραμμικό πρόγραμμα που αναπαριστά το πρόβλημα της Δίαιτας.

Παράδειγμα 1.2

Ας δούμε όμως και ένα δεύτερο παράδειγμα, που σχετίζεται με τη θεωρία γραφημάτων. Έστω ότι μας δίνεται ένας διμερής γράφος (δηλαδή, δυο πεπερασμένα σύνολα κορυφών και ένα σύνολο ακμών .

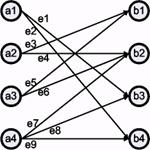
Σχήμα 1.3: Παράδειγμα ενός διμερή γράφου.

Για παράδειγμα, στο σχήμα 1.3 δίνεται ένας διμερής γράφος. Ένα ταίριασμα σε ένα γράφο είναι ένα υποσύνολο των ακμών του τέτοιο ώστε να μην υπάρχει ζευγάρι ακμών στο που να μοιράζονται κάποια κορυφή. Στο παράδειγμα μας το σύνολο ακμών είναι ένα ταίριασμα. Ένα μέγιστο ταίριασμα είναι εκείνο το ταίριασμα που περιλαμβάνει το μεγαλύτερο αριθμό ακμών στο γράφημα. Στο παράδειγμα μας, το ταίριασμα που προαναφέραμε δεν είναι μέγιστο αφού το ταίριασμα έχει μεγαλύτερο πληθαριθμό. Ένα κλασικό ερώτημα είναι πώς μπορεί κανείς να κατασκευάσει ένα μέγιστο ταίριασμα ενός διμερή γράφου.

Κατ' αρχήν θεωρούμε ότι κάθε λύση που παράγουμε (δηλαδή, οποιοδήποτε ταίριασμα) αναπαριστάται από ένα σύνολο ενδεικτικών μεταβλητών, μια για κάθε ακμή του γράφου: . Από αυτό εύκολα συνάγει κανείς ότι θα πρέπει οι μεταβλητές που χρησιμοποιούμε να παίρνουν μη αρνητικές τιμές. Ποιοι είναι όμως οι σωστοί περιορισμοί που μας εξασφαλίζουν ότι ένα υποσύνολο ακμών που επιλέγουμε είναι ταίριασμα του γράφου; Παρατηρείστε ότι η ικανή και αναγκαία συνθήκη είναι ότι οποιαδήποτε κορυφή είναι το άκρο το πολύ μιας ακμής του . Άρα λοιπόν χρειαζόμαστε ένα περιορισμό για κάθε κορυφή που να φράζει με το 1 τον αριθμό των ακμών που την αγγίζουν. Στο παράδειγμα μας, για την κορυφή ο αντίστοιχος περιορισμός είναι ο εξής: , ενώ για την κορυφή είναι . Όλοι αυτοί οι περιορισμοί είναι γραμμικοί ως προς τις μεταβλητές που χρησιμοποιούμε για να αποτυπώσουμε τη λύση που παράγουμε.

Σχήμα 1.4: Το (ακέραιο) γραμμικό πρόγραμμα που αναπαριστά το πρόβλημα του ταιριάσματος για το παράδειγμα μας.

Στόχος μας τέλος είναι η επιλογή εκείνου του συνόλου που θα είναι ταίριασμα (αυτό εξασφαλίζεται από τους περιορισμούς) και θα έχει το μέγιστο δυνατό αριθμό ακμών. Δηλαδή, θέλουμε να μεγιστοποιήσουμε τη συνάρτηση η οποία είναι επίσης γραμμική ως προς τις μεταβλητές του προβλήματος. Στο σχήμα 1.4 φαίνεται το γραμμικό πρόβλημα που περιγράφει το παράδειγμα μας. Το συγκεκριμένο γραμμικό πρόβλημα έχει την ιδιαιτερότητα ότι οι τιμές των μεταβλητών του θα πρέπει να είναι ακέραιοι αριθμοί (για την ακρίβεια, 0 ή 1). Τέτοιου είδους γραμμικά προβλήματα ονομάζονται ακέραια γραμμικά προβλήματα. Εμείς δε μπορούμε να επιλύσουμε αποδοτικά (δηλαδή, σε πολυωνυμικό χρόνο) ένα ακέραιο γραμμικό πρόβλημα, μπορούμε όμως να επιλύσουμε ένα παρόμοιο πρόβλημα, το οποίο φαίνεται στο σχήμα 1.5.

Έστω ότι μπορούμε να κατασκευάσουμε σε πολυωνυμικό χρόνο τη βέλτιστη λύση για το γραμμικό πρόβλημα που αντιστοιχεί στο πρόβλημα του ταιριάσματος σε διμερή γράφο. Γενικά τίποτε δε μας εγγυάται ότι η βέλτιστη λύση ενός γραμμικού προβλήματος θα έχει ακέραιες τιμές στις μεταβλητές απόφασης που χρησιμοποιούμε. Στην περίπτωση του μέγιστου ταιριάσματος σε διμερή γραφήματα γνωρίζουμε όμως ότι υπάρχει πάντοτε μια βέλτιστη λύση που αναθέτει τιμές 0 ή 1 στις ενδεικτικές μεταβλητές που χρησιμοποιούμε για τις ακμές του γράφου. Συνεπώς, θα μπορούσαμε ενδεχομένως να εξασφαλίσουμε την εύρεση της βέλτιστης ακέραιας λύσης χωρίς επιπλέον κόπο. Φυσικά θα πρέπει με κάποιο τρόπο να εξασφαλίσει κανείς ότι η επιστρεφόμενη βέλτιστη λύση είναι και ακέραια, ή να κατασκευάσει (αν είναι δυνατόν) μια βέλτιστη ακέραια λύση με την ίδια τιμή της συνάρτησης-στόχου.

Σχήμα 1.5: Το χαλαρωμένο γραμμικό πρόγραμμα που αναπαριστά το πρόβλημα του ταιριάσματος για το παράδειγμα μας.

Παράδειγμα 1.3

Το πρόβλημα μεταφοράς είναι ένα από τα πρώτα είδη προβλημάτων που αναλύθηκαν με την χρήση του γραμμικού προγραμματισμού. Το γενικό πρόβλημα εμφανίστηκε όταν τα διαθέσιμα αγαθά αποθηκευμένα σε διάφορες πηγές έπρεπε να διανεμηθούν σε ποικίλους προορισμούς. Το πρόβλημα είναι να βρούμε τον βέλτιστο τρόπο μεταφοράς έτσι ώστε να ελαχιστοποιείται το κόστος μεταφοράς. Συγκεκριμένα, διαθέτουμε ποσότητες ενός ομοιόμορφου προϊόντος σε έναν αριθμό αποθηκών και θέλουμε να μεταφέρουμε καθορισμένες ποσότητες του προϊόντος σε έναν αριθμό από διαφορετικούς προορισμούς. Το κόστος για την μεταφορά μιας μονάδας ποσότητας από οποιαδήποτε αποθήκη σε οποιοδήποτε κατάστημα είναι γνωστό, ενώ η μεταφορά από κάθε αποθήκη σε κάθε κατάστημα είναι δυνατή. Θέλουμε να υπολογίσουμε το ελάχιστο κόστος μεταφοράς από τις αποθήκες στα καταστήματα λιανικής πώλησης.

Τρία παραρτήματα ενός εργοστασίου, τα Α, Β, Γ, που παράγουν το ίδιο προϊόν, βρίσκονται σε τρεις διαφορετικές περιοχές της χώρας, που απέχουν πολύ μεταξύ τους. Οι αγοραστές του προϊόντος βρίσκονται σε πέντε διαφορετικές πόλεις. Τα παραρτήματα παράγουν ποσότητες αντίστοιχα 150, 350 και 280 μονάδων του προϊόντος, ενώ οι αγοραστές έχουν παραγγείλει αντίστοιχα 100, 130, 160, 210, και 150 μονάδες. Το κόστος μεταφοράς του προϊόντος από τα παραρτήματα Α, Β , Γ δίνεται στον πίνακα:

Παράρτημα	Αγοραστές
	1 2 3 4 5
Α Β Γ	10 22 8 14 9 12 16 26 20 19 18 21 15 11 17

Θέλουμε να υπολογίσουμε τις απαραίτητες ποσότητες (μεταβλητών αποφάσεως) που θα πρέπει να μεταφερθούν από το παράρτημα i στον αγοραστή j ώστε να ελαχιστοποιηθεί το κόστος μεταφοράς. Άγνωστες είναι οι ποσότητες , όπου i είναι τα Α, Β, Γ και j τα 1, 2, 3, 4, 5. Η αντικειμενική συνάρτηση του προβλήματος ( κόστος μεταφοράς), της οποίας αναζητάμε το ελάχιστο, γράφεται

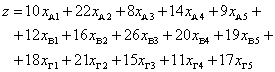
Είναι φανερό ότι δεν μπορούμε να φορτώσουμε περισσότερα προϊόντα από ένα παράρτημα από όσα παράγονται στο παράρτημα αυτό. Συνεπώς έχουμε τους περιορισμούς:

(παραγωγή παραρτήματος Α)

(παραγωγή παραρτήματος Β)

(παραγωγή παραρτήματος Γ)

Επίσης κάθε αγοραστής πρέπει να εφοδιαστεί με τον επιθυμητό αριθμό μονάδων. Συνεπώς έχουμε τους περιορισμούς:

(ζήτηση αγοραστή 1)

(ζήτηση αγοραστή 2)

(ζήτηση αγοραστή 3)

(ζήτηση αγοραστή 4)

(ζήτηση αγοραστή 5)

Επίσης

, με και

1.3 ΟΡΙΣΜΟΙ

Ένα γραμμικό πρόβλημα είναι το πρόβλημα της μεγιστοποίησης μιας γραμμικής συνάρτησης ωφέλειας (ή ελαχιστοποίησης μιας συνάρτησης κόστους), η οποία εξαρτάται από ένα σύνολο μεταβλητών απόφασης , με την προϋπόθεση ότι τηρούνται κάποιοι περιορισμοί ως προς τις τιμές των μεταβλητών αυτών, οι οποίοι εκφράζονται μέσα από ένα σύνολο γραμμικών ισοτήτων και/ή ανισοτήτων. Ο πιο διαδεδομένος τρόπος αναπαράστασης (καλείται γενική μορφή-general form) ενός γραμμικού προβλήματος φαίνεται στο σχήμα 1.6.

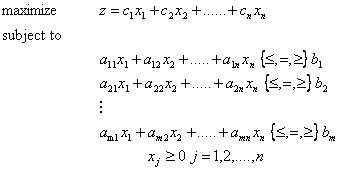
Σχήμα 1.6

Ορισμός 1.1

Μια πραγματική συνάρτηση μεταβλητών

Είναι γραμμική αν και μόνον αν για κάποιο σύνολο πραγματικών σταθερών αριθμών ισχύει:

Ορισμός 1.2

Ένα πρόβλημα βελτιστοποίησης χαρακτηρίζεται σαν πρόβλημα γραμμικού προγραμματισμού (π.γ.π.) όταν

1. Αφορά την μεγιστοποίηση (ή ελαχιστοποίηση) μιας γραμμικής συνάρτησης των αγνώστων (μεταβλητών). Η συνάρτηση αυτή ονομάζεται αντικειμενική συνάρτηση.

2. Οι τιμές των αγνώστων (μεταβλητών) ικανοποιούν ένα σύνολο περιορισμών. Κάθε περιορισμός πρέπει να είναι μια γραμμική εξίσωση ή ανίσωση.

3. Κάθε μεταβλητή είναι μη αρνητική ή δεν έχει περιορισμό στο πρόσημο

Ορισμός 1.3

Κάθε συνδυασμός τιμών των μεταβλητών απόφασης ενός προβλήματος γραμμικού προγραμματισμού ονομάζεται λύση του προβλήματος.

Ορισμός 1.4

Το υποσύνολο του που σχηματίζεται από τα σημεία – λύσεις που ικανοποιούν όλους τους περιορισμούς ενός προβλήματος γραμμικού προγραμματισμού ονομάζεται εφικτή περιοχή του προβλήματος γραμμικού προγραμματισμού, τα δε σημεία εφικτές λύσεις.

Μια λύση, που παραβιάζει τουλάχιστον έναν από τους περιορισμούς, ονομάζεται μη-εφικτή λύση και δεν είναι σημείο της εφικτής περιοχής του προβλήματος γραμμικού προγραμματισμού.

Ορισμός 1.5

Σε ένα πρόβλημα μεγιστοποίησης άριστη ή βέλτιστη λύση ονομάζεται κάθε εφικτή λύση, η οποία μεγιστοποιεί την αντικειμενική συνάρτηση:

.

Όμοια σε ένα πρόβλημα ελαχιστοποίησης θα είχαμε:

.

Ορισμός 1.6

Ένας περιορισμός προβλήματος γραμμικού προγραμματισμού χαρακτηρίζεται σαν δεσμευτικός αν και μόνον αν η άριστη λύση τον καθιστά ισότητα. Στην αντίθετη περίπτωση ονομάζεται χαλαρός.

Το γενικό πρόβλημα γραμμικού προγραμματισμού μπορεί να διατυπωθεί ως εξής:

Να βρεθούν οι τιμές των μεταβλητών που μεγιστοποιούν ή ελαχιστοποιούν την συνάρτηση

Οι μεταβλητές πρέπει να ικανοποιούν τους περιορισμούς

και

όπου τα , , είναι γνωστές σταθερές.

Η συνάρτηση:

ονομάζεται αντικειμενική συνάρτηση (objective function). Αυτή η συνάρτηση είναι γραμμική ως προς τις μεταβλητές . Επίσης, κάθε περιορισμός είναι μια γραμμική συνάρτηση ως προς τις μεταβλητές .

Οι συντελεστές της αντικειμενικής συνάρτησης γενικά αναφέρονται σαν αντικειμενικοί συντελεστές. Σε προβλήματα μεγιστοποίησης χαρακτηρίζονται σαν συντελεστές κέρδους ενώ σε προβλήματα ελαχιστοποίησης σαν συντελεστές κόστους.

Η συνθήκη αναφέρεται και ως συνθήκη της μη αρνητικότητας.

Λύση ενός προβλήματος γραμμικού προγραμματισμού θα ονομάζεται κάθε σύνολο το οποίο ικανοποιεί τους περιορισμούς του προβλήματος.

Εφικτή ή δυνατή λύση είναι κάθε λύση που ικανοποιεί τους περιορισμούς μη αρνητικότητας.

Βέλτιστη λύση είναι κάθε εφικτή λύση η οποία βελτιστοποιεί την αντικειμενική συνάρτηση.

Συνήθως σε ένα πρόβλημα γραμμικού προγραμματισμού υπάρχουν άπειρες λύσεις και επιδιώκουμε την εύρεση της βέλτιστης δυνατής λύσης.

Αν όλοι οι περιορισμοί είναι εξισώσεις ή ανισώσεις της ίδιας φοράς, ένα πρόβλημα γραμμικού προγραμματισμού μπορεί να διατυπωθεί με την χρήση πινάκων ως εξής:

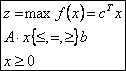
όπου:

, , ,

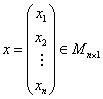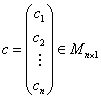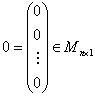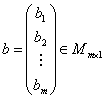
και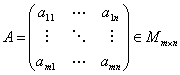

Με παριστάνουμε το διανυσματικό χώρο των πινάκων.

Η σπουδαιότητα της διατύπωσης αυτής έγκειται στο ότι μπορεί με τον παραπάνω τρόπο να διατυπωθεί με σαφήνεια μια μεγάλη ποικιλία οικονομικών, επιστημονικών, βιομηχανικών, επιχειρηματικών και κοινωνικών προβλημάτων.

1.4 ΠΡΟΫΠΟΘΕΣΕΙΣ ΕΦΑΡΜΟΓΗΣ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ

Έχοντας εξετάσει κάποιες περιπτώσεις όπου είναι δυνατό να εφαρμοστεί ο γραμμικός προγραμματισμός και τη γενική διατύπωση ενός προβλήματος γραμμικού προγραμματισμού είναι σημαντικό να εξετάσουμε τις απαιτούμενες προϋποθέσεις για την εφαρμογή του σ’ ένα οποιοδήποτε πρόβλημα βελτιστοποιήσεως. Αυτές είναι που περιορίζουν γενικά το φάσμα των δυνατοτήτων εφαρμογής του γραμμικού προγραμματισμού. Οι προϋποθέσεις που πρέπει να ισχύουν για να διατυπωθεί ένα πρόβλημα γραμμικού προγραμματισμού είναι οι εξής:

α) Γραμμικότητα (Αναλογικότητα και Προσθετικότητα)

β) Διαιρετότητα και

γ) Βεβαιότητα (Προσδιοριστικότητα).

Γραμμικότητα (Αναλογικότητα και Προσθετικότητα)

Όλες οι συναρτήσεις του προβλήματος, αντικειμενική συνάρτηση και περιορισμοί πρέπει να είναι γραμμικές ως προς τις άγνωστες μεταβλητές . Αυτό σημαίνει ότι πρέπει να ισχύουν οι ιδιότητες της αναλογικότητας και της προσθετικότητας, δηλαδή εάν είναι μια συνάρτηση μεταβλητών και είναι σταθερές, πρέπει να ισχύει:

Σε πολλές περιπτώσεις στις οποίες δεν ισχύει απόλυτα η προϋπόθεση της γραμμικότητας μπορεί να γίνει μια αρκετά καλή προσέγγιση με γραμμικές συναρτήσεις.

Διαιρετότητα

Το μοντέλο του γραμμικού προγραμματισμού υποθέτει ότι κάθε δραστηριότητα (δηλ μεταβλητή) είναι συνεχής και επομένως άπειρα διαιρετή. Αυτό συνεπάγεται ότι όλα τα επίπεδα δραστηριοτήτων και όλες οι χρήσεις πόρων επιτρέπεται να πάρουν κλασματικές τιμές ή ακέραιες τιμές. Όταν η υπόθεση της διαιρετότητας δεν ισχύει υπάρχουν δύο ενδεχόμενα :

α) Να αγνοηθεί η υπόθεση αυτή, να λυθεί το πρόβλημα με μεθόδους γραμμικού προγραμματισμού, και οι τιμές των μεταβλητών να στρογγυλευθούν στην κοντινότερη ακέραια μονάδα. Η μέθοδος αυτή εφαρμόζεται κυρίως όταν οι τιμές των μεταβλητών είναι μεγάλες.

β) Όταν οι τιμές των μεταβλητών είναι μικρές (π.χ. 0 ή 1) όπως σε πολλά προβλήματα επενδύσεων τότε πρέπει να χρησιμοποιηθούν τεχνικές του ακέραιου προγραμματισμού.

Βεβαιότητα (Προσδιοριστικότητα)

Το μοντέλο του γραμμικού προγραμματισμού. προϋποθέτει ότι όλοι οι παράμετροι του προβλήματος είναι γνωστές με απόλυτη βεβαιότητα.

Στην περίπτωση που μερικοί ή όλοι οι συντελεστές της αντικειμενικής συνάρτησης ή των περιορισμών είναι τυχαίες μεταβλητές το πρόβλημα γίνεται πρόβλημα στοχαστικού προγραμματισμού.

ΚΕΦΑΛΑΙΟ 2

ΓΡΑΦΙΚΗ ΛΥΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ

Τα προβλήματα γραμμικού προγραμματισμού που έχουν 2 ή 3 μεταβλητές απόφασης, μπορούν να λυθούν και γραφικά. Προβλήματα με δυο μεταβλητές υλοποιούνται στο επίπεδο (δυο διαστάσεις), ενώ προβλήματα με τρεις μεταβλητές υλοποιούνται στον χώρο (τρεις διαστάσεις).

Για να φτάσουμε στην λύση του προβλήματος γραφικά, πρέπει να εκτελέσουμε τα παρακάτω βήματα:

1) σχεδιασμός όλων των περιορισμών γραφικά

2) εύρεση εφικτής περιοχής

3) εύρεση άριστης ή βέλτιστης λύσης

Το τελευταίο βήμα υλοποιείται με δυο τρόπους προσέγγισης της επίλυσης.

Ο πρώτος τρόπος είναι η προσέγγιση της απαρίθμησης και ελέγχου όλων των ακραίων σημείων (κορυφών) της εφικτής περιοχής. Εντοπίζουμε τις συντεταγμένες όλων των κορυφών της εφικτής περιοχής και επιλέγουμε εκείνη που μεγιστοποιεί (ή ελαχιστοποιεί) την αντικειμενική συνάρτηση.

Ο δεύτερος τρόπος είναι η προσέγγιση της χάραξης των καμπύλων ίσου κέρδους (ή κόστους) της αντικειμενικής συνάρτησης. Βρίσκουμε το σημείο όπου η ισοκερδής εφάπτεται της εφικτής περιοχής πριν την εγκαταλείψει.

2.1 ΟΡΙΣΜΟΙ

Περιοριστική ευθεία είναι η ευθεία που αντιστοιχεί σε κάποιο περιορισμό του προβλήματος γραμμικού προγραμματισμού

Κορυφή ή ακραίο σημείο είναι το σημείο που τέμνονται δυο περιοριστικές ευθείες.

Εφικτή περιοχή είναι η κυρτή περιοχή των εφικτών λύσεων που σχηματίζεται από τις περιοριστικές ευθείες.

Εφικτή λύση (ακραίου σημείου) είναι μια κορυφή της εφικτής περιοχής.

Γειτονικές εφικτές λύσεις (ακραίου σημείου) είναι αυτές που συνδέονται με μια ακμή (σύνορο) της εφικτής περιοχής.

Βασική λύση (λύση ακραίου σημείου) είναι μια λύση που αντιστοιχεί σε κορυφή.

Βασική εφικτή λύση είναι μια βασική λύση που αντιστοιχεί σε κορυφή της εφικτής περιοχής.

Άριστη (βέλτιστη) λύση είναι η βασική εφικτή λύση ακραίου σημείου (κορυφή της εφικτής περιοχής) που μας δίνει τη βέλτιστη τιμή στην αντικειμενική συνάρτηση. Δύναται να είναι ακριβώς μια, αλλά υπάρχουν και περιπτώσεις με άπειρες άριστες λύσεις, καμία άριστη λύση, ή η αντικειμενική συνάρτηση να τείνει στο άπειρο.

2.2 ΠΡΟΒΛΗΜΑΤΑ ΜΕΓΙΣΤΟΠΟΙΗΣΗΣ – ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ

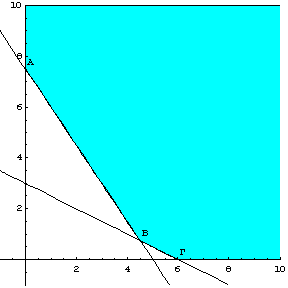
Παράδειγμα 2.1

Γενικό γραμμικό πρόβλημα με πολυγωνική περιοχή εφικτών λύσεων

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

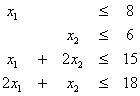
και

Βήμα 1^ο - Γεωμετρική ερμηνεία των περιορισμών του προβλήματος

Α. Εντοπισμός σημείων για τις ευθείες των περιορισμών του π.γ.π.

(1) Η είναι ευθεία παράλληλη στον άξονα της

(2) Η είναι ευθεία παράλληλη στον άξονα της

(3) Για την εξίσωση – ευθεία πρέπει να υπολογίσουμε δύο σημεία που την επαληθεύουν. Για , παίρνουμε , ενώ για , παίρνουμε . Άρα τα σημεία και αρκούν για να σχεδιάσουμε την ευθεία, καθώς από δύο σημεία περνάει μια και μόνο μια ευθεία, όπως προκύπτει από την αναλυτική γεωμετρία.

(4) Για την εξίσωση – ευθεία πρέπει να υπολογίσουμε δύο σημεία που την επαληθεύουν. Για , παίρνουμε , ενώ για , παίρνουμε . Άρα τα σημεία και αρκούν για να σχεδιάσουμε την ευθεία.

Β. Εισαγωγή συστήματος ορθογωνίων συντεταγμένων και σχεδιασμός των περιορισμών (ευθειών).

Μια ευθεία χωρίζει το επίπεδο σε δυο ημιεπίπεδα και η αντίστοιχη γραμμική ανίσωση ορίζει ένα από αυτά τα δυο ημιεπίπεδα. Ένας απλός τρόπος να βρούμε ποιο είναι το ημιεπίπεδο που ορίζει η ανίσωση είναι να επιλέξουμε ένα τυχαίο σημείο (όχι σημείο της ευθείας) το οποίο, αν επαληθεύει την ανίσωση τότε το ημιεπίπεδο που ορίζει η ανίσωση είναι αυτό στο οποίο βρίσκεται το σημείο, διαφορετικά το ημιεπίπεδο που ορίζει η ανίσωση είναι αυτό στο οποίο δεν βρίσκεται το σημείο.

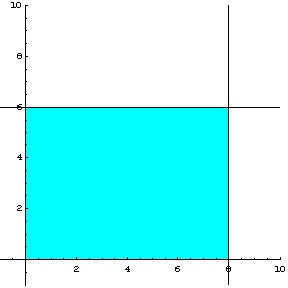
Παρατηρούμε ότι οι περιορισμοί του πρόσημου των μεταβλητών και , ικανοποιούνται μόνο στο πρώτο τεταρτημόριο, και συνεπώς τα ζεύγη τιμών των που αποτελούν δυνατές λύσεις για το πρόβλημα αυτό, θα βρίσκονται σε αυτό το τεταρτημόριο. Στο σχήμα 2.1, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων και , δηλαδή την περιοχή που ορίζουν.

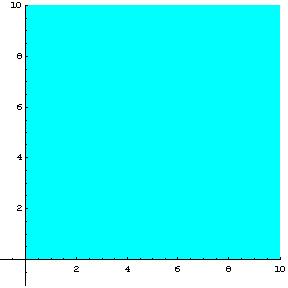
Σχήμα 2.1

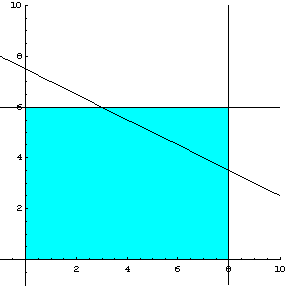
Στο σχήμα 2.2, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , και την ευθεία .

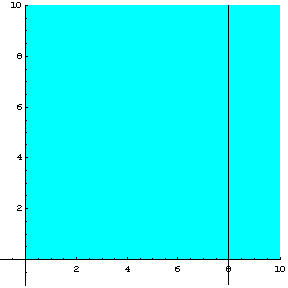
Σχήμα 2.2

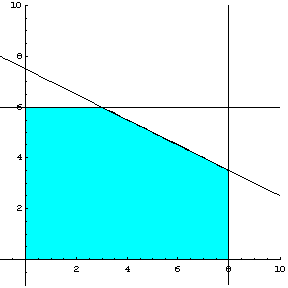
Η ανίσωση επαληθεύεται από το σημείο , επομένως στο σχήμα 2.3, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , και .

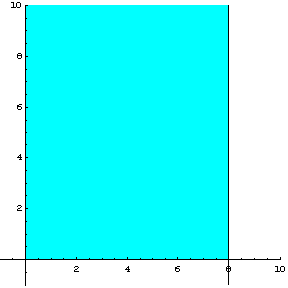
Σχήμα 2.3

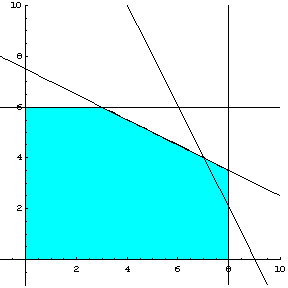
Στο σχήμα 2.4, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , και την ευθεία .

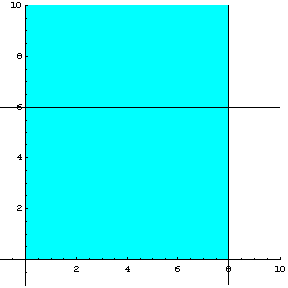
Σχήμα 2.4

Η ανίσωση επαληθεύεται από το σημείο , επομένως στο σχήμα 2.5, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , και .

Σχήμα 2.5

Στο σχήμα 2.6, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , , και την ευθεία .

Σχήμα 2.6

Η ανίσωση επαληθεύεται από το σημείο , επομένως στο σχήμα 2.7, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , , και .

Σχήμα 2.7

Στο σχήμα 2.8, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , , , και την ευθεία .

Σχήμα 2.8

Η ανίσωση επαληθεύεται από το σημείο , επομένως στο σχήμα 2.9, μπορούμε να δούμε τη γεωμετρική ερμηνεία των ανισοτήτων , , , , και , δηλαδή, την εφικτή περιοχή του προβλήματος.

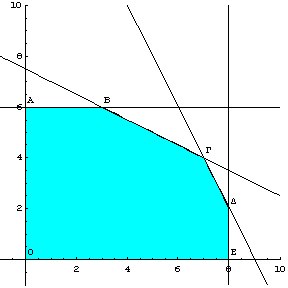
Σχήμα 2.9

Παρατηρούμε λοιπόν, ότι, η ανίσωση ικανοποιείται σε όλα τα σημεία του τεταρτημορίου που βρίσκονται πάνω στην ευθεία και αριστερά από αυτή, ενώ η ανίσωση σε όλα τα σημεία πάνω στην ευθεία και κάτω από αυτή. Για τις ανισότητες και , παρατηρούμε ότι το ζεύγος τιμών , τις ικανοποιεί. Κάθε σημείο κάτω και μόνο κάτω από τις ευθείες και , συμπεριλαμβανομένων των ίδιων των ευθειών, ικανοποιεί και τις ανισότητες και . Στο σχήμα 2.9, μπορούμε να δούμε τα ζεύγη τιμών που ικανοποιούν ταυτόχρονα όλους τους περιορισμούς του προβλήματος (γραμμοσκιασμένη περιοχή - ΟΑΒΓΔΕ).

Βήμα 2^ο - Υπολογισμός της τιμής της αντικειμενικής συνάρτησης z

Σύμφωνα με γνωστό θεώρημα η βέλτιστη ή βέλτιστες λύσεις ενός προβλήματος γραμμικού προγραμματισμού (αν υπάρχει), βρίσκεται σε κάποιο (ή κάποια) από τα ακραία σημεία – κορυφές της κλειστής κυρτής περιοχής εφικτών λύσεων του προβλήματος. Υπολογίζουμε τις συντεταγμένες των σημείων που ορίζουν την εφικτή περιοχή.

Σημείο Ο:

Σημείο Α:

Σημείο Β:

Για το σημείο Β έχουμε ότι είναι το σημείο τομής των ευθειών και οπότε λύνοντας το σύστημα το ζεύγος λύσεων είναι .

Σημείο Γ:

Το σημείο Γ είναι η τομή των ευθειών και , οπότε λύνοντας το σύστημα το ζεύγος λύσεων είναι .

Σημείο Δ:

Όμοια για το σημείο Δ έχουμε ότι είναι το σημείο τομής των ευθειών και , οπότε λύνοντας το σύστημα το ζεύγος λύσεων είναι .

Σημείο Ε:

Για κάθε ακραίο σημείο – κορυφή της περιοχής εφικτών λύσεων ΟΑΒΓΔΕ, υπολογίζουμε την τιμή της z. Έχουμε:

Σημείο και

Σημείο και

Σημείο και

Σημείο και

Σημείο και

Σημείο και

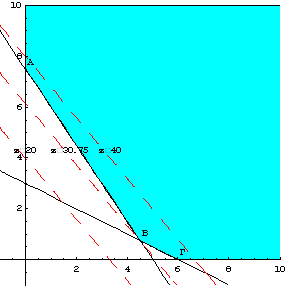
Δεδομένου ότι θέλουμε να μεγιστοποιήσουμε την αντικειμενική συνάρτηση , από τα παραπάνω προκύπτει ότι το σημείο είναι η βέλτιστη λύση του προβλήματος με τιμή της αντικειμενικής συνάρτησης .

Εναλλακτικά μπορούμε να λύσουμε το πρόβλημα με τον δεύτερο τρόπο, ο οποίος διαφοροποιείται στο βήμα εύρεσης της άριστης λύσης. Σχεδιάζουμε στην εφικτή περιοχή την ευθεία της αντικειμενικής συνάρτησης (ευθείες σταθερού κέρδους για μεγιστοποίηση κόστους για ελαχιστοποίηση) και προσπαθούμε να βρούμε το σημείο όπου η ισοκερδής εφάπτεται της εφικτής περιοχής πριν την εγκαταλείψει.

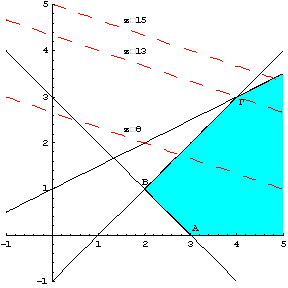
Αρχικά σχεδιάζουμε στην εφικτή περιοχή την ευθεία σταθερού κέρδους , δηλαδή, θεωρούμε ότι (σχήμα 2.10).

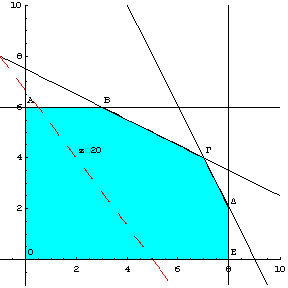
Σχήμα 2.10

Παρατηρούμε ότι η ευθεία σταθερού κέρδους διαπερνά την εφικτή περιοχή, άρα πρέπει να αυξήσουμε το κέρδος, δηλαδή, η ευθεία να μετατοπιστεί παράλληλα προς τα πάνω. Σχεδιάζουμε την ευθεία σταθερού κέρδους (σχήμα 2.11).

Σχήμα 2.11

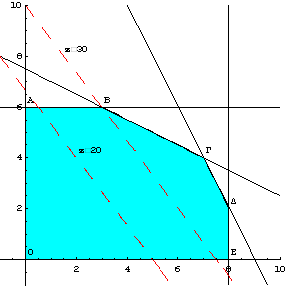
Παρατηρούμε ότι η ευθεία σταθερού κέρδους διαπερνά και αυτή την εφικτή περιοχή, άρα πρέπει να αυξήσουμε εκ νέου το κέρδος, δηλαδή, η ευθεία να μετατοπιστεί παράλληλα προς τα πάνω. Σχεδιάζουμε την ευθεία σταθερού κέρδους (σχήμα 2.12).

Σχήμα 2.12

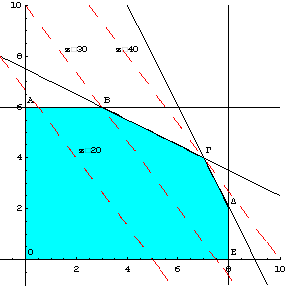
Παρατηρούμε ότι η ευθεία σταθερού κέρδους εφάπτεται στο σημείο Γ. Άρα η βέλτιστη λύση είναι το σημείο Γ με τιμή της αντικειμενικής συνάρτησης όσο και ο σταθερός όρος της αντίστοιχης ευθείας σταθερού κέρδους, δηλαδή, .

Οι συντεταγμένες του σημείου Γ είναι , επειδή, το σημείο Γ είναι η τομή των ευθειών και , οπότε λύνοντας το σύστημα το ζεύγος λύσεων είναι .

Η διαφορά των δυο μεθόδων είναι στον υπολογισμό της άριστης (βέλτιστης) λύσης. Στην πρώτη μέθοδο υπολογίζουμε οι συντεταγμένες όλων των σημείων της εφικτής περιοχής και η τιμή της αντικειμενικής συνάρτησης σε κάθε σημείο και επιλέγουμε την άριστη (βέλτιστη), ενώ, στην δεύτερη μέθοδο σχεδιάζουμε τις ευθείες σταθερού κέρδους (ή κόστους) και με παράλληλη μετατόπιση βρίσκουμε το σημείο που εφάπτεται η ευθεία πριν εγκαταλείψει την εφικτή περιοχή, η τιμή της αντικειμενικής συνάρτησης είναι ο σταθερός όρος της ευθείας και πρέπει να υπολογίσουμε τις συντεταγμένες του σημείου.

Το μειονέκτημα της δεύτερης μεθόδου είναι ότι πρέπει να ‘μαντέψουμε’ τον σταθερό όρο και μπορεί να χρειαστούμε πολλές δοκιμές, ενώ, το πλεονέκτημα της είναι ότι δεν υπολογίζουμε τις συντεταγμένες όλων των σημείων.

Τα επόμενα παραδείγματα και οι ασκήσεις έχουν λυθεί με την πρώτη μέθοδο.

Παράδειγμα 2.2

Πρόβλημα ελαχιστοποίησης

Να λυθεί το παρακάτω πρόβλημα γραμμικό προγραμματισμού:

με περιορισμούς

και

Ξεκινάμε με την συνθήκη μη αρνητικότητας των μεταβλητών η οποία μας περιορίζει γραφικά τις λύσεις στο πρώτο τεταρτημόριο, όπως φαίνεται στο σχήμα 2.13

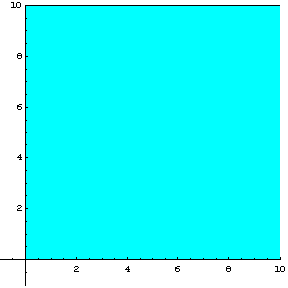
Σχήμα 2.13

Σχεδιάζουμε την ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.14

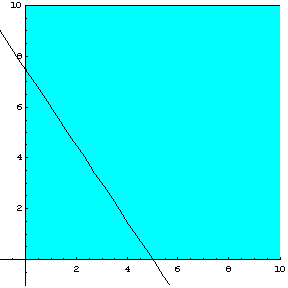
Σχήμα 2.14

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η νέα εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.15

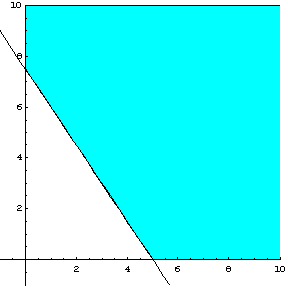
Σχήμα 2.15

Σχεδιάζουμε την δεύτερη ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.16

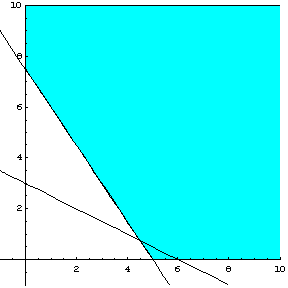
Σχήμα 2.16

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.17

Σχήμα 2.17

Η ανοικτή πολυγωνική περιοχή που σχηματίζεται είναι μη φραγμένη. Τα σημεία έχουν συντεταγμένες, , και .

Η τιμή που έχει η αντικειμενική συνάρτηση σε κάθε σημείο είναι:

.

Δεδομένου ότι θέλουμε να ελαχιστοποιήσουμε την αντικειμενική συνάρτηση , από τα παραπάνω προκύπτει ότι το σημείο είναι η βέλτιστη λύση του προβλήματος με τιμή της αντικειμενικής συνάρτησης .

Το γεγονός ότι η εφικτή περιοχή είναι μη φραγμένη δεν επηρεάζει την άριστη λύση γιατί το πρόβλημα είναι ελαχιστοποίησης και θέλουμε την μικρότερη δυνατή λύση.

Στο ίδιο συμπέρασμα καταλήγουμε εάν στην εφικτή περιοχή σχεδιάσουμε την ευθεία της αντικειμενικής συνάρτησης (ευθείες σταθερού κόστους , και ), η οποία ελαχιστοποιείται καθώς μετατοπίζεται παράλληλα προς τα κάτω, όπως φαίνεται στο σχήμα 2.18, και παρατηρούμε ότι εφάπτεται στο σημείο Β. Άρα η βέλτιστη λύση είναι το σημείο με τιμή της αντικειμενικής συνάρτησης όσο και ο σταθερός όρος της αντίστοιχης ευθείας σταθερού κέρδους, δηλαδή, .

Σχήμα 2.18

2.3 ΕΙΔΙΚΕΣ ΠΕΡΙΠΤΩΣΕΙΣ ΠΡΟΒΛΗΜΑΤΩΝ

Παράδειγμα 2.3

Πρόβλημα με άπειρες λύσεις.

Να λυθεί το παρακάτω πρόβλημα γραμμικό προγραμματισμού:

με περιορισμούς

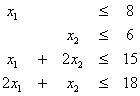
και

Παρατηρούμε ότι το παραπάνω πρόβλημα γραμμικού προγραμματισμού είναι το ίδιο με το παράδειγμα 2.1 με την διαφορά ότι η αντικειμενική συνάρτηση του προβλήματος είναι διαφορετική.

Εφόσον οι περιορισμοί με το παράδειγμα 2.1 είναι ίδιοι, τότε ίδια θα είναι και η εφικτή περιοχή του προβλήματος, η οποία φαίνεται στο σχήμα 2.19.

Σχήμα 2.19

Τα σημεία που ορίζουν την εφικτή περιοχή έχουν συντεταγμένες.

Σημείο Ο:

Σημείο Α:

Σημείο Β:

Σημείο Γ:

Σημείο Δ:

Σημείο Ε:

Για κάθε ακραίο σημείο – κορυφή της περιοχής εφικτών λύσεων ΟΑΒΓΔΕ, υπολογίζουμε την τιμή της . Έχουμε:

Σημείο και

Σημείο και

Σημείο και

Σημείο και

Σημείο και

Σημείο και

Δεδομένου ότι θέλουμε να μεγιστοποιήσουμε την αντικειμενική συνάρτηση , από τα παραπάνω προκύπτει ότι το σημείο , αλλά και το σημείο είναι οι βέλτιστες λύσεις του προβλήματος με τιμή της αντικειμενικής συνάρτησης .

Σε αυτή την περίπτωση οι βέλτιστες λύσεις είναι άπειρες και βρίσκονται όλες πάνω στο ευθύγραμμο τμήμα ΒΓ.

Στο ίδιο συμπέρασμα καταλήγουμε εάν στην εφικτή περιοχή σχεδιάσουμε την ευθεία της αντικειμενικής συνάρτησης (ευθείες σταθερού κέρδους , και ), η οποία μεγιστοποιείται καθώς μετατοπίζεται παράλληλα προς τα πάνω, όπως φαίνεται στο σχήμα 2.20, και παρατηρούμε ότι εφάπτεται, όχι σε ένα σημείο, αλλά σε ένα ευθύγραμμο τμήμα το ΒΓ. Σε αυτή την περίπτωση οι βέλτιστες λύσεις είναι άπειρες και βρίσκονται όλες πάνω στο ευθύγραμμο τμήμα ΒΓ με τιμή της αντικειμενικής συνάρτησης όσο και ο σταθερός όρος της αντίστοιχης ευθείας σταθερού κέρδους, δηλαδή, .

Σχήμα 2.20

Παράδειγμα 2.4

Πρόβλημα με μη φραγμένη εφικτή περιοχή με την τιμή της αντικειμενικής συνάρτησης να απειρίζεται.

Να λυθεί το παρακάτω πρόβλημα γραμμικό προγραμματισμού:

με περιορισμούς

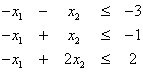
και

Ξεκινάμε με την συνθήκη μη αρνητικότητας των μεταβλητών η οποία μας περιορίζει γραφικά τις λύσεις στο πρώτο τεταρτημόριο, όπως φαίνεται στο σχήμα 2.21

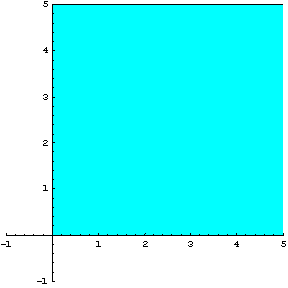
Σχήμα 2.21

Σχεδιάζουμε την ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.22

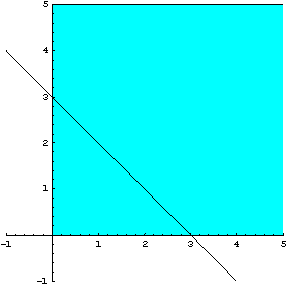
Σχήμα 2.22

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η νέα εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.23

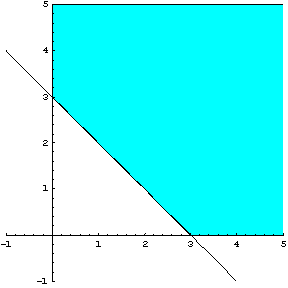
Σχήμα 2.23

Σχεδιάζουμε την δεύτερη ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.24

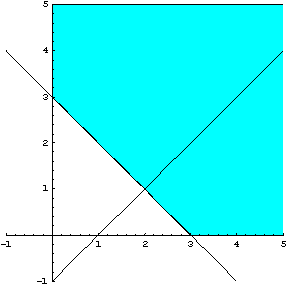
Σχήμα 2.24

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η νέα εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.25

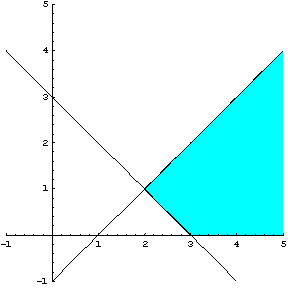
Σχήμα 2.25

Σχεδιάζουμε την τρίτη ευθεία η οποία έχει σημεία τομής με τους άξονες τα και .Η ευθεία φαίνεται στο σχήμα 2.26

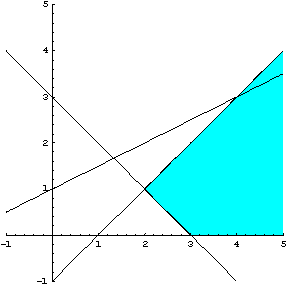
Σχήμα 2.26

Το σημείο επαληθεύει τον περιορισμό , άρα η εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.27.

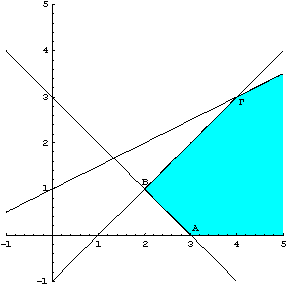
Σχήμα 2.27

Η ανοικτή πολυγωνική περιοχή που σχηματίζεται είναι μη φραγμένη. Τα σημεία έχουν συντεταγμένες , και .

Η τιμή που έχει η αντικειμενική συνάρτηση σε κάθε σημείο είναι:

.

Άριστη λύση έχουμε στο σημείο Γ, αλλά το σημείο Γ είναι σημείο της ευθείας που περιορίζει, αλλά, δεν φράζει την εφικτή περιοχή. Επομένως οποιοδήποτε (μεγαλύτερο) σημείο αυτής της ευθείας θα δίνει καλύτερη άριστη λύση. Για παράδειγμα το σημείο δίνει τιμή , το σημείο δίνει τιμή . Όσο κινούμαστε πάνω στην ευθεία και προς τα δεξιά, η τιμή της αντικειμενικής συνάρτησης αυξάνεται και βέβαια, επειδή η ευθεία εκτείνεται απεριόριστα η τιμή της αντικειμενικής συνάρτησης απειρίζεται.

Στο ίδιο συμπέρασμα καταλήγουμε εάν στην εφικτή περιοχή σχεδιάσουμε την ευθεία της αντικειμενικής συνάρτησης (ευθείες σταθερού κέρδους , και ), η οποία μεγιστοποιείται καθώς μετατοπίζεται παράλληλα προς τα πάνω, όπως φαίνεται στο σχήμα 2.28, και παρατηρούμε ότι μπορεί να μετατοπιστεί απεριόριστα αυξάνοντας κάθε φορά τον σταθερό όρο της ευθείας σταθερού κέρδους, πράγμα το οποίο μας υποδεικνύει ότι το πρόβλημα έχει μη φραγμένη εφικτή περιοχή με την τιμή της αντικειμενικής συνάρτησης να απειρίζεται.

Σχήμα 2.28

Παράδειγμα 2.5

Πρόβλημα χωρίς λύση

Να λυθεί το παρακάτω πρόβλημα γραμμικό προγραμματισμού:

με περιορισμούς

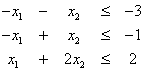
και

Ξεκινάμε με την συνθήκη μη αρνητικότητας των μεταβλητών η οποία μας περιορίζει γραφικά τις λύσεις στο πρώτο τεταρτημόριο, όπως φαίνεται στο σχήμα 2.29

Σχήμα 2.29

Σχεδιάζουμε την ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.30

Σχήμα 2.30

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η νέα εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.31

Σχήμα 2.31

Σχεδιάζουμε την δεύτερη ευθεία η οποία έχει σημεία τομής με τους άξονες τα και . Η ευθεία φαίνεται στο σχήμα 2.32

Σχήμα 2.32

Το σημείο δεν επαληθεύει τον περιορισμό , άρα η νέα εφικτή περιοχή είναι αυτή που φαίνεται στο σχήμα 2.33

Σχήμα 2.33

Σχεδιάζουμε την τρίτη ευθεία η οποία έχει σημεία τομής με τους άξονες τα και .Η ευθεία φαίνεται στο σχήμα 2.34

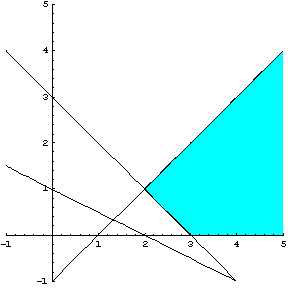
Σχήμα 2.34

Το σημείο επαληθεύει τον περιορισμό , άρα παρατηρούμε στο σχήμα 2.35

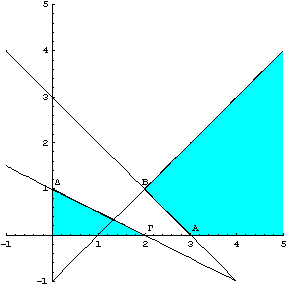
Σχήμα 2.35

ότι η εφικτή περιοχή είναι το κενό σύνολο, επειδή δεν υπάρχουν κοινά σημεία μεταξύ των δυο περιοχών.

Επομένως αφού η εφικτή περιοχή είναι κενό σύνολο δεν υπάρχουν βασικές εφικτές λύσεις και βεβαία ούτε άριστη λύση., δηλαδή, το πρόβλημα δεν έχει λύση.

2.4 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ

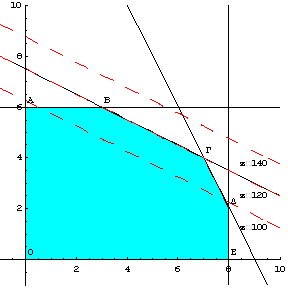
Η ανάλυση ευαισθησίας είναι μία μέθοδος η οποία εφαρμόζεται για να προσδιορίσει την ευαισθησία της λύσης ενός προβλήματος γραμμικού προγραμματισμού στις μεταβολές των παραμέτρων του. Συγκεκριμένα η γραφική λύση μας δίνει πληροφορίες που αφορούν

1) την άριστη λύση του προβλήματος γραμμικού προγραμματισμού

2) το διαχωρισμό των περιορισμών σε δεσμευτικούς ή χαλαρούς

3) τις δυϊκές τιμές

4) το εύρος αριστότητας των αντικειμενικών συντελεστών, δηλαδή, την αλλαγή που μπορούμε να κάνουμε σε ένα αντικειμενικό συντελεστή χωρίς να αλλάξει η άριστη λύση

5) το εύρος εφικτότητας των δεξιών μελών των περιορισμών, δηλαδή, την αλλαγή που μπορούμε να κάνουμε σε ένα δεξιό μέλος περιορισμού χωρίς να αλλάξει η εφικτή περιοχή ή χωρίς να αλλάξει η δυϊκή τιμή του περιορισμού.

Παράδειγμα 2.6

Να βρεθούν ποιοι περιορισμοί είναι χαλαροί και ποιοι δεσμευτικοί, οι δυϊκές τιμές, το εύρος αριστότητας για κάθε αντικειμενικό συντελεστή και το εύρος εφικτότητας για κάθε δεξιό μέλος περιορισμού (σταθερού όρου) στο παρακάτω πρόβλημα γραμμικό προγραμματισμού:

με περιορισμούς

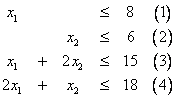
και

Όπως είδαμε στο παράδειγμα 2.1 το παραπάνω πρόβλημα γραμμικού προγραμματισμού έχει την εξής γραφική λύση (σχήμα 2.36)

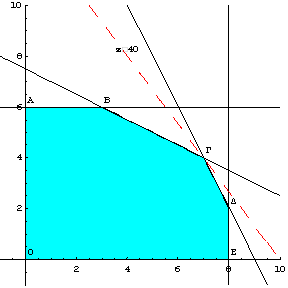
Σχημα 2.36

Η άριστη (βέλτιστη) λύση είναι , δηλαδή το σημείο Γ, με τιμή της αντικειμενικής συνάρτησης .

Οι περιορισμοί (3) και (4) οι οποίοι αντιστοιχούν στις ευθείες ΒΓ και ΓΔ είναι δεσμευτικοί γιατί συμμετέχουν στην λύση, ενώ οι περιορισμοί (1) και (2) οι οποίοι αντιστοιχούν στις ευθείες ΔΕ και ΑΒ είναι χαλαροί.

Οι δυϊκές τιμές των δεσμευτικών περιορισμών μπορούν να υπολογιστούν από των τύπο .

Ο τρίτος περιορισμός που αντιστοιχεί στην ευθεία ΒΓ είναι δεσμευτικός και μπορεί να αυξηθεί μέχρι να φτάσει το σημείο , ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο , άρα η δυϊκή τιμή του θα είναι .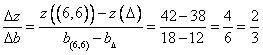

Ο τέταρτος περιορισμός που αντιστοιχεί στην ευθεία ΓΔ είναι δεσμευτικός και μπορεί να αυξηθεί μέχρι να φτάσει το σημείο , ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο , άρα η δυϊκή τιμή του θα είναι .

Για να βρούμε το εύρος αριστότητας ενός αντικειμενικού συντελεστή περιστρέφουμε την αντικειμενική ευθεία μέχρι να ταυτιστεί με κάποια άλλη ευθεία. Περιστρέφουμε την αντικειμενική ευθεία με κατεύθυνση την φορά κίνησης των δεικτών του ρολογιού και ταυτίζεται με την ευθεία ΓΔ, ενώ στην αντίθετη φορά περιστροφής ταυτίζεται με την ευθεία ΒΓ. Επομένως ο συντελεστής διεύθυνσης της αντικειμενικής ευθείας θα παίρνει τιμές μεταξύ των συντελεστών διεύθυνσης των ευθειών ΒΓ και ΓΔ. Θα ισχύει με και , άρα

Για σταθερό έχουμε, άρα

Για σταθερό έχουμε, άρα

Για να βρούμε το εύρος εφικτότητας ενός δεξιού μέλους δεσμευτικού περιορισμού μετατοπίζουμε την ευθεία που αντιστοιχεί στον περιορισμό και προς τις δυο κατευθύνσεις τόσο ώστε να μην αλλάζει η εφικτή περιοχή ή να μην αλλάζει η δυϊκή τιμή του περιορισμού ή το σημείο που αποτελεί την λύση να μην αλλάζει ευθεία. Για να βρούμε το εύρος εφικτότητας ενός δεξιού μέλους χαλαρού περιορισμού μετατοπίζουμε την ευθεία που αντιστοιχεί στον περιορισμό το σημείο που αποτελεί την λύση προς την μια κατεύθυνση και απεριόριστα προς την αντιθετη.

Ο πρώτος περιορισμός που αντιστοιχεί στην ευθεία ΔΕ είναι χαλαρός, άρα το μπορεί να αυξηθεί απεριόριστα, ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο Γ, δηλαδή, .

Ο δεύτερος περιορισμός που αντιστοιχεί στην ευθεία ΑΒ είναι χαλαρός, άρα το μπορεί να αυξηθεί απεριόριστα, ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο Γ, δηλαδή, .

Ο τρίτος περιορισμός που αντιστοιχεί στην ευθεία ΒΓ είναι δεσμευτικός, άρα το μπορεί να αυξηθεί μέχρι να φτάσει το σημείο , ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο , δηλαδή, .

Ο τέταρτος περιορισμός που αντιστοιχεί στην ευθεία ΓΔ είναι δεσμευτικός, άρα το μπορεί να αυξηθεί μέχρι να φτάσει το σημείο , ενώ μπορεί να μειωθεί μέχρι να φτάσει το σημείο , δηλαδή, .

ΚΕΦΑΛΑΙΟ 3

ΤΥΠΙΚΗ ΜΟΡΦΗ – ΒΑΣΙΚΕΣ ΛΥΣΕΙΣ

3.1 ΤΥΠΙΚΗ ΜΟΡΦΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ

Αν και η γεωμετρική ερμηνεία των προβλημάτων είναι αρκετά σημαντική δεν μπορεί να χρησιμοποιηθεί για όλα τα προβλήματα γραμμικού προγραμματισμού και αυτό γιατί στην πράξη τα περισσότερα προβλήματα γραμμικού προγραμματισμού έχουν περισσότερες από δύο μεταβλητές. Η κύρια μέθοδος επίλυσης προβλημάτων γραμμικού προγραμματισμού είναι η μέθοδος Simplex, ένας αλγόριθμος αριστοποίησης ο οποίος χαρακτηρίζεται από ένα αριθμό επαναλαμβανόμενων βημάτων τα οποία μπορούν να κωδικοποιηθούν στον Η/Υ. Πριν παρουσιάσουμε την μέθοδο αυτή (κεφάλαιο 4) θα διατυπώσουμε κάποιους βασικούς ορισμούς.

Το γενικό πρόβλημα γραμμικού προγραμματισμού μπορεί να διατυπωθεί ως εξής:

Να βρεθούν οι τιμές των μεταβλητών που μεγιστοποιούν ή ελαχιστοποιούν την συνάρτηση

Οι μεταβλητές πρέπει να ικανοποιούν τους περιορισμούς

και

όπου τα , , είναι γνωστές σταθερές.

Ορισμός 3.1

Ένα πρόβλημα γραμμικού προγραμματισμού είναι σε τυπική μορφή αν

1) είναι πρόβλημα μεγιστοποίησης

2) όλοι οι περιορισμοί είναι εξισώσεις με μη αρνητικούς τους σταθερούς ορούς (δεξιά μέλη περιορισμών)

3) όλες οι μεταβλητές είναι μη αρνητικές

Άρα η τυπική μορφή του προβλήματος γραμμικού προγραμματισμού είναι η εξής:

κάτω από τους περιορισμούς

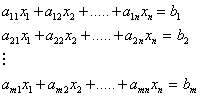
και , .

Ισοδύναμα με μορφή πινάκων το πρόβλημα γράφεται ως εξής:

όπου:

, , ,

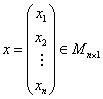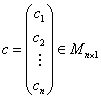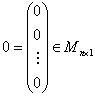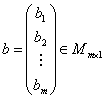
και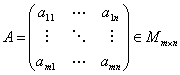

Με παριστάνουμε το διανυσματικό χώρο των πινάκων.

Υποθέτουμε ότι και ότι οι γραμμές του πίνακα Α είναι ανεξάρτητες.

3.2 ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΕ ΤΥΠΙΚΗ ΜΟΡΦΗ

Κάθε πρόβλημα γραμμικού προγραμματισμού μπορεί να αναχθεί στην τυπική μορφή με την χρήση στοιχειωδών μετασχηματισμών όπως οι παρακάτω:

Περιθώριες μεταβλητές

Περιορισμοί που εκφράζονται με ανισώσεις μπορούν να μετατραπούν σε εξισώσεις με την εισαγωγή νέων μη αρνητικών μεταβλητών οι οποίες μπορούν να μετατρέψουν τις ανισώσεις σε εξισώσεις. Οι μεταβλητές αυτές ονομάζονται περιθώριες. Υπάρχουν δύο είδη περιθώριων μεταβλητών οι χαλαρές και οι πλεονασματικές.

Χαλαρή μεταβλητή

Σε ένα περιορισμό της μορφής θεωρούμε μια νέα μεταβλητή , η οποία προστίθεται στο πρώτο μέλος της ανισότητας ώστε να έχουμε την ισότητα:

με .

Πιο απλά, προσθέτουμε μια νέα μη αρνητική μεταβλητή στο πρώτο μέλος έτσι ώστε τα δυο μέλη να γίνουν ίσα.

Θα ονομάζουμε την μια περιθώρια χαλαρή μεταβλητή.

Για παράδειγμα ένας περιορισμός της μορφής θα γραφεί στην μορφή όπου η είναι μια χαλαρή μεταβλητή.

Πλεονασματική μεταβλητή

Σε ένα περιορισμό της μορφής θεωρούμε μια νέα μεταβλητή , η οποία αφαιρείται από το πρώτο μέλος της ανισότητας ώστε να έχουμε την ισότητα:

Πιο απλά, αφαιρούμε μια νέα μη αρνητική μεταβλητή στο πρώτο μέλος έτσι ώστε τα δυο μέλη να γίνουν ίσα.

Θα ονομάζουμε την μια περιθώρια πλεονασματική μεταβλητή.

Για παράδειγμα, ο περιορισμός της μορφής θα γραφεί στην μορφή όπου η είναι μια πλεονασματική μεταβλητή.

Μετασχηματισμός προβλήματος ελαχιστοποίησης

Όταν ζητάμε να προσδιορίσουμε το ελάχιστο της αντικειμενικής συνάρτησης τότε θέτουμε και μεγιστοποιούμε την συνάρτηση .

Άρα , δηλαδή,

Για παράδειγμα η θα γίνει .

Μεταβλητές χωρίς περιορισμό στο πρόσημο

Αυτές οι μεταβλητές δεν υπόκεινται στον περιορισμό . Στην περίπτωση αυτή θέτουμε όπου .

Αν η μεταβλητή είναι μη θετική, θέτουμε , όπου .

Για παράδειγμα εάν έχω τον περιορισμό με και αγνώστου πρόσημου, τότε θέτω και ο περιορισμός γίνεται

Αρνητικοί σταθεροί όροι σε περιορισμούς

Εάν σε κάποιο περιορισμό ο σταθερός όρος είναι αρνητικός τότε πολλαπλασιάζοντας με (-1) γίνεται θετικός.

Δηλαδή ο περιορισμός θα γίνει

Παράδειγμα 3.1

Δίνεται το πρόβλημα γραμμικού προγραμματισμού

κάτω από τους περιορισμούς

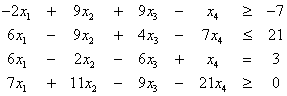
και ,

Να γραφεί στην τυπική του μορφή.

Το πρόβλημα είναι μεγιστοποίησης, επομένως δεν χρειάζεται μετατροπή στην αντικειμενική συνάρτηση.

Τον πρώτο περιορισμό θα τον πολλαπλασιάσουμε με για να γίνει θετικός ο σταθερός όρος και θα προσθέσουμε στο πρώτο μέλος μια περιθώρια μεταβλητή για να γίνει ισότητα.

Στον δεύτερο περιορισμό θα προσθέσουμε στο πρώτο μέλος μια περιθώρια μεταβλητή για να γίνει ισότητα.

Στον τρίτο περιορισμό δεν χρειάζεται να γίνει κάποια αλλαγή.

Στον τέταρτο περιορισμό θα αφαιρέσουμε στο πρώτο μέλος μια περιθώρια μεταβλητή για να γίνει ισότητα.

Θα αντικαταστήσουμε τις μεταβλητές αφού με τις και .

Άρα το πρόβλημα θα γίνει:

κάτω από τους περιορισμούς

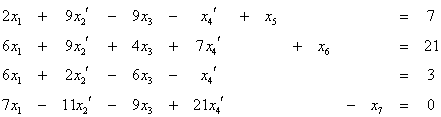
και

Παράδειγμα 3.2

Δίνεται το πρόβλημα γραμμικού προγραμματισμού

κάτω από τους περιορισμούς

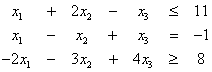
και ,

Να γραφεί στην τυπική του μορφή.

Το πρόβλημα είναι ελαχιστοποίησης, επομένως πρέπει να το μετατρέψουμε σε πρόβλημα μεγιστοποίησης.

Στον πρώτο περιορισμό θα προσθέσουμε στο πρώτο μέλος μια περιθώρια μεταβλητή για να γίνει ισότητα.

Τον δεύτερο περιορισμό θα τον πολλαπλασιάσουμε με για να γίνει θετικός ο σταθερός όρος.

Στον τρίτο περιορισμό θα αφαιρέσουμε στο πρώτο μέλος μια περιθώρια μεταβλητή για να γίνει ισότητα.

Θα αντικαταστήσουμε την μεταβλητή αφού με την και .

Θα αντικαταστήσουμε την μεταβλητή , η οποία δεν υπόκειται σε κάποιο περιορισμό, με τις και έτσι ώστε .

Άρα το πρόβλημα θα γίνει:

κάτω από τους περιορισμούς

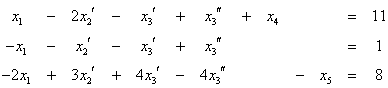
και

3.3 ΒΑΣΙΚΕΣ ΛΥΣΕΙΣ

Όπως είδαμε το πρόβλημα μπορεί να γραφεί με την βοήθεια πινάκων ως εξής:

όπου:

, , ,

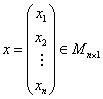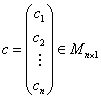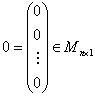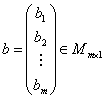
και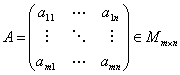

Με παριστάνουμε το διανυσματικό χώρο των πινάκων.

Στην τυπική μορφή του προβλήματος το σύστημα έχει μεταβλητές και γραμμικές εξισώσεις με .

Βασική λύση είναι μία λύση που προκύπτει αν θέσουμε μεταβλητές ίσες με το μηδέν και λύσουμε ως προς τις υπόλοιπες μεταβλητές υπό τον όρο το γραμμικό σύστημα που προκύπτει να περιλαμβάνει από τις στήλες (διανύσματα) του πίνακα Α έτσι ώστε τα διανύσματα αυτά να είναι γραμμικώς ανεξάρτητα.

Δηλαδή ο πίνακας Α να περιέχει έναν υποπίνακα διάστασης για τον οποίο ισχύει ότι η ορίζουσα του είναι διάφορη του μηδενός. Η τετραγωνικός πίνακας, που προκύπτει από τον Α και έχει γραμμικά ανεξάρτητες στήλες καλείται βάση του συστήματος ενώ οι μεταβλητές που αντιστοιχούν στις στήλες της βάσεως καλούνται βασικές μεταβλητές. Οι υπόλοιπες μεταβλητές που δεν περιλαμβάνονται στη βάση καλούνται μη βασικές μεταβλητές. Αν συμβολίσουμε τον υποπίνακα των γραμμικά ανεξάρτητων στηλών του Α με Β, επειδή , η βασική λύση μπορεί να υπολογιστεί από την σχέση , όπου είναι το διάνυσμα των βασικών μεταβλητών. Ο πίνακας Β ονομάζεται και βασικός πίνακας.

Θεώρημα 3.1

Ο αριθμός των βασικών λύσεων ενός προβλήματος γραμμικού προγραμματισμού είναι πεπερασμένος και το πολύ .

Βασική εφικτή λύση είναι μία βασική λύση όπου όλες οι βασικές μεταβλητές είναι μη αρνητικές.

Μη εκφυλισμένη βασική εφικτή λύση είναι μία βασική εφικτή λύση με ακριβώς θετικά . Επομένως, μία εκφυλισμένη βασική εφικτή λύση έχει λιγότερα από θετικά , δηλαδή, εκφυλισμένη βασική εφικτή λύση είναι αυτή που έχει μια τουλάχιστον από τις βασικές λύσεις ίση με μηδέν.

Θεώρημα 3.2

Αν ένα πρόβλημα γραμμικού προγραμματισμού έχει ένα μη κενό σύνολο εφικτών λύσεων, τότε το σύνολο αυτό περιέχει τουλάχιστον μια βασική λύση.

Θεώρημα 3.3

Η εφικτή περιοχή ενός προβλήματος γραμμικού προγραμματισμού είναι κυρτό σύνολο.

Θεώρημα 3.4

Αν μια βασική εφικτή λύση, τότε κορυφή της και αντίστροφα αν είναι κορυφή της , τότε η είναι μια βασική εφικτή λύση.

Ορισμός 3.2

Άριστη λύση ενός προβλήματος γραμμικού προγραμματισμού είναι κάθε εφικτή λύση που μεγιστοποιεί την αντικειμενική συνάρτηση.

Θεώρημα 3.5

Έστω το πρόβλημα γραμμικού προγραμματισμού , με εφικτή περιοχή το σύνολο . Αν το είναι φραγμένο σύνολο, τότε το πρόβλημα γραμμικού προγραμματισμού έχει άριστη λύση.

Θεώρημα 3.6

Αν η εφικτή περιοχή είναι ένα φραγμένο σύνολο, τότε η άριστη λύση πετυχαίνεται σε μια κορυφή της .

Θεώρημα 3.7

Αν σε ένα πρόβλημα γραμμικού προγραμματισμού έχουμε δυο ή περισσότερες άριστες λύσεις, τότε κάθε κυρτός συνδυασμός τους είναι άριστη λύση.

Ορισμός 3.3

Ένα σύνολο λέγεται κυρτό, αν δοθέντος δύο σημείων , το σημείο για κάθε .

Ως κυρτός συνδυασμός των σημείων ορίζεται κάθε σημείο της μορφής

με και

Ορισμός 3.4

Ακρότατο σημείο (κορυφή) ενός κυρτού συνόλου είναι κάθε σημείο για το οποίο δεν υπάρχουν τέτοια ώστε

Παράδειγμα 3.3

Να βρεθούν οι βασικές λύσεις του συστήματος

με .

Το σύστημα έχει μεταβλητές και εξισώσεις άρα θα έχουμε το πολύ 6 βασικές λύσεις, γιατί

Ο πίνακας Α είναι .

Μηδενίζουμε ανά δυο τις μεταβλητές και έχουμε:

1)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

2)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

3)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

4)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

5) Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

6) Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

Συνοψίζουμε τα αποτελέσματα σε ένα πίνακα

α/α	Λύση	Βασικές μεταβλητές	Παρατηρήσεις
1			βασική λύση
2			βασική λύση
3			βασική λύση
4			βασική εφικτή λύση
5			βασική εφικτή λύση
6			βασική εφικτή λύση

Παράδειγμα 3.4

Δίνεται το παρακάτω πρόβλημα γραμμικού προγραμματισμού

κάτω από τους περιορισμούς

με .

Να βρεθούν όλες οι βασικές λύσεις του προβλήματος και έπειτα να βρεθεί η άριστη λύση.

Αρχικά μετατρέπουμε το πρόβλημα γραμμικού προγραμματισμού στην τυπική του μορφή.

κάτω από τους περιορισμούς

με

Το σύστημα έχει μεταβλητές και εξισώσεις άρα θα έχουμε το πολύ 6 βασικές λύσεις, γιατί

Ο πίνακας Α είναι .

Μηδενίζουμε ανά δυο τις μεταβλητές και έχουμε:

1)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

2)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

3)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

4)Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

5) Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

6) Για , ο πίνακας Β είναι με , άρα το σύστημα θα γίνει

το οποίο έχει λύση .

Συνοψίζουμε τα αποτελέσματα σε ένα πίνακα

α/α	Λύση	Βασικές μεταβλητές	Παρατηρήσεις
1			βασική εφικτή λύση
2			βασική εφικτή λύση
3			βασική λύση
4			βασική λύση
5			βασική εφικτή λύση
6			βασική εφικτή λύση

Για βρούμε την άριστη λύση υπολογίζουμε την τιμή της αντικειμενικής συνάρτησης για κάθε βασική εφικτή λύση.

Για , έχουμε ,

για , έχουμε

για , έχουμε

για , έχουμε

Άρα η βέλτιστη λύση είναι με τιμή της αντικειμενικής συνάρτησης .

Το πρόβλημα αυτό μπορεί να λυθεί και γραφικά.

Η εφικτή περιοχή είναι η πολυγωνική περιοχή που περικλείεται από τα σημεία ΟΑΒΓ όπως φαίνεται στο σχήμα 3.1.

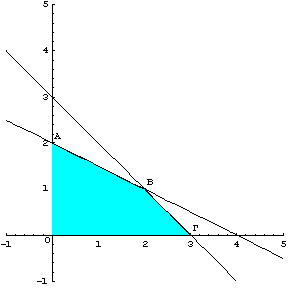
Σχήμα 3.1

Τα σημεία έχουν τις εξής συντεταγμένες: , , και .

Παρατηρούμε ότι τα σημεία ταυτίζονται με τις βασικές εφικτές λύσεις.

α/α	Λύση	Βασικές μεταβλητές	Παρατηρήσεις	Σημείο
1			βασική εφικτή λύση	Ο
2			βασική εφικτή λύση	Α
3			βασική λύση
4			βασική λύση
5			βασική εφικτή λύση	Γ
6			βασική εφικτή λύση	Β

Με την βοήθεια των βασικών λύσεων, έχουμε ακόμη ένα τρόπο λύσης για προβλήματα γραμμικού προγραμματισμού. Η μεθοδολογία αυτού του τρόπου υλοποιείται με τα παρακάτω βήματα:

1. Μετατροπή στην τυπική μορφή του προβλήματος γραμμικού προγραμματισμού.

2. Εύρεση όλων των βασικών λύσεων του προβλήματος.

3. Εντοπισμός μεταξύ αυτών, των βασικών εφικτών λύσεων.

4. Εύρεση της βασικής εφικτής λύσης (βασικών εφικτών λύσεων)

η οποία μεγιστοποιεί την αντικειμενική συνάρτηση.

Το μειονέκτημα αυτής της μεθόδου είναι ότι έχουμε πολλές περιπτώσεις, ακόμη και για μικρού μεγέθους προβλήματα.

π.χ. για μεταβλητές και περιορισμούς έχουμε το πολύ

βασικές λύσεις, οι οποίες είναι αδύνατον να βρεθούν με την παραπάνω μέθοδο λύσης.

ΚΕΦΑΛΑΙΟ 4

ΜΕΘΟΔΟΣ SIMPLEX

Η βέλτιστη λύση όπως παρατηρήθηκε προηγουμένως αντιστοιχεί σε μια κορυφή στη γεωμετρική απεικόνιση του εφικτού συνόλου. Η μέθοδος Simplex ξεκινώντας από μια αρχική κορυφή μπορεί να πάει σε άλλες γειτονικές κορυφές κατά μήκος των ακμών του πολυγώνου του εφικτού συνόλου. Σε κάθε μετάβαση της μεθόδου από μία κορυφή σε μια άλλη η μέθοδος Simplex κατορθώνει να βρει την ακμή που την οδηγεί σε μια κορυφή, η οποία δίνει βελτιωμένη τιμή στην αντικειμενική συνάρτηση. Συνεχίζοντας κατά αυτό τον τρόπο η τιμή της αντικειμενικής συνάρτησης από κορυφή σε κορυφή βελτιώνεται και τελικά φτάνουμε σε μια κορυφή όπου η αντικειμενική συνάρτηση βελτιστοποιείται. Οποιαδήποτε άλλη κορυφή δίνει χειρότερη λύση και έτσι η διαδικασία τερματίζεται.

Η μέθοδος Simplex είναι μια αλγεβρική επαναληπτική διαδικασία όπου σε κάθε βήμα έχουμε μια νέα βασική εφικτή λύση προβλημάτων της μορφής:

Στη συνέχεια πρέπει να εξετάσουμε αν η τρέχουσα βασική εφικτή λύση είναι και η βέλτιστη. Συνεπώς χρειαζόμαστε έναν έλεγχο για το αν η λύση είναι η βέλτιστη. Αν είναι τότε η διαδικασία τερματίζεται. Αν η τρέχουσα βασική λύση δεν είναι βέλτιστη τότε χρειαζόμαστε μια μέθοδο με την οποία θα μπορούμε να βρούμε μία καλύτερη βασική βέλτιστη λύση. Η διαδικασία θα περατωθεί ως ένα πεπερασμένο πλήθος βημάτων, επειδή ο αριθμός των βασικών εφικτών λύσεων είναι πεπερασμένος, και αν η λύση δεν επιστρέψει σε κάποια προηγούμενη τελικά θα φθάσουμε στην βέλτιστη. Σημαντικό στοιχείο της μεθόδου αποτελεί και το γεγονός ότι εντοπίζει και τις περιπτώσεις στις οποίες το πρόβλημα είναι αδύνατο ή έχει μη πεπερασμένη λύση.

4.1 ΑΛΓΟΡΙΘΜΟΣ ΜΕΘΟΔΟΥ SIMPLEX – SIMPLEX TABLEAU

Τα βασικά σημεία του αλγόριθμου Simplex είναι:

1. Υπολογίζουμε μια αρχική βασική λύση , επιλέγοντας τη βάση Β από τις στήλες του πίνακα Α, με κατάλληλη επιλογή μεταξύ των γραμμικώς ανεξάρτητων στηλών του πίνακα Α.

2. Εκφράζουμε τα διανύσματα (στήλες) του πίνακα Α που δεν ανήκουν στην βάση συναρτήσει των διανυσμάτων της βάσης και υπολογίζουμε τα αντίστοιχα σύμφωνα με την σχέση: , όπου η στήλη του πίνακα Α.

3. Υπολογίζουμε τις τιμές για τα διανύσματα εκτός βάσης εφαρμόζοντας τη σχέση .

4. Υπολογίζουμε τις ποσότητες . Αν για όλα τα ισχύει ότι , τότε έχουμε βέλτιστη λύση

5. Αν ένα ή περισσότερα , επιλέγουμε ένα διάνυσμα από τα εκτός βάσης για να εισέλθει στη βάση, εφαρμόζοντας το επόμενο κριτήριο:

.

6. Αν όλα τα , τότε υπάρχει μια μη φραγμένη λύση. Αν ένα τουλάχιστον , επιλέγουμε το διάνυσμα που θα φύγει από τη βάση σύμφωνα με το κριτήριο:

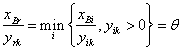
7. Υπολογίζουμε την νέα βάση B η οποία προκύπτει από την προηγούμενη αντικαθιστώντας το διάνυσμα με το νέο . Υπολογίζουμε την νέα βασική εφικτή λύση , με τις σχέσεις :

και τις νέες τιμές των , , .

8. Επιστρέφουμε στο δεύτερο βήμα και επαναλαμβάνουμε την διαδικασία.

Ο Αλγόριθμος Simplex είναι εκθετικού χρόνου.

Αν και υπάρχουν παραδείγματα που επιβεβαιώνουν το παραπάνω, στην πράξη κάτι τέτοιο δεν συμβαίνει γι’ αυτό και η μέθοδος Simplex χρησιμοποιείται ευρύτατα. Το 1979 ο Khachiyan ανακάλυψε τον πρώτο πολυωνυμικό αλγόριθμο για τον γραμμικό προγραμματισμό την ελλειψοειδή μέθοδο, η οποία δεν είχε όμως μεγάλο πρακτικό ενδιαφέρον γιατί στις περισσότερες πρακτικές εφαρμογές έδινε χειρότερα αποτελέσματα από την μέθοδο Simplex. Τελικά το 1984 ο Karmarkar ανακάλυψε έναν άλλον πολυωνυμικό αλγόριθμο που είχε και πρακτικά αποτελέσματα καλύτερα από την μέθοδο Simplex.

Το Simplex tableau

Η επίλυση των προβλημάτων γραμμικού προγραμματισμού με τα Simplex tableau αποτελεί ένα συστηματικό τρόπο καταχώρησης των απαραίτητων ποσοτήτων, έτσι ώστε τα αναγκαία βήματα εφαρμογής του αλγορίθμου Simplex να μπορούν να εκτελούνται με ποιο απλό , σύντομο και αποτελεσματικό τρόπο. Τα βήματα που ακολουθούμε είναι τα εξής:

Βήμα 1ο:

Διατύπωση προβλήματος γραμμικού προγραμματισμού.

Βήμα 2ο:

Τυπική μορφή προβλήματος γραμμικού προγραμματισμού.

ΕΑΝ μπορεί να σχηματιστεί μοναδιαίος πίνακας με κάποιες στήλες του πίνακα Α ΤΟΤΕ

πάμε στο βήμα 3

ΑΛΛΙΩΣ

πρέπει να προσθέσουμε στο πρόβλημα τεχνητές μεταβλητές έτσι ώστε να δημιουργηθεί ο μοναδιαίος πίνακας με κάποιες στήλες του πίνακα Α και να συνεχίσουμε στο βήμα 3

Βήμα 3ο:

Κατασκευή Simplex tableau

Βήμα 4ο:

ΕΑΝ , ΤΟΤΕ

ΤΕΛΟΣ (άριστη λύση)

ΑΛΛΙΩΣ

Βήμα 5ο:

ΕΑΝ και , ΤΟΤΕ

ΤΕΛΟΣ (μη πεπερασμένη λύση)

ΑΛΛΙΩΣ

Βήμα 6ο:

Βασική γίνεται η στήλη για την οποία .

Βήμα 7ο:

Φεύγει από τη βάση η στήλη για την οποία .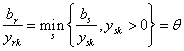

Βήμα 8ο:

Καθορισμός στοιχείου πιλότου .

Βήμα 9ο:

Χρησιμοποιώντας τους τύπους (απαλοιφής):

κατασκεύασε το επόμενο Simplex tableau και στη συνέχεια πήγαινε στο Βήμα 4.

Παράδειγμα 4.1

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

και

Αρχικά μετατρέπουμε το πρόβλημα γραμμικού προγραμματισμού στην τυπική μορφή, δηλαδή, να είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών να είναι θετικά, οι ανισώσεις να γίνουν ισότητες και όλες οι μεταβλητές να είναι θετικές.

Θα ορίσουμε 2 περιθώριες μεταβλητές για να μετατρέψουμε τις ανισώσεις σε ισότητες.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

και

Το αρχικό Simplex tableau είναι:

			3	8	0	0
B		β					θ
	0	24	1	3	1	0
	0	20	1	2	0	1
	z	0	-3	-8	0	0

Στην τελευταία γραμμή έχουμε τις ποσότητες , οι οποίες έχουν τιμές , , και .

Η τρέχουσα βασική λύση δεν είναι η άριστη (βέλτιστη) επειδή υπάρχει αρνητική ποσότητα .

Συνεχίζουμε με την επιλογή εισερχόμενης μεταβλητής σύμφωνα με τον τύπο , δηλαδή, επιλέγουμε από τα αρνητικά το μεγαλύτερο κατά απόλυτη τιμή.

Άρα η μεταβλητή (στήλη) που μπαίνει στη βάση είναι η και .

Έπειτα επιλέγουμε την εξερχόμενη μεταβλητή αφού πρώτα υπολογίσουμε τους λογούς 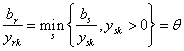, οι οποίοι είναι και . Επιλέγουμε από τους θετικούς λόγους τον μικρότερο.

Άρα η μεταβλητή που φεύγει από την βάση είναι η και .

Πιλότος είναι το .

Αξονική γραμμή είναι η 1^η και αξονική στήλη η 2^η όπως φαίνεται και από την γραμμοσκίαση στο παρακάτω Simplex tableau

			3	8	0	0
B		β					θ
	0	24	1	3	1	0	8
	0	20	1	2	0	1	10
	z	0	-3	-8	0	0

Επόμενο βήμα είναι ο υπολογισμός του νέου Simplex tableau χρησιμοποιώντας τους τύπους και , δηλαδή,

Άρα υπολογίζουμε πρώτα την αξονική γραμμή του νέου tableau και έχουμε

.

Έπειτα υπολογίζουμε όλες τις άλλες γραμμές του νέου tableau

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			3	8	0	0
B		β					θ
	8	8		1		0
	0	4		0		1
	z	64		0		0

Στην τελευταία γραμμή έχουμε τις ποσότητες , οι οποίες έχουν τιμές , , και .

Η τρέχουσα βασική λύση δεν είναι η άριστη (βέλτιστη) επειδή υπάρχει αρνητική ποσότητα .

Συνεχίζουμε με την επιλογή εισερχόμενης μεταβλητής σύμφωνα με τον τύπο , δηλαδή, επιλέγουμε από τα αρνητικά το μεγαλύτερο κατά απόλυτη τιμή.

Άρα η μεταβλητή (στήλη) που μπαίνει στη βάση είναι η και .

Έπειτα επιλέγουμε την εξερχόμενη μεταβλητή αφού πρώτα υπολογίσουμε τους λογούς 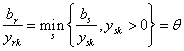, οι οποίοι είν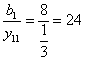αι και 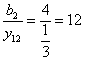. Επιλέγουμε από τους θετικούς λόγους τον μικρότερο.

Άρα η μεταβλητή που φεύγει από την βάση είναι η και .

Πιλότος είναι το .

Αξονική γραμμή είναι η 2^η και αξονική στήλη η 1^η όπως φαίνεται και από την γραμμοσκίαση στο παρακάτω Simplex tableau

			3	8	0	0
B		β					θ
	8	8		1		0	24
	0	4		0		1	12
	z	64		0		0

και υπολογίζουμε το νέο Simplex tableau με τους τύπους:

για την αξονική γραμμή του νέου Simplex tableau

για τις άλλες γραμμές

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			3	8	0	0
B		β					θ
	8	4	0	1	1	-1
	3	12	1	0	-2	3
	z	68	0	0	2	1

Στην τελευταία γραμμή έχουμε τις ποσότητες , οι οποίες έχουν τιμές , , και .

Η τρέχουσα βασική λύση είναι η άριστη (βέλτιστη) επειδή δεν υπάρχει αρνητική ποσότητα .

Άρα η άριστη (βέλτιστη) λύση είναι με τιμή της αντικειμενικής συνάρτησης .

4.2 ΠΡΟΒΛΗΜΑ ΜΕ ΑΠΕΙΡΕΣ ΛΥΣΕΙΣ

Όπως είδαμε στο προηγούμενο παράδειγμα (4.1) όταν για όλες τις ποσότητες ισχύει , η μέθοδος Simplex τερματίζει και έχουμε άριστη (βέλτιστη) λύση. Οι βασικές μεταβλητές έχουν τις αντίστοιχες ποσότητες ίσες με το μηδέν και οι μη βασικές μεταβλητές έχουν τις αντίστοιχες ποσότητες διάφορες από το μηδέν. Εντούτοις, αν κάποια μη βασική μεταβλητή αντιστοιχεί σε , τότε αύξηση της τιμής της δε αλλάζει την τιμή της αντικειμενικής συνάρτησης. Με την προϋπόθεση ότι η λύση είναι μη εκφυλισμένη, αν εισάγουμε την μεταβλητή αυτή στην βάση θα μας οδηγήσει σε μια εναλλακτική άριστη (βέλτιστη) λύση με την ίδια, βεβαίως, τιμή της αντικειμενικής συνάρτησης. Επομένως το πρόβλημα θα έχει άπειρες λύσεις.

Παράδειγμα 4.2

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

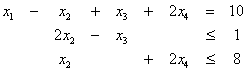
και

Αρχικά μετατρέπουμε το πρόβλημα γραμμικού προγραμματισμού στην τυπική μορφή, δηλαδή, να είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών να είναι θετικά, οι ανισώσεις να γίνουν ισότητες και όλες οι μεταβλητές να είναι θετικές.

Θα ορίσουμε 2 περιθώριες μεταβλητές για να μετατρέψουμε τις ανισώσεις σε ισότητες.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

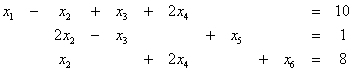
και .

Το αρχικό Simplex tableau είναι:

			-1	2	-3	0	0	0
B		β							θ
	-1	10	1	-1	1	2	0	0	5
	0	1	0	2	-1	0	1	0	--
	0	8	0	1	0	2	0	1	4
	z	-10	0	-1	2	-2	0	0

Έχουμε και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			-1	2	-3	0	0	0
B		β							θ
	-1	2	1	-2	1	0	0	-1
	0	1	0	2	-1	0	1	0
	0	4	0		0	1	0
	z	-2	0	0	2	0	0	1

και επειδή όλες οι ποσότητες είναι θετικές ή μηδέν αυτό είναι το τελικό Simplex tableau.

Επομένως η άριστη λύση του προβλήματος είναι με τιμή της αντικειμενικής συνάρτησης .

Παρατηρούμε ότι στο τελικό Simplex tableau έχουμε , παρόλο που η μεταβλητή (στήλη ) δεν είναι βασική. Δηλαδή, η εισαγωγή της μεταβλητής (στήλης ) στη βάση μας δίνει μια εναλλακτική άριστη λύση.

Πράγματι, εάν εισάγουμε την μεταβλητή στην θέση της θα έχουμε το εξής Simplex tableau

			-1	2	-3	0	0	0
B		β							θ
	-1	3	1	0	0	0	0	-1
	2		0	1		0		0
	0		0	0		1
	z	-2	0	0	2	0	0	1

το οποίο μας δίνει άριστη λύση και φυσικά με τιμή της αντικειμενικής συνάρτησης .

Άρα το πρόβλημα γραμμικού προγραμματισμού έχει άπειρες άριστες λύσεις της μορφής , όπου και .

Επομένως με .

4.3 ΠΡΟΒΛΗΜΑ ΜΗ ΦΡΑΓΜΕΝΟ

Σε ένα Simplex tableau έχουμε επιλέξει την μεταβλητή που θα εισαχθεί στην βάση έστω ότι είναι η και προσπαθούμε να εντοπίσουμε την εξερχόμενη μεταβλητή. Παρατηρούμε ότι για όλα τα ισχύει , δηλαδή, όλοι οι λόγοι θ είναι αρνητικοί το οποίο μας οδηγεί στο συμπέρασμα ότι η μεταβλητή μπορεί να αυξηθεί απεριόριστα. Επομένως η τιμή της αντικειμενικής συνάρτησης θα τείνει στο άπειρο, δηλαδή, το πρόβλημα είναι μη φραγμένο.

Παράδειγμα 4.3

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

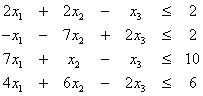
και

Αρχικά μετατρέπουμε το πρόβλημα γραμμικού προγραμματισμού στην τυπική μορφή, δηλαδή, να είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών να είναι θετικά, οι ανισώσεις να γίνουν ισότητες και όλες οι μεταβλητές να είναι θετικές.

Θα μετατρέψουμε το πρόβλημα ελαχιστοποίησης σε μεγιστοποίησης και θα ορίσουμε 4 περιθώριες μεταβλητές για να μετατρέψουμε τις ανισώσεις σε ισότητες.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

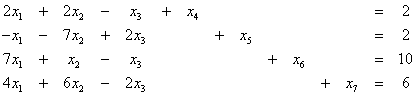
και

Το αρχικό Simplex tableau είναι:

			-1	-1	1	0	0	0	0
B		β								θ
	0	2	2	2	-1	1	0	0	0	--
	0	2	-1	-7	2	0	1	0	0	1
	0	10	7	1	-1	0	0	1	0	--
	0	6	4	6	-2	0	0	0	1	--
	z	0	1	1	-1	0	0	0	0

Έχουμε , άρα εισερχόμενη μεταβλητή είναι η . Επειδή εξερχόμενη μεταβλητή είναι η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			-1	-1	1	0	0	0	0
B		β								θ
	0	3			0	1		0	0
	1	1			1	0		0	0
	0	11			0	0		1	0
	0	8	3	-1	0	0	1	0	1
	Z	1			0	0		0	0

Έχουμε, , άρα, εισερχόμενη μεταβλητή είναι η , αλλά όλα τα είναι αρνητικά (η στήλη ) και έτσι όλοι οι λόγοι θ είναι αρνητικοί. Καταλήγουμε λοιπόν στο συμπέρασμα ότι το πρόβλημα γραμμικού προγραμματισμού είναι μη φραγμένο.

4.4 ΠΡΟΒΛΗΜΑ ΜΕ ΕΚΦΥΛΙΣΜΕΝΕΣ ΛΥΣΕΙΣ

Σε ένα Simplex tableau παρατηρούμε ότι η τρέχουσα βασική λύση (στήλη β) έχει σε μια μεταβλητή την τιμή μηδέν. Αυτό μας υποδεικνύει την ύπαρξη εκφυλισμένης λύσης την οποία την αντιμετωπίζουμε με την αντικατάσταση του μηδέν της βασικής μεταβλητής με ένα αυθαίρετα μικρό θετικό . Έπειτα συνεχίζουμε κανονικά μέχρι την εύρεση του τελικού Simplex tableau. Στην άριστη λύση θέτουμε .

Παράδειγμα 4.4

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

και

Αρχικά μετατρέπουμε το πρόβλημα γραμμικού προγραμματισμού στην τυπική μορφή, δηλαδή, να είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών να είναι θετικά, οι ανισώσεις να γίνουν ισότητες και όλες οι μεταβλητές να είναι θετικές.

Θα ορίσουμε 2 περιθώριες μεταβλητές για να μετατρέψουμε τις ανισώσεις σε ισότητες.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

και

Το αρχικό Simplex tableau είναι:

			4	2	1	0	0
B		β						θ
	0	1	1	1	0	1	0	1
	0	1	1	0	1	0	1	1
	z	0	-4	-2	-1	0	0

Έχουμε , και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			4	2	1	0	0
B		β						θ
	4	1	1	1	0	1	0
	0	0	0	-1	1	-1	1
	z	4	0	2	-1	4	0

Παρατηρούμε στο τρέχον Simplex tableau ότι η βασική μεταβλητή έχει λύση μηδέν, δηλαδή, είναι εκφυλισμένη. Αντικαθιστούμε την τιμή 0 της βασικής μεταβλητής με έναν αυθαίρετο πολύ μικρό θετικό αριθμό και θα έχουμε

			4	2	1	0	0
B		β						θ
	4	1	1	1	0	1	0	--
	0		0	-1	1	-1	1
	z	4	0	2	-1	4	0

Έχουμε, , άρα, εισερχόμενη μεταβλητή είναι η , ενώ εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			4	2	1	0	0
B		β						θ
	4	1	1	1	0	1	0
	1		0	-1	1	-1	1
	z		0	2	0	3	1

και επειδή όλες οι ποσότητες είναι θετικές ή μηδέν, αυτό είναι το τελικό Simplex tableau.

Επομένως η άριστη (βέλτιστη) λύση του προβλήματος είναι, αφού θέσουμε , με τιμή της αντικειμενικής συνάρτησης .

4.5 Μ – ΜΕΘΟΔΟΣ

Η υλοποίηση και εφαρμογή της μεθόδου Simplex, αλλά και των Simplex tableau, απαιτεί το πρόβλημα γραμμικού προγραμματισμού να είναι στην τυπική μορφή αλλά και την ύπαρξη του μοναδιαίου πίνακα μέσα από τις στήλες του πίνακα Α.

Στην περίπτωση που δεν περιέχεται ο μοναδιαίος πίνακας μέσα στον πίνακα Α χρησιμοποιούμε τεχνητές μεταβλητές έτσι ώστε να δημιουργηθεί ο μοναδιαίος πίνακας.

Η εισαγωγή τεχνητών μεταβλητών διευρύνει την εφικτή περιοχή του προβλήματος. Βλέπουμε ότι μια εφικτή λύση στο αναθεωρημένο πρόβλημα είναι εφικτή λύση και για το αρχικό πρόβλημα αν και μόνον αν οι τιμές όλων των τεχνητών μεταβλητών είναι μηδέν.

Η Μ-μέθοδος εισάγει τις τεχνητές μεταβλητές στην αντικειμενική συνάρτηση με συντελεστή για κάθε μεταβλητή το , όπου αυθαίρετα πολύ μεγάλος θετικός αριθμός. Η λύση του αναθεωρημένου προβλήματος πρέπει να είναι της μορφής , όπου οι λύσεις των μεταβλητών του αρχικού προβλήματος και όπου οι λύσεις των τεχνητών μεταβλητών οι οποίες πρέπει να είναι 0.

Παράδειγμα 4.5

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

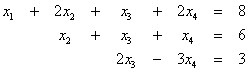
και

Το πρόβλημα γραμμικού προγραμματισμού είναι στην τυπική μορφή, δηλαδή, είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών είναι θετικά, έχει μόνο ισότητες και όλες οι μεταβλητές είναι θετικές.

Ο πίνακας του προβλήματος είναι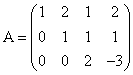

Παρατηρούμε ότι δεν περιέχεται ο μοναδιαίος πίνακας μέσα στον πίνακα Α. Επομένως θα εισάγουμε 2 τεχνητές μεταβλητές για να δημιουργήσουμε τον μοναδιαίο πίνακα.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

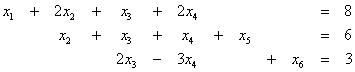
και και το Μ μεγάλος θετικός αριθμός.

Το αρχικό Simplex tableau είναι:

			2	-3	1	2	-Μ	-Μ
B		β							θ
	2	8	1	2	1	2	0	0	8
	-Μ	6	0	1	1	1	1	0	6
	-Μ	3	0	0	2	-3	0	1
	Z		2				0	0

Έχουμε και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			2	-3	1	2	-Μ
B		β						θ
	2		1	2	0		0
	-Μ		0	1	0		1
	1		0	0	1		0	--
	z		0		0		0

Έχουμε και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			2	-3	1	2
B		β					θ
	2		1		0	0
	2		0		0	1
	1		0		1	0
	z		0		0	0

και επειδή όλες οι ποσότητες είναι θετικές ή μηδέν και δεν υπάρχει τεχνητή μεταβλητή στην βάση, αυτό είναι το τελικό Simplex tableau.

Επομένως η άριστη λύση του προβλήματος με τις τεχνητές μεταβλητές (αναθεωρημένο πρόβλημα) είναι άριστη και του αρχικού.

Η λύση είναι με τιμή της αντικειμενικής συνάρτησης .

4.6 ΜΕΘΟΔΟΣ ΤΩΝ ΔΥΟ ΦΑΣΕΩΝ

Μεγάλο μειονέκτημα της Μ-μεθόδου ο μη καθορισμός του πόσο μεγάλο πρέπει να είναι το Μ, όταν χρησιμοποιούμε ηλεκτρονικό υπολογιστή. Επιλεγούμε το Μ αυθαίρετα μεγάλο το οποίο όμως μπορεί να προκαλέσει προβλήματα ακρίβειας στην υπολογιστική μηχανή (σφάλματα στρογγυλοποίησης). Τα προβλήματα αυτά μπορούμε να τα αποφύγουμε με την μέθοδο των 2 φάσεων.

Στην πρώτη φάση εισάγουμε τις τεχνητές μεταβλητές που χρειάζονται για να δημιουργηθεί ο μοναδιαίος πίνακας. Λύνουμε το βοηθητικό πρόβλημα το οποίο θέλουμε να έχει άριστη λύση μηδέν, δηλαδή, όλες οι τεχνητές να είναι μηδέν. Το σύνολο των άλλων μεταβλητών σε αυτή την περίπτωση αποτελούν βασική εφικτή λύση για το αρχικό πρόβλημα. Αν το βοηθητικό πρόβλημα έχει άριστη λύση θετική, τότε το αρχικό πρόβλημα δεν έχει εφικτή λύση.

Στην δεύτερη φάση λύνουμε το αρχικό πρόβλημα χρησιμοποιώντας σαν αρχική βασική εφικτή λύση του προβλήματος την άριστη λύση της 1^ης φάσης.

Παράδειγμα 4.6

Να λυθεί το παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

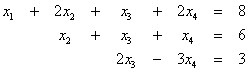
και

Είναι το ίδιο με το παράδειγμα 4.6

Το πρόβλημα γραμμικού προγραμματισμού είναι στην τυπική μορφή, δηλαδή, είναι πρόβλημα μεγιστοποίησης, τα δεξιά μέλη των περιορισμών είναι θετικά, έχει μόνο ισότητες και όλες οι μεταβλητές είναι θετικές.

Ο πίνακας του προβλήματος είναι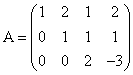

Παρατηρούμε ότι δεν περιέχεται ο μοναδιαίος πίνακας μέσα στον πίνακα Α. Επομένως θα εισάγουμε 2 τεχνητές μεταβλητές για να δημιουργήσουμε τον μοναδιαίο πίνακα.

Το πρόβλημα θα πάρει την εξής μορφή:

με περιορισμούς

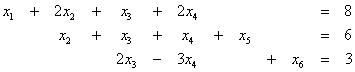
και .

Στην πρώτη φάση λύνουμε το πρόβλημα ή ισοδύναμα

Το αρχικό Simplex tableau είναι:

			0	0	0	0	-1	-1
B		β							θ
	2	8	1	2	1	2	0	0	8
	-1	6	0	1	1	1	1	0	6
	-1	3	0	0	2	-3	0	1
	Z	-9	0	-1	-3	2	0	0

Έχουμε και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			0	0	0	0	-1
B		β						θ
	0		1	2	0		0
	-1		0	1	0		1
	0		0	0	1		0	--
	z		0	-1	0		0

Έχουμε και , και επειδή , εισερχόμενη μεταβλητή είναι η , ενώ επειδή εξερχόμενη η , πιλότος το .

Το νέο Simplex tableau διαμορφώνεται ως εξής:

			0	0	0	0
B		β					θ
	0		1		0	0
	0		0		0	1
	0		0		1	0
	z	0	0	0	0	0

και επειδή όλες οι ποσότητες είναι θετικές ή μηδέν και δεν υπάρχει τεχνητή μεταβλητή στην βάση, αυτό είναι το τελικό Simplex tableau.

Επομένως η άριστη λύση του προβλήματος είναι με τιμή της αντικειμενικής συνάρτησης μηδέν.

Στην δεύτερη φάση λύνουμε το αρχικό πρόβλημα ξεκινώντας με το τελικό Simplex tableau της πρώτης φάσης με αντικειμενικούς συντελεστές τα αρχικά και υπολογίζουμε εκ’νέου τις ποσότητες .

Το αρχικό Simplex tableau της δεύτερης φάσης διαμορφώνεται ως εξής:

			2	-3	1	2
B		β					θ
	2		1		0	0
	2		0		0	1
	1		0		1	0
	z		0		0	0

και επειδή όλες οι ποσότητες είναι θετικές ή μηδέν, αυτό είναι το τελικό Simplex tableau της δεύτερης φάσης.

Επομένως η άριστη λύση του προβλήματος είναι με τιμή της αντικειμενικής συνάρτησης .

4.7 ΑΝΑΛΥΣΗ ΕΥΑΙΣΘΗΣΙΑΣ

Η ανάλυση ευαισθησίας είναι μία μέθοδος η οποία εφαρμόζεται για να προσδιορίσει την ευαισθησία της λύσης ενός προβλήματος γραμμικού προγραμματισμού στις μεταβολές των παραμέτρων του. Συγκεκριμένα το Simplex tableau της άριστης λύσης μας δίνει πληροφορίες που αφορούν

1) την άριστη λύση του προβλήματος γραμμικού προγραμματισμού

2) το διαχωρισμό των περιορισμών σε δεσμευτικούς ή χαλαρούς

3) τις δυϊκές τιμές

4) το εύρος αριστότητας των αντικειμενικών συντελεστών, δηλαδή, την αλλαγή που μπορούμε να κάνουμε σε ένα αντικειμενικό συντελεστή χωρίς να αλλάξει η άριστη λύση

5) το εύρος εφικτότητας των δεξιών μελών των περιορισμών, δηλαδή, την αλλαγή που μπορούμε να κάνουμε σε ένα δεξιό μέλος περιορισμού χωρίς να αλλάξει η εφικτή περιοχή ή χωρίς να αλλάξει η δυϊκή τιμή του περιορισμού.

Παράδειγμα 4.7

Να βρεθούν ποιοι περιορισμοί είναι χαλαροί και ποιοι δεσμευτικοί, οι δυϊκές τιμές, το εύρος αριστότητας για κάθε αντικειμενικό συντελεστή και το εύρος εφικτότητας για κάθε δεξιό μέλος περιορισμού (σταθερού όρου) στο παρακάτω πρόβλημα γραμμικού προγραμματισμού:

με περιορισμούς

και

Όπως είδαμε στο παράδειγμα 4.1 το παραπάνω πρόβλημα γραμμικού προγραμματισμού έχει τελικό Simplex tableau το εξής:

			3	8	0	0
B		β					θ
	8	4	0	1	1	-1
	3	12	1	0	-2	3
	Z	68	0	0	2	1

Η άριστη (βέλτιστη) λύση είναι με τιμή της αντικειμενικής συνάρτησης .

Η άριστη λύση για όλες τις μεταβλητές του προβλήματος είναι . Η περιθώρια μεταβλητή που αντιστοιχεί στον πρώτο περιορισμό έχει τιμή μηδέν, άρα ο πρώτος περιορισμός είναι δεσμευτικός. Η περιθώρια μεταβλητή που αντιστοιχεί στον δεύτερο περιορισμό έχει τιμή μηδέν, άρα ο και δεύτερος περιορισμός είναι δεσμευτικός.

Οι δυϊκές τιμές των περιορισμών στο τελικό Simplex tableau είναι οι ποσότητες που έχουν οι αντίστοιχες περιθώριες μεταβλητές. Ο πρώτος περιορισμός έχει περιθώρια μεταβλητή την , άρα η δυϊκή του τιμή είναι . Ο δεύτερος περιορισμός έχει περιθώρια μεταβλητή την , άρα η δυϊκή του τιμή είναι .

Για να βρούμε το εύρος αριστότητας ενός αντικειμενικού συντελεστή χρησιμοποιούμε την σχέση με την γραμμή της αντίστοιχης μεταβλητής και η μεταβολή που γίνεται στον αντικειμενικό συντελεστή. Άρα για τον θα ισχύει , δηλαδή, . Περιοριζόμαστε μόνο στις μη βασικές μεταβλητές και έχουμε και πρέπει να ισχύει , άρα 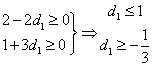, δηλαδή, .

Για τον θα ισχύει , δηλαδή, . Περιοριζόμαστε μόνο στις μη βασικές μεταβλητές και έχουμε και πρέπει να ισχύει , άρα 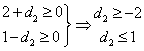, δηλαδή, .

Για να βρούμε το εύρος εφικτότητας ενός δεξιού μέλους περιορισμού χρησιμοποιούμε την σχέση με την στήλη της αντίστοιχης περιθώριας μεταβλητής και η μεταβολή που γίνεται στο δεξιό μέλος περιορισμού. Άρα για τον θα ισχύει , δηλαδή, . Πρέπει να ισχύει , άρα 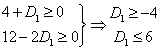, δηλαδή, .

Για τον θα ισχύει , δηλαδή, . Πρέπει να ισχύει , άρα 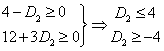, δηλαδή, .