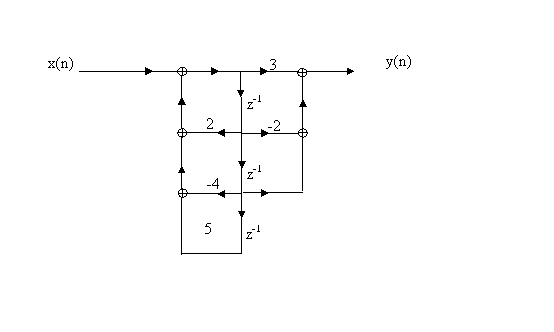ΠΕΡΙΕΧΟΜΕΝΑ
1. Κεφάλαιο 1 - Εισαγωγή
2. Κεφάλαιο 2 - Διακριτά σήματα και συστήματα
2.1. Διακριτά σήματα.
2.1.1. Θεμελιώδη διακριτά σήμα.
2.1.2. Διάρκεια διακριτού σήματος
2.1.3. Περιοδικότητα διακριτού σήματος
2.1.4. Συμμετρικά σήματα
2.1.5. Αντιστροφή, ολίσθηση και κλιμάκωση σήματος
2.1.6. Πράξεις διακριτών σημάτων
2.1.7. Ανάλυση διακριτού σήματος σε διακριτές κρουστικές ώσεις
2.2. Διακριτά συστήματα
2.2.1. Διασύνδεση συστημάτων
2.2.2. Μνήμη διακριτού συστήματος
2.2.3. Αμεταβλητότητα κατά τη μετατόπιση
2.2.4. Γραμμικότητα
2.2.5. Αιτιότητα
2.2.6. Ευστάθεια φραγμένης εισόδου-φραγμένης εξόδου
2.2.7. Αντιστρέψιμα συστήματα
2.2.8. Απόκριση συστήματος σε κρουστική διέγερση, το συνελικτικό άθροισμα
2.2.9. Ιδιότητες της συνέλιξης διακριτών σημάτων
2.2.10. Τρόποι υπολογισμού της συνέλιξης διακριτών σημάτων
3. Κεφάλαιο 3 –Περί μετασχηματισμών σημάτων διακριτού χρόνου.
3.1 Εισαγωγή
3.2 Ερμηνεία μετασχηματισμών με διανυσματική ανάλυση
3.3 Ερμηνεία μετασχηματισμών με γραμμική άλγεβρα
3.4 Ο διακριτός μετασχηματισμός συνημιτόνου (DCT: Discrete Cosine Transform)
3.4.1 Ο δισδιάστατος (2Δ) διακριτός μετασχηματισμός συνημιτόνου
(2D-DCT: Discrete Cosine Transform)
3.5 Ερμηνεία και υπολογισμοί μετασχηματισμών μιγαδικών σημάτων διακριτού χρόνου.
4. Κεφάλαιο 4 – Ο μετασχηματισμός Fourier
4.1 Εισαγωγή
4.2 Ο διακριτός μετασχηματισμός Fourier N-σημείων
4.3 Ο μετασχηματισμός Fourier διακριτού χρόνου.
4.3.1 Ιδιότητες του μετασχηματισμού Fourier διακριτού χρόνου
4.4 Σχέση της συνέλιξης με το μετασχηματισμό και τον διακριτό μετασχηματισμό
Fourier.
5. Κεφάλαιο 5 - Ανάλυση σημάτων και συστημάτων με τον μετασχηματισμό Fourier
5.1 Εισαγωγή.
5.2 Απόκριση συχνότητας.
5.2.1 Φίλτρα επιλογής συχνοτήτων
5.3 Ανάλυση της δειγματοληψίας.
6. Κεφάλαιο 6 – Ο μετασχηματισμός Ζ
6.1 Εισαγωγή
6.2 Ορισμός του μετασχηματισμού Ζ
6.2.1 Ιδιότητες του μετασχηματισμού Ζ
6.2.2 Ο αντίστροφος μετασχηματισμός Ζ, ανάλυση σε μερικά κλάσματα
6.3 Ο Μονόπλευρος μετασχηματισμό Ζ
7. Κεφάλαιο 7 - Ανάλυση συστημάτων με τον μετασχηματισμό Z
7.1 Εισαγωγή.
7.2 Συνάρτηση μεταφοράς.
7.3 Έλεγχος ευστάθειας και αιτιότητας LTI συστήματος
7.4 Υπολογισμός της εξόδου συστήματος LTI.
8. Κεφάλαιο 8 – Υλοποίηση συστημάτων διακριτού χρόνου
8.1 Εισαγωγή.
8.2 Ψηφιακά δικτυώματα
8.3 Περιγραφή συστημάτων FIR
8.4 Περιγραφή συστημάτων IIR
ΚΕΦΑΛΑΙΟ 1
Η επεξεργασία ψηφιακού σήματος είναι ένας τομέας της επιστήμης και της εφαρμοσμένης μηχανικής που έχει αναπτυχθεί γρήγορα κατά τη διάρκεια των προηγούμενων 30 ετών. Αυτή η γρήγορη ανάπτυξη είναι αποτέλεσμα των σημαντικών πλεονεκτημάτων της τεχνολογίας των ψηφιακών υπολογιστών και της βιομηχανίας των ολοκληρωμένων κυκλωμάτων. Οι ψηφιακοί υπολογιστές και τα ψηφιακά κυκλώματα πριν τρεις δεκαετίες ήταν σχετικά ογκώδη και ακριβά και κατά συνέπεια η χρήση τους περιορίστηκε σε επιστημονικούς υπολογισμούς και εφαρμογές γενικής χρήσης, χωρίς απαιτήσεις εκτέλεσης σε πραγματικό χρόνο. Η γρήγορη ανάπτυξη στην τεχνολογία ολοκληρωμένων κυκλωμάτων που άρχισε από την μέση κλίμακα ολοκλήρωσης (Medium Scale Integration) και εξελίχθηκε στην μεγάλη (Large Scale Integration), και τώρα την πολύ μεγάλη κλίμακα ολοκλήρωσης (Very Large Scale Integration) των ηλεκτρονικών κυκλωμάτων έχει οδηγήσει στην ανάπτυξη πιο ισχυρών, μικρότερων, γρηγορότερων και φτηνότερων ψηφιακών υπολογιστών και ειδικευμένου ψηφιακού εξοπλισμού. Αυτά τα φθηνά και σχετικά γρήγορα ψηφιακά κυκλώματα κατέστησαν δυνατόν να κατασκευαστούν ιδιαίτερα περίπλοκα ψηφιακά συστήματα ικανά να εκτελέσουν σύνθετες λειτουργίες επεξεργασίας ψηφιακού σήματος που είναι συνήθως δύσκολο ή/και πάρα πολύ ακριβό να εκτελεστούν για αναλογικά σήματα με συστήματα αναλογικών κυκλωμάτων. Ως εκ τούτου πολλοί από τους στόχους επεξεργασίας σήματος που εκτελέστηκαν συμβατικά με τα αναλογικά μέσα πραγματοποιούνται σήμερα από λιγότερο ακριβό και συχνά πιο αξιόπιστο ψηφιακό υλικό. Αυτό δεν σημαίνει ότι η επεξεργασία ψηφιακού σήματος είναι η κατάλληλη λύση για όλα τα προβλήματα επεξεργασίας σήματος.. Για σήματα με εξαιρετικά μεγάλο εύρος ζώνης όπου απαιτείται η επεξεργασία σε πραγματικό χρόνο, η αναλογική επεξεργασία ή η επεξεργασία οπτικού σήματος είναι η ίσως η μόνη πιθανή λύση. Εντούτοις, όπου τα ψηφιακά κυκλώματα είναι διαθέσιμα και προσφέρουν ικανοποιητική ταχύτητα προτιμώνται διότι είναι φτηνότερα και τα συστήματα πιο αξιόπιστα και παραμετροποιήσιμα. Ειδικότερα, το υλικό ψηφιακής επεξεργασίας επιτρέπει την ενσωμάτωση λογισμικού που μπορεί να τροποποιήσει ευκολότερα τις λειτουργίες επεξεργασίας σήματος που εκτελούνται. Κατά συνέπεια το ψηφιακό υλικό και το σχετικό λογισμικό παρέχουν έναν μεγαλύτερο βαθμό ευελιξίας στο σχεδιασμό των συστημάτων. Επίσης επιτυγχάνεται συχνά ακρίβεια μεγαλύτερης τάξης με το ψηφιακό υλικό και το λογισμικό έναντι των αναλογικών κυκλωμάτων και των συστημάτων επεξεργασίας αναλογικού σήματος. Για όλους αυτούς τους λόγους, υπήρξε μια εκρηκτική αύξηση της θεωρίας επεξεργασίας ψηφιακού σήματος και των εφαρμογών της κατά τη διάρκεια των τελευταίων δεκαετιών.
ΚΕΦΑΛΑΙΟ 2
Διακριτό
σήμα ή σήμα διακριτού χρόνου
ονομάζουμε μία ακολουθία πραγματικών ή μιγαδικών τιμών x(n), ![]() και
και ![]() . Το διακριτό σήμα είναι δηλαδή μία συνάρτηση της οποίας η
ανεξάρτητη μεταβλητή είναι ακέραιος αριθμός. Στην ΨΕΣ η ανεξάρτητη μεταβλητή n ονομάζεται και «χρόνος» αν και
μπορεί να παριστάνει συντεταγμένες χώρου, αύξοντες αριθμούς κ.α. Ένα διακριτό
σήμα δεν ορίζεται για τιμές του n που
δεν είναι ακέραιες. H
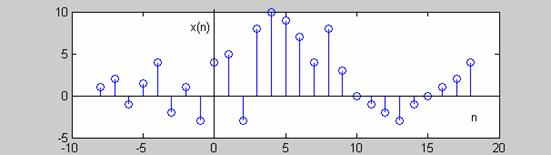
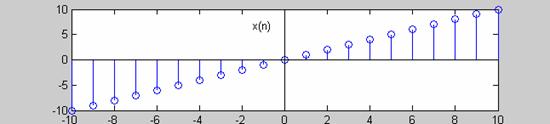
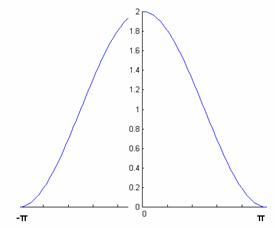
γραφική παράσταση ενός διακριτού σήματος έχει την μορφή που δείχνεται στο
Σχ.2.1.1
. Το διακριτό σήμα είναι δηλαδή μία συνάρτηση της οποίας η
ανεξάρτητη μεταβλητή είναι ακέραιος αριθμός. Στην ΨΕΣ η ανεξάρτητη μεταβλητή n ονομάζεται και «χρόνος» αν και
μπορεί να παριστάνει συντεταγμένες χώρου, αύξοντες αριθμούς κ.α. Ένα διακριτό
σήμα δεν ορίζεται για τιμές του n που
δεν είναι ακέραιες. H
γραφική παράσταση ενός διακριτού σήματος έχει την μορφή που δείχνεται στο
Σχ.2.1.1
|
|
|
Σχήμα 2.1.1 |
Τα διακριτά σήματα προέρχονται από α) μεγέθη που από τη φύση τους είναι αριθμήσιμα, π.χ. έσοδα ανά ημέρα, κίνηση ανά ώρα, β) μεγέθη που μεταβάλλονται σε σχέση με μία συνεχή μεταβλητή (συνεχή σήματα) ύστερα από μία διαδικασία δειγματοληψίας. Ο πιο συνήθης τρόπος μετατροπής ενός αναλογικού σήματος σε διακριτό είναι η περιοδική ή ομοιόμορφη δειγματοληψία. Λαμβάνονται δείγματα του σήματος σε διαδοχικές τιμές της ανεξάρτητης μεταβλητής. Αν η απόσταση δύο διαδοχικών τιμών είναι σταθερή ίση με Τs και xa(t) η συνάρτηση της συνεχούς μεταβλητής t, το διακριτό σήμα x(n) προκύπτει από τη σχέση
![]() (2.1.1)
(2.1.1)
Η ποσότητα
![]() λέγεται ρυθμός
δειγματοληψίας. Η επιλογή κατάλληλης τιμής του ρυθμού δειγματοληψίας θα
εξετασθεί αργότερα στο σχετικό κεφάλαιο.
λέγεται ρυθμός
δειγματοληψίας. Η επιλογή κατάλληλης τιμής του ρυθμού δειγματοληψίας θα
εξετασθεί αργότερα στο σχετικό κεφάλαιο.
Αν ένα συνεχές ή διακριτό σήμα παίρνει τιμές από ένα πεπερασμένου πλήθους σύνολο τιμών, τότε λέγεται σήμα διακριτών τιμών. Μ’ άλλα λόγια το πεδίο τιμών του σήματος είναι ένα σύνολο πεπερασμένου πλήθους στοιχείων. Ένα διακριτό σήμα διακριτών τιμών λέγεται ψηφιακό. Ένα ψηφιακό σήμα πεπερασμένου μήκους μπορεί να αποθηκευτεί στη μνήμη ενός ψηφιακού υπολογιστή με ακρίβεια όση η μικρότερη απόσταση που υπάρχει μεταξύ των τιμών του. Η ψηφιοποίηση μη ψηφιακών σημάτων απαιτεί την δειγματοληψία του πεδίου ορισμού τους και τον κβαντισμό του πεδίου τιμών τους όπως θα δούμε σε επόμενο κεφάλαιο.
2.1.1. Θεμελιώδη διακριτά σήματα
Ακολούθως
θα αναφέρουμε μερικά διακριτά σήματα που χρησιμοποιούνται ευρέως στην ψηφιακή
επεξεργασία σημάτων. Τέτοια είναι η διακριτή
κρουστική ώση, η βηματική ακολουθία,
η εκθετική ακολουθία, η μιγαδική ακολουθία, η μοναδιαία γραμμική ακολουθία.
Η διακριτή συνάρτηση δέλτα ή διακριτή κρουστική ώση συμβολίζεται δ(n) και ορίζεται από τη σχέση
![]() (2.1.1.1)
(2.1.1.1)
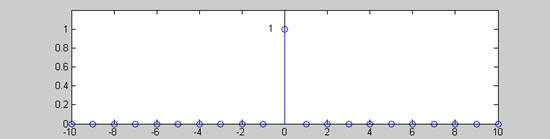
Η γραφική της παράσταση φαίνεται στο Σχ.2.1.1.1.
|
|
|
Σχήμα 2.1.1.1. Η διακριτή κρουστική ώση δ(n). |
Η βηματική ακολουθία συμβολίζεται u(n) και ορίζεται από τη σχέση
![]() (2.1.1.2)
(2.1.1.2)
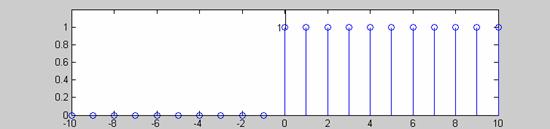
Η γραφική της παράσταση φαίνεται στο Σχ.2.1.1.2.
|
|
|
Σχήμα 2.1.1.2. Η βηματική ακολουθία u(n). |
Η εκθετική ακολουθία ορίζεται από τη σχέση
![]() ,
, ![]() (2.1.1.3)
(2.1.1.3)
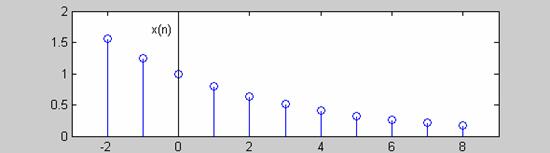
Η γραφική της παράσταση για διαφορετικές τιμές του α, φαίνεται στο Σχ.2.1.1.3.
|
|
|
(α) Η εκθετική ακολουθία για α=0.8. |
|
|
|
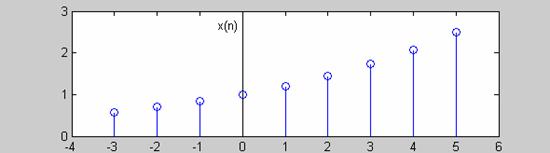
(β) Η εκθετική ακολουθία για α=1.2. |
|
|
|
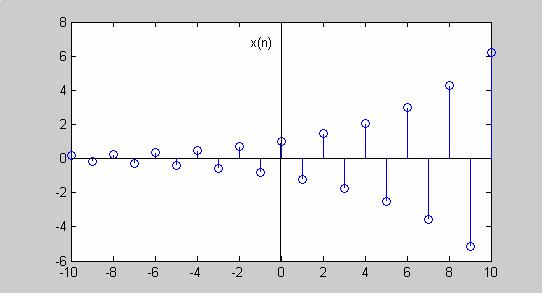
(β) Η εκθετική ακολουθία για α=-1.2. |
|
Σχήμα 2.1.1.3 |
Ιδιαίτερο
ενδιαφέρον παρουσιάζει η εκθετική ακολουθία όταν ![]() ,
, ![]() . Τότε ονομάζεται μιγαδική εκθετική ακολουθία και βάσει της
ταυτότητας του Euler ισχύει η σχέση
. Τότε ονομάζεται μιγαδική εκθετική ακολουθία και βάσει της
ταυτότητας του Euler ισχύει η σχέση
![]() (2.1.1.4)
(2.1.1.4)
Η μιγαδικές εκθετικές ακολουθίες είναι η βάση της ανάλυσης Fourier που θα παρουσιάσουμε σε ακόλουθο κεφάλαιο.
2.1.2.
Διάρκεια διακριτού σήματος..
Ένα διακριτό σήμα λέγεται πεπερασμένου μήκους αν οι τιμές του μηδενίζονται για κάθε τιμή του n που δεν ανήκει σε ένα πεπερασμένο διάστημα [L,R], αν δηλαδή ικανοποιείται η σχέση
![]() (2.1.2.1)
(2.1.2.1)
Στις πλείστες των περιπτώσεων x(L), x(R) έχουν μη μηδενικές τιμές. Η έκταση N του διαστήματος [L,R] λέγεται μήκος του σήματος και είναι
Ν=R-L+1 (2.1.2.2)
Σήματα που δεν είναι πεπερασμένου μήκους ονομάζονται απείρου μήκους. Ένα διακριτό σήμα απείρου μήκους λέγεται σήμα δεξιάς πλευράς αν ικανοποιεί τη σχέση
![]() (2.1.2.3)
(2.1.2.3)
και αριστερής πλευράς αν
![]() (2.1.2.4)
(2.1.2.4)
Τέλος, αν ένα διακριτό σήμα απείρου μήκους δεν είναι δεξιάς ή αριστερής πλευράς λέγεται αμφίπλευρο.
Τα πεπερασμένα μήκους σήματα και τα σήματα δεξιάς ή αριστερής πλευράς μπορούν να περιγραφούν αλγεβρικά με κατάλληλη χρήση διακριτών βηματικών ακολουθιών. Αν x(n) σήμα απείρου μήκους τότε μπορεί να ορισθεί το πεπερασμένου μήκος σήμα y(n) στο διάστημα [L,R] ως εξής
![]() (2.1.2.5)
(2.1.2.5)
ή
![]() (2.1.2.6)
(2.1.2.6)
Το σήμα
![]() (2.1.2.7)
(2.1.2.7)
είναι δεξιάς
πλευράς με ![]()
2.1.3. Περιοδικότητα διακριτού σήματος
Ένα σήμα λέγεται περιοδικό αν υπάρχει θετικός ακέραιος Ν ώστε
![]() (2.1.3.1)
(2.1.3.1)
Ο ακέραιος Ν λέγεται περίοδος του σήματος. Είναι προφανές ότι αν Ν η περίοδος του σήματος, τότε οι τιμές 2Ν, 3Ν και κάθε θετικό ακέραιο πολλαπλάσιο του Ν είναι περίοδοι του σήματος. Η μικρότερη τιμή της περιόδου ονομάζεται πρωτεύουσα περίοδος. Αν δεν υπάρχει θετικός ακέραιος Ν ώστε να ισχύει η σχέση (2.1.3.1), το σήμα λέγεται μη περιοδικό. Παράδειγμα περιοδικού διακριτού σήματος είναι το σήμα
![]() με περίοδο Ν=5 (2.1.3.2.)
με περίοδο Ν=5 (2.1.3.2.)
Παράδειγμα μη περιοδικού σήματος είναι το
![]() (2.1.3.3)
(2.1.3.3)
Ένα πραγματικό διακριτό σήμα x(n) λέγεται άρτιο αν ισχύει η σχέση
![]() (2.1.4.1)
(2.1.4.1)
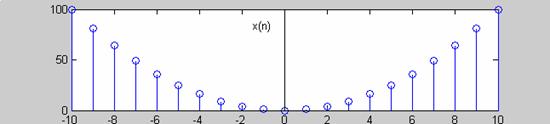
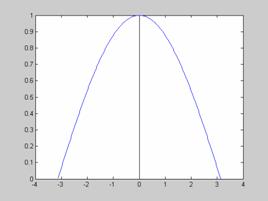
Η γραφική παράσταση ενός άρτιου σήματος παρουσιάζει αξονική συμμετρία ως προς τον κάθετο άξονα. Για παράδειγμα το σήμα x(n)=n2 είναι άρτιο με γραφική παράσταση όπως φαίνεται στο Σχ. 2.1.4.1.
|
|
|
Σχήμα 2.1.4.1. |
.
Ένα πραγματικό διακριτό σήμα x(n) λέγεται περιττό αν ισχύει η σχέση
![]() (2.1.4.2)
(2.1.4.2)
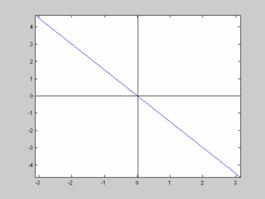
Η γραφική παράσταση ενός περιττού σήματος παρουσιάζει κεντρική συμμετρία ως προς την αρχή των αξόνων. Για παράδειγμα το σήμα x(n)=n είναι περιττό με γραφική παράσταση όπως φαίνεται στο Σχ. 2.1.4.2.
|
|
|
Σχήμα 2.1.4.2. |
Κάθε πραγματικό σήμα μπορεί να γραφεί σαν άθροισμα ενός άρτιου και ενός περιττού σήματος. Πράγματι αν xα(n) άρτιο και xπ(n) περιττό σήμα θα πρέπει να ισχύουν οι σχέσεις
![]() (2.1.4.3)
(2.1.4.3) ![]() (2.1.4.4)
(2.1.4.4)
Από την πρόσθεση των (2.1.4.3) και (2.1.4.4) προκύπτει ότι
![]() (2.1.4.6)
(2.1.4.6)
Από την αφαίρεση των (2.1.4.3) και (2.1.4.4) προκύπτει ότι
![]() (2.1.4.7)
(2.1.4.7)
Ένα μιγαδικό διακριτό σήμα x(n) λέγεται συζυγές συμμετρικό αν ισχύει η σχέση
![]() (2.1.4.8)
(2.1.4.8)
Ένα μιγαδικό διακριτό σήμα x(n) λέγεται συζυγές αντισυμμετρικό αν ισχύει η σχέση
![]() (2.1.4.9)
(2.1.4.9)
Κάθε μιγαδικό σήμα μπορεί να γραφεί σαν άθροισμα ενός συζυγούς συμμετρικού και ενός συζυγούς αντισυμμετρικού σήματος. Η απόδειξη αφήνεται ως άσκηση στον αναγνώστη.
2.1.5. Αντιστροφή, ολίσθηση και κλιμάκωση σήματος
Εάν σε ένα σήμα x(n) εφαρμοσθεί ένας μετασχηματισμός στην ανεξάρτητη μεταβλητή n, ![]() , προκύπτει το σήμα x(f(n)). Αν f(n)=-n τότε λέμε ότι το σήμα έχει υποστεί αντιστροφή
και μετασχηματίζεται στο σήμα
, προκύπτει το σήμα x(f(n)). Αν f(n)=-n τότε λέμε ότι το σήμα έχει υποστεί αντιστροφή
και μετασχηματίζεται στο σήμα
y(n)=x(-n). (2.1.5.1)
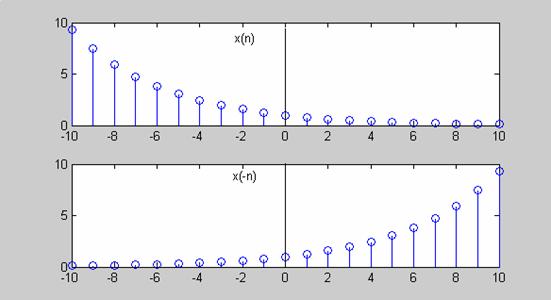
Η γραφική παράσταση του x(-n) είναι συμμετρική ως προς
τον κάθετο άξονα με αυτήν του x(n) (Σχ.2.1.5.1).
Αν f(n)=n-n0, τότε λέμε ότι το σήμα έχει υποστεί μετατόπιση ή ολίσθηση κατά n0 και μετασχηματίζεται στο σήμα
y(n)= x(n-n0). (2.1.5.2)
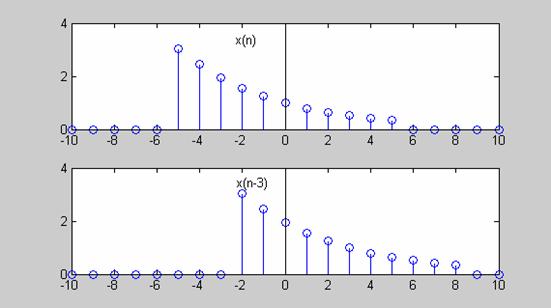
Η γραφική παράσταση του x(n-n0) επροκύπτει με μετατόπιση της γραφικής παράστασης του x(n) κατά n0, στον οριζόντιο άξονα (Σχ.2.1.5.2).
Γενικά, αν εφαρμοσθεί ολίσθηση ενός σήματος και ακολούθως αντιστροφή
του, προκύπτει διαφορετικό αποτέλεσμα από ότι θα προέκυπτε από την
εφαρμογή πρώτα αντιστροφής του και
ακολούθως ολίσθησης. Αυτό φαίνεται από ακόλουθες σχέσεις
![]() (2.1.5.3)
(2.1.5.3)
![]() (2.1.5.4)
(2.1.5.4)
Το αποτέλεσμα θα ήταν ίδιο
αν η ολίσθηση σε μία από τις δύο διαδικασίες γίνει κατά –n0.
|
|
|
Σχήμα 2.1.5.1 |
|
|
|
Σχήμα 2.1.5.2. |
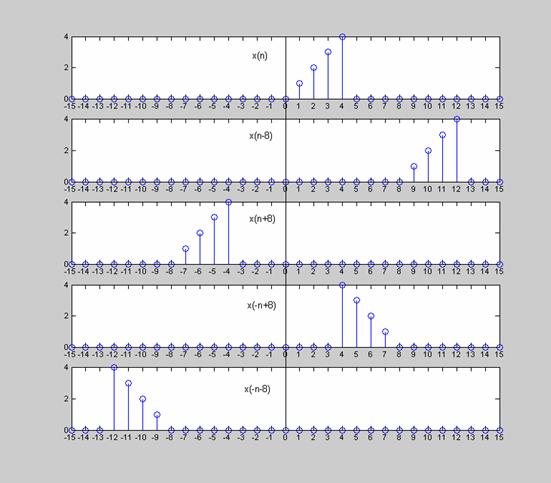
Τελικά με τις πράξεις τις ολίσθησης και της
αντιστροφής από το αρχικό σήμα x(n) προκύπτουν τα σήματα x(n-n0), x(n+n0), x(-n+n0), x(-n-n0). Στο Σχ.(2.1.5.3)
δείχνεται ένα παράδειγμα των γραφικών παραστάσεων των σημάτων αυτών σε σχέση με
την γραφική παράσταση του x(n).
Κλιμάκωση
υφίσταται ένα σήμα αν f(n)=Μn ή f(n)=n/Μ, όπου Μ ακέραιος. Στην πρώτη περίπτωση το διακριτό σήμα λέμε ότι υπέστη υποδειγματοληψία και στη δεύτερη υπερδειγματοληψία. Κατά την
υποδειγματοληψία προκύπτει το σήμα
y(n)= x(Mn) (2.1.5.5)
και κατά την
υπερδειγματοληψία το σήμα
y(n)= x(n/Μ) αν ![]() (2.1.5.6)
(2.1.5.6)
Για τις μη ακέραιες τιμές
του πηλίκου n/M το σήμα x(n/M) δεν ορίζεται.
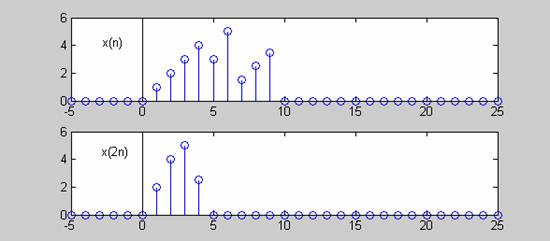
Στο Σχ.2.1.5.4. δείχνεται η
γραφική παράσταση υποδειγματοληψίας ενός σήματος.
|
|
|
Σχήμα 2.1.5.3 |
|
|
|
Σχήμα 2.1.5.4 |
2.1.6. Πράξεις διακριτών σημάτων.
Μεταξύ των ακολουθιών δύο διακριτών σημάτων μπορούν να εκτελεστούν
οι βασικές πράξεις μεταξύ των τιμών τους που αντιστοιχούν στην ίδια τιμή της
ανεξάρτητης μεταβλητής και να προκύψει μία νέα ακολουθία που λέμε ότι είναι το
αποτέλεσμα της πράξης μεταξύ των δύο αρχικών ακολουθιών. Έτσι ορίζονται οι
πράξεις που φαίνονται στον ακόλουθο πίνακα
|
Πρόσθεση |
x(n)+ y(n) |
|
Αφαίρεση |
x(n)- y(n) |
|
Πολλαπλασιασμός |
x(n)* y(n) |
|
Διαίρεση |
x(n)/ y(n)
|
|
Πίνακας 2.1.6.1. |
|
2.1.7. Ανάλυση διακριτού σήματος σε διακριτές κρουστικές ώσεις
Η διακριτή ώση δ(n) μπορεί να χρησιμοποιηθεί για την περιγραφή ενός διακριτού σήματος σύμφωνα με τη σχέση
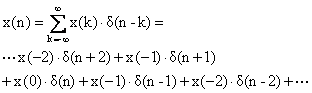 (2.1.7.1)
(2.1.7.1)
Από την παραπάνω σχέση μπορούμε να περάσουμε σε διανυσματική ερμηνεία των διακριτών σημάτων και της κρουστικής ώσης. Ας θεωρήσουμε το πεπερασμένου μήκους σήμα x(n) με μήκος Ν=3, n=0,1,2 (Lx=0, Rx=2) και την διανυσματική περιγραφή του με τον πίνακα στήλης
x=[x(0), x(1), x(2)]T. (2.1.7.2)
Σύμφωνα με την σχέση (2.1.7.1)
![]() (2.1.7.3)
(2.1.7.3)
Για n=0,1,2 οι δ(n), δ(n-1), δ(n-2) περιγράφονται διανυσματικά από τους πίνακες στήλης ως εξής:
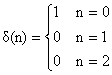 , ήτοι
διανυσματικά δ0=[1,0,0]Τ,
, ήτοι
διανυσματικά δ0=[1,0,0]Τ,
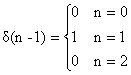 , ήτοι διανυσματικά δ1=[0,1,0]Τ,
(2.1.7.4)
, ήτοι διανυσματικά δ1=[0,1,0]Τ,
(2.1.7.4)
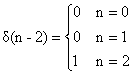 , ήτοι διανυσματικά δ2=[0,0,1]Τ
, ήτοι διανυσματικά δ2=[0,0,1]Τ
Από τις (2.1.7.2) και (2.1.7.4) οδηγούμαστε στην γραφή των ακόλουθων σχέσεων
 (2.1.7.5)
(2.1.7.5)
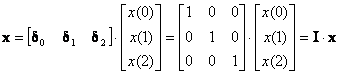 (2.1.7.6)
(2.1.7.6)
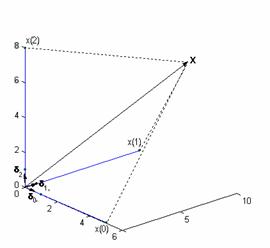
Διαπιστώνουμε ότι υπάρχει ομοιότητα των σχέσεων (2.1.7.3) και (2.1.7.5). Θεωρώντας τα δ0, δ1, δ2 ως τα μοναδιαία διανύσματα στον τρισδιάστατο Ευκλείδειο χώρο (Ε3), το πεπερασμένο διακριτό σήμα x(n) με μήκος Ν=3 αναπαρίσταται από το διάνυσμα x όπως φαίνεται στο Σχ.2.1.7.1.
|
|
|
Σχήμα 2.1.7.1. |
Οι συντεταγμένες του διανύσματος είναι οι προβολές του στα μοναδιαία διανύσματα δ0, δ1, δ2 και δίνονται από τις σχέσεις του εσωτερικού του γινομένου με αυτά ως ακολούθως
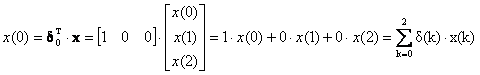 (2.1.7.7)
(2.1.7.7)
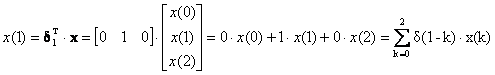 (2.1.7.8)
(2.1.7.8)
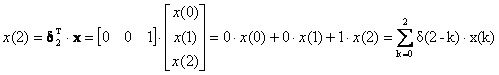 (2.1.7.9)
(2.1.7.9)
και γενικά για n=0,1,2
![]() (2.1.7.10)
(2.1.7.10)
Προέκυψε δηλαδή η σχέση (2.1.7.10) που είναι η ίδια με την (2.1.7.3)
Στο παράδειγμα αυτό το μήκος του διακριτού σήματος είναι Ν=3 και με αριστερό δείκτη Lx=0 και δεξιό Rx=2. Αν ο Lx πάρει οσοδήποτε μικρή τιμή και Rx οσοδήποτε μεγάλη μπορούμε πούμε ότι κάθε διακριτό σήμα είναι διάνυσμα σε ένα χώρο με οσοδήποτε μεγάλο πλήθος διαστάσεων (άπειρο πλήθος διαστάσεων) και συντεταγμένες (προβολές) στα μοναδιαία διανύσματα δ(n-k) τις τιμές x(n) όπως φαίνεται και από την (2.1.7.1). Ας σημειωθεί ακόμη ότι
![]() (2.7.1.11)
(2.7.1.11)
δηλαδή οι κρουστικές διακριτές ώσεις ως διανύσματα είναι κάθετα μεταξύ τους με μέτρο μονάδα. Αποτελούν δηλαδή μία ορθοκανονική βάση. Σε επόμενο κεφάλαιο θα αναφέρουμε και άλλες ορθοκανονικές και ορθομοναδιαίες βάσεις και θα δούμε την ανάλυση των διακριτών σημάτων σε αυτές. Η ανάλυση αυτή αφορά διάφορους μετασχηματισμούς όπως ο διακριτός μετασχηματισμός Fourier, ο μετασχηματισμός του συνημιτόνου κ.α.
Σε πολλές εφαρμογές από ένα διακριτό σήμα x(n) προκύπτει ένα διακριτό σήμα y(n) σύμφωνα με κάποιο αλγόριθμο (σαφές και πεπερασμένο σύνολο πράξεων ή εντολών ). Στη περίπτωση αυτή ο αλγόριθμος ονομάζεται διακριτό σύστημα. Το σήμα x(n) λέγεται σήμα εισόδου (input signal) ή σήμα διέγερσης (excitation signal) του συστήματος και το σύστημα y(n) σήμα εξόδου (output signal) ή σήμα απόκρισης (response signal) του συστήματος. Λέμε ακόμη ότι το σήμα x(n) μετασχηματίζεται στο σήμα y(n) και ονομάζουμε το σύστημα μετασχηματισμό (transformation) του x(n) στο y(n). Η γενική μαθηματική έκφραση για ένα σύστημα είναι
y(n)=T[x(n)] (2.2.1)
όπου το σύμβολο
Τ συμβολίζει το μετασχηματισμό και συχνά ονομάζεται τελεστής (operator). Το σύστημα λειτουργεί ως μία απεικόνιση των
τιμών του σήματος εισόδου στις τιμές του σήματος εξόδου. Η περιγραφή της
απεικόνισης μπορεί να γίνει ανάλογα με τη φύση της, με χρήση αλγεβρικών
παραστάσεων, πινάκων αντιστοίχησης (look up tables) ή εντολών. Ακολούθως αναφέρονται
χαρακτηριστικά για τον τρόπου ορισμού τους, παραδείγματα συστημάτων.
Α) αλγεβρικά:![]()
Β) Με πίνακα αντιστοίχησης
|
x(n) |
y(n) |
|
4 |
1 |
|
2 |
-1 |
|
-1 |
2.4 |
|
Αλλιώς |
0 |
Γ) Για x με μήκος Ν, το y αποτελείται από τις τιμές του x ταξινομημένες σε
φθίνουσα σειρά. (αλγόριθμος φθίνουσας ταξινόμησης).
Ένα
σύστημα διαγραμματικά παριστάνεται ως ακολούθως

ή
![]()
Όταν η έξοδος
ενός συστήματος αποτελεί είσοδο ενός άλλου το λέμε ότι τα δύο συστήματα είναι
συνδεδεμένα σε σειρά.(Σχ.2.2.1.1)
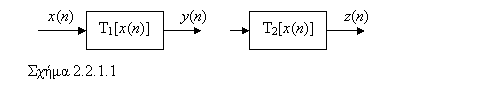
Όταν οι έξοδοι
δύο συστημάτων αθροιστούν τότε λέμε ότι έχουν συνδεθεί παράλληλα (Σχ.2.2.1.2)
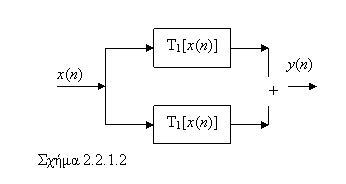
2.2.2. Μνήμη διακριτού συστήματος
Σύστημα χωρίς μνήμη λέγεται το σύστημα που για κάθε τιμή της ανεξάρτητης μεταβλητής n, η έξοδός του y(n) εξαρτάται μόνο από την αντίστοιχη τιμή της εισόδου x(n) και όχι από προηγούμενες ή επόμενες τιμές της n. Σε διαφορετική περίπτωση το σύστημα λέγεται σύστημα με μνήμη. Για παράδειγμα το σύστημα που δίνεται από τη σχέση
![]() (2.2.2.1)
(2.2.2.1)
είναι σύστημα χωρίς μνήμη. Αντίθετα τα συστήματα που δίνονται από τις σχέσεις
![]() (2.2.2.2)
(2.2.2.2)
και
![]() (2.2.2.3)
(2.2.2.3)
είναι συστήματα με μνήμη. Το σύστημα που περιγράφεται από τη σχέση (2.2.2.2) λέμε ότι απαιτεί πεπερασμένη μνήμη. Αντίθετα το σύστημα που περιγράφεται από τη σχέση (2.2.2.3) λέμε ότι απαιτεί απεριόριστη μνήμη.
2.2.3. Αμεταβλητότητα κατά τη μετατόπιση
Αμετάβλητο κατά τη μετατόπιση σύστημα (ΑΚΜ, SI: Shift invariant) λέγεται ένα σύστημα του οποίου η έξοδος εξαρτάται μόνο από το σήμα εισόδου και όχι από την χρονική στιγμή που αυτό εισήλθε στο σύστημα. Δηλαδή, αν η είσοδος x(n) καθυστερήσει κατά n0, τότε η έξοδος θα είναι η y(n) καθυστερημένη κατά n0. Μαθηματικά αυτό εκφράζεται ως ακολούθως. Έστω ότι το σύστημα δίνεται από τη σχέση
![]() (2.2.3.1)
(2.2.3.1)
η ολισθημένη είσοδος είναι
![]() (2.2.3.2)
(2.2.3.2)
και η αντίστοιχη έξοδος
![]() (2.2.3.3)
(2.2.3.3)
Το σύστημα Τ[.] είναι χρονικά αμετάβλητο κατά τη μετατόπιση αν
![]() (2.2.3.4)
(2.2.3.4)
Δηλαδή το σύστημα Τ[.] είναι χρονικά αμετάβλητο κατά τη μετατόπιση αν ισχύει η σχέση:
![]() (2.2.3.5)
(2.2.3.5)
Η προηγούμενη σχέση (2.2.3.5) ίσως δημιουργεί στο αναγνώστη την αίσθηση ότι πρέπει να αληθεύει πάντοτε αφού προκύπτει από την (2.2.3.3), αν θέσει όπου n την ποσότητα n-n0. Αυτό θα ήταν αληθές αν ο τελεστής Τ περιέγραφε μία συνάρτηση με μοναδική ανεξάρτητη μεταβλητή την x(n). Αυτό όμως δεν συμβαίνει στη γενική περίπτωση. Ας δούμε παραδείγματα χρονικά αμετάβλητων ή μεταβαλλόμενων κατά τη μετατόπιση συστημάτων.
Παράδειγμα
(Π.2.2.3.1)
Έστω το σύστημα που δίνεται από τη σχέση
![]() (2.2.3.6)
(2.2.3.6)
και περιγράφει ένα ενισχυτή πλάτους με κέρδος Κ που μένει σταθερό κατά τη διάρκεια λειτουργίας του.
Για την μετατοπισμένη είσοδο
![]() (2.2.3.7)
(2.2.3.7)
η αντίστοιχη έξοδος είναι
![]() (2.2.3.8)
(2.2.3.8)
Η y[n] μετατοπισμένη κατά n0 δίνεται από τη σχέση
![]() (2.2.3.9)
(2.2.3.9)
Από
τις (2.2.3.8) και (2.2.3.9) προκύπτει
ότι ![]() άρα το σύστημα είναι
χρονικά αμετάβλητο.
άρα το σύστημα είναι
χρονικά αμετάβλητο.
Παράδειγμα
(Π.2.2.3.2)
Έστω ότι στον ενισχυτή του προηγούμενου παραδείγματος το
κέρδος Κ μεταβάλλεται λόγω
δυσλειτουργίας (υπερθέρμανση) σύμφωνα με τη σχέση ![]() . Το σύστημα θα δίνεται από τη σχέση
. Το σύστημα θα δίνεται από τη σχέση
![]() (2.2.3.10)
(2.2.3.10)
Για την μετατοπισμένη είσοδο
![]() (2.2.3.11)
(2.2.3.11)
η αντίστοιχη έξοδος είναι
![]() (2.2.3.12)
(2.2.3.12)
Η y[n] μετατοπισμένη κατά n0 δίνεται από τη σχέση
![]() (2.2.3.13)
(2.2.3.13)
Από τις (2.2.3.12) και (2.2.3.13) προκύπτει ότι ![]() άρα το σύστημα είναι
χρονικά μεταβαλλόμενο.
άρα το σύστημα είναι
χρονικά μεταβαλλόμενο.
Παράδειγμα
(Π.2.2.3.3)
Έστω το σύστημα που δίνεται από τη σχέση
![]() (2.2.3.14)
(2.2.3.14)
Για την μετατοπισμένη είσοδο
![]() (2.2.3.15)
(2.2.3.15)
η αντίστοιχη έξοδος είναι
![]() (2.2.3.16)
(2.2.3.16)
Η y[n] μετατοπισμένη κατά n0 δίνεται από τη σχέση
![]() (2.2.3.17)
(2.2.3.17)
Από τις (2.2.3.16) και (2.2.3.17) προκύπτει ότι ![]() άρα το σύστημα είναι
χρονικά μεταβαλλόμενο.
άρα το σύστημα είναι
χρονικά μεταβαλλόμενο.
Ένα σύστημα λέγεται γραμμικό αν για αυτό ισχύουν οι ιδιότητες της ομογένειας και της επαλληλίας. Η αρχή της ομογένειας ισχύει για ένα διακριτό σύστημα όταν ισχύει η ακόλουθη σχέση
![]() (2.2.4.1)
(2.2.4.1)
όπου c είναι γενικά μιγαδική σταθερά
Η αρχή της επαλληλίας ισχύει για ένα σύστημα όταν ισχύει η σχέση
![]() (2.2.4.2)
(2.2.4.2)
Η γραμμικότητα ενός συστήματος μπορεί να περιγραφεί με μία μαθηματική σχέση ως ακολούθως
![]() (2.2.4.3)
(2.2.4.3)
Παράδειγμα (Π.2.2.4.1)
Έστω το σύστημα που δίνεται από τη σχέση
![]() (2.2.4.4)
(2.2.4.4)
![]() (2.2.4.5)
(2.2.4.5)
![]() (2.2.4.6)
(2.2.4.6)
Από τις (2.2.4.5) και (2.2.4.6) έπεται ότι το σύστημα έχει την ιδιότητα της ομογένειας.
![]() (2.2.4.7)
(2.2.4.7)
![]() =
=![]() (2.2.4.8)
(2.2.4.8)
Από τις (2.2.4.7) και (2.2.4.8) έπεται ότι το σύστημα έχει την ιδιότητα της επαλληλίας.
Δεδομένου ότι ισχύουν η ομογένεια και η επαλληλία το σύστημα είναι γραμμικό.
Παράδειγμα (Π.2.2.4.2)
Έστω το σύστημα που δίνεται από τη σχέση
![]() (2.2.4.9)
(2.2.4.9)
![]() (2.2.4.10)
(2.2.4.10)
![]() (2.2.4.11)
(2.2.4.11)
Από τις (2.2.4.10) και (2.2.4.11) έπεται ότι το σύστημα δεν έχει την ιδιότητα της ομογένειας.
![]() (2.2.4.12)
(2.2.4.12)
![]() (2.2.4.13)
(2.2.4.13)
Από τις (2.2.4.12) και (2.2.4.13) έπεται ότι το σύστημα δεν έχει την ιδιότητα της επαλληλίας. Δεδομένου ότι δεν ισχύουν η ομογένεια και η επαλληλία το σύστημα είναι δεν γραμμικό.
Εύκολα μπορεί να δειχθεί ότι
ένα σύστημα της μορφής
![]() (2.2.4.13)
(2.2.4.13)
όπου αk σταθερός όρος είναι γραμμικό και αμετάβλητο κατά την
μετατόπιση. Για παράδειγμα το σύστημα ![]() είναι LTI. Γραμμικό
και αμετάβλητο κατά την μετατόπιση είναι επίσης ένα σύστημα που περιγράφεται
από μια εξίσωση διαφορών της μορφής
είναι LTI. Γραμμικό
και αμετάβλητο κατά την μετατόπιση είναι επίσης ένα σύστημα που περιγράφεται
από μια εξίσωση διαφορών της μορφής
![]() (2.2.4.14)
(2.2.4.14)
Για παράδειγμα το σύστημα που
ικανοποιεί την σχέση ![]() είναι LTI. Εάν στο αριστερό μέρος της 2.2.4.14 κρατήσουμε μόνο
τον όρο y(n) η ακόλουθη σχέση περιγράφει ένα σύστημα LTI
είναι LTI. Εάν στο αριστερό μέρος της 2.2.4.14 κρατήσουμε μόνο
τον όρο y(n) η ακόλουθη σχέση περιγράφει ένα σύστημα LTI
![]() (2.2.4.15)
(2.2.4.15)
Το σύστημα ![]() είναι LTI.
είναι LTI.
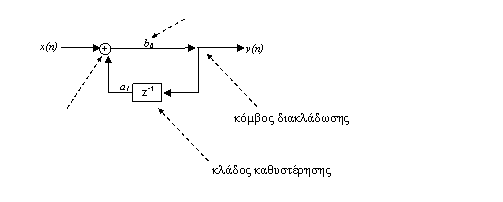
Οι σχέσεις 2.2.4.14 και 2.2..4.15 αποτελούν ένα αναδρομικό τρόπο
περιγραφής των συστημάτων.
Ένα
σύστημα λέγεται αιτιατό αν η τιμή της
εξόδου y(n) εξαρτάται από την τιμή x(n) του σήματος εισόδου και ενδεχομένως προηγούμενές της τιμές x(n-k), k φυσικός αριθμός. Διαφορετικά το
σύστημα λέγεται μη αιτιατό ή αντιαιτιατό. Για παράδειγμα το σύστημα ![]() είναι αιτιατό. Αντίθετα
το σύστημα
είναι αιτιατό. Αντίθετα
το σύστημα ![]() είναι μη αιτιατό. Τα
αιτιατά συστήματα καλούνται μη προβλέψιμα.
Όταν η μεταβλητή n αφορά τον
πραγματικό χρόνο (real time)
το σύστημα είναι μόνο αιτιατό αφού οι τιμές της εισόδου μετά τη τρέχουσα χρονική
στιγμή είναι άγνωστες. Εάν όμως η μεταβλητή n αφορά
τον χώρο ( θέσεις μνήμης, αύξοντες αριθμούς κ.λ.π.) είναι δυνατό το σύστημα να
είναι αιτιατό ή αντιαιτιατό. Ένα σύστημα επεξεργασίας ηχοσήματος σε πραγματικό
χρόνο είναι μόνο αιτιατό. Ένα σύστημα που αποθηκεύει τις τιμές ενός ηχοσήματος
και ακολούθως τις επεξεργάζεται μπορεί να είναι αιτιατό ή μη.
είναι μη αιτιατό. Τα
αιτιατά συστήματα καλούνται μη προβλέψιμα.
Όταν η μεταβλητή n αφορά τον
πραγματικό χρόνο (real time)
το σύστημα είναι μόνο αιτιατό αφού οι τιμές της εισόδου μετά τη τρέχουσα χρονική
στιγμή είναι άγνωστες. Εάν όμως η μεταβλητή n αφορά
τον χώρο ( θέσεις μνήμης, αύξοντες αριθμούς κ.λ.π.) είναι δυνατό το σύστημα να
είναι αιτιατό ή αντιαιτιατό. Ένα σύστημα επεξεργασίας ηχοσήματος σε πραγματικό
χρόνο είναι μόνο αιτιατό. Ένα σύστημα που αποθηκεύει τις τιμές ενός ηχοσήματος
και ακολούθως τις επεξεργάζεται μπορεί να είναι αιτιατό ή μη.
2.2.6. Ευστάθεια φραγμένης εισόδου-φραγμένης εξόδου
Ένα σύστημα λέγεται ότι είναι ευσταθές υπό την έννοια της φραγμένης εισόδου-φραγμένης εξόδου, αν
για οποιαδήποτε απολύτως φραγμένο σήμα εισόδου το σήμα εξόδου είναι και αυτό
απολύτως φραγμένο. Δηλαδή για οποιοδήποτε x(n)
![]() (2.2.6.1)
(2.2.6.1)
το σύστημα Τ[.] είναι ευσταθές φραγμένης
εισόδου-φραγμένης εξόδου.
Ένα σύστημα λέγεται αντιστρέψιμο αν μπορεί να προσδιοριστεί
μοναδικά το σήμα εισόδου από το σήμα εξόδου. Για να συμβαίνει αυτό θα πρέπει να
ισχύει η συνθήκη
![]() (2.2.7.1)
(2.2.7.1)
2.2.8. Απόκριση συστήματος σε
κρουστική διέγερση, το συνελικτικό άθροισμα
Την έξοδο ενός συστήματος όταν είσοδος του είναι η διακριτή κρουστική ώση αποκαλούμε απόκριση σε κρουστική διέγερση και την συμβολίζουμε ως h(n)
![]() (2.2.8.1) Έστω το γραμμικό ανεξάρτητο κατά την μετατόπιση
(Linear Sift Invariant:
LSI ή
αλλιώς Linear Time Invariant:
LTI) σύστημα T. Σύμφωνα με τη σχέση
(2.1.7.1) η έξοδος του συστήματος θα είναι
(2.2.8.1) Έστω το γραμμικό ανεξάρτητο κατά την μετατόπιση
(Linear Sift Invariant:
LSI ή
αλλιώς Linear Time Invariant:
LTI) σύστημα T. Σύμφωνα με τη σχέση
(2.1.7.1) η έξοδος του συστήματος θα είναι
![]() (2.2.8.2)
(2.2.8.2)
Επειδή το σύστημα είναι γραμμικό ισχύει η αρχή της επαλληλίας και της ομογένειας και ως εκ τούτου
![]() (2.2.8.3)
(2.2.8.3)
![]() (2.2.8.4)
(2.2.8.4)
![]() (2.2.8.5)
(2.2.8.5)
Αν το σύστημα είναι ανεξάρτητο κατά την μετατόπιση τότε
![]() (2.2.8.6)
(2.2.8.6)
Από τις σχέσεις 2.2.8.5 και 2.2.8.6 συνεπάγεται ότι η έξοδος ενός γραμμικού ανεξάρτητο κατά τη μετατόπιση συστήματος σε οποιαδήποτε είσοδο x(n), δίνεται από τη σχέση
![]() (2.2.8.7)
(2.2.8.7)
Η σχέση 2.2.8.7 λέγεται και συνελικτικό άθροισμα των ακολουθιών x(n), και h(n)
Γενικά, για δύο ακολουθίες x(n), και y(n) το συνελικτικό άθροισμα τους συμβολίζεται ![]() ή
ή ![]() και δίνεται από τη σχέση
και δίνεται από τη σχέση
![]() =
=![]() =
=![]() (2.2.8.8)
(2.2.8.8)
Συχνά χρησιμοποιείται η ονομασία συνέλιξη των διακριτών σημάτων εννοώντας το συνελικτικό άθροισμα. Από τη σχέση 2.2.8.7 συμπεραίνουμε ότι αν γνωρίζουμε την απόκριση σε κρουστική διέγερση ενός συστήματος LTI, μπορούμε να υπολογίσουμε την έξοδό του σε οποιαδήποτε είσοδο από τη σχέση
y(n)=x(n)* h(n) (2.8.8.9)
Για το λόγο αυτό λέμε ότι η απόκριση σε κρουστική διέγερση ενός συστήματος LTI το προσδιορίζει πλήρως. Από την απόκριση σε κρουστική διέγερση ενός LTI συστήματος ελέγχεται η αιτιότητα και η ευστάθειά του. Συγκεκριμένα αφού σε ένα αιτιατό σύστημα η έξοδος δεν εξαρτάται από τιμές τις εισόδου που ακολουθούν την τιμή x(n) τότε η απόκρισή του σε κρουστική διέγερση είναι ένα σήμα δεξιάς πλευράς διότι δεν εξαρτάται από τιμές δ(n+n0), n0>0. Ένα σύστημα LTI με απόκριση σε κρουστική διέγερση h(n) είναι ευσταθές ΒΙΒΟ αν ισχύει η συνθήκη
![]() (2.8.8.10)
(2.8.8.10)
Απόδειξη
Για
κάθε φραγμένο σήμα εισόδου x(n) ισχύει
ότι![]() . Αν h(n) η
απόκριση σε κρουστική διέγερση ενός LTI συστήματος για την έξοδό του y(n) θα ισχύει ότι
. Αν h(n) η
απόκριση σε κρουστική διέγερση ενός LTI συστήματος για την έξοδό του y(n) θα ισχύει ότι
 (2.8.8.11)
(2.8.8.11)
Άρα για να είναι BIBO ευσταθές το σύστημα πρέπει και αρκεί να ισχύει η (2.8.8.10).
2.2.9.Ιδιότητες της συνέλιξης διακριτών σημάτων
Η συνέλιξη δύο ακολουθιών είναι μια πράξη (τελεστής) μεταξύ δυο ακολουθιών. Είναι γραμμικός τελεστής και έχει την αντιμεταθετική, προσαιτεριστική και επιμεριστική ως την πρόσθεση ιδιότητα.
Η αντιμεταθετική ιδιότητα
![]() (2.2.9.1)
(2.2.9.1)
Απόδειξη
![]() , θέτωντας m=n-k (2.2.9.2)
, θέτωντας m=n-k (2.2.9.2)
![]() (2.2.9.3)
(2.2.9.3)
Η προσεταιριστική ιδιότητα
![]() (2.2.9.4)
(2.2.9.4)
Η απόδειξη γίνεται με κατάλληλη αντικατάσταση των δεικτών και αφήνεται ως άσκηση στον αναγνώστη. Αν δύο συστήματα LTI με αποκρίσεις κρουστικής διέγερσης h1(n) και h2(n) είναι συνδεδεμένα σε σειρά, η προσεταιριστική ιδιότητα έχει σαν αποτέλεσμα τα δύο συστήματα να ισοδυναμούν με ένα σύστημα με κρουστική απόκριση h(n)= h1(n)* h2(n)
Η επιμεριστική ιδιότητα ως προς την πρόσθεση
![]() (2.2.9.5)
(2.2.9.5)
Η απόδειξη αφήνεται ως άσκηση στον αναγνώστη. Αν δύο συστήματα LTI με αποκρίσεις κρουστικής διέγερσης h1(n) και h2(n) είναι συνδεδεμένα παράλληλα, η επιμεριστική ιδιότητα έχει σαν αποτέλεσμα τα δύο συστήματα να ισοδυναμούν με ένα σύστημα με κρουστική απόκριση h(n)= h1(n)+ h2(n)
2.2.10. Τρόποι υπολογισμού της συνέλιξης διακριτών σημάτων
Ο υπολογισμός της συνέλιξης δύο ακολουθιών που ορίζονται αλγεβρικά μπορεί να γίνει με χρήση ταυτοτήτων που αφορούν αθροίσματα όρων και όρια σύγκλισης ακολουθιών όπως στα ακόλουθα παραδείγματα
Να υπολογισθεί η συνέλιξη u(n)* u(n-n0)
![]() (2.2.10.1)
(2.2.10.1)
![]()
Να
υπολογισθεί η συνέλιξη ![]() ,
, ![]()
 (2.2.10.2)
(2.2.10.2)
Αν x(n) και y(n) σήματα με πεπερασμένα μήκη Νx και Νy, στα διαστήματα [Lx, Rx] και [Lx, Rx] αντίστοιχα η συνέλιξη τους θα είναι
![]() με
με
![]() (2.2.10.3)
(2.2.10.3)
και
![]() (2.2.10.4)
(2.2.10.4)
![]() (2.2.10.5)
(2.2.10.5)
Από τις σχέσεις (2.2.10.3) και (2.2.10.4) προκύπτει με πρόσθεση κατά μέλη ότι
![]() (2.2.10.6)
(2.2.10.6)
και
![]() (2.2.10.7)
(2.2.10.7)
Συνεπώς το αποτέλεσμα της συνέλιξης των δύο σημάτων θα είναι ένα σήμα με πεπερασμένο μήκος Ν=Νx+Νy-1 στο διάστημα [Lx+ Ly, Rx+ Ry] και τιμές
.
![]() (2.2.10.8)
(2.2.10.8)
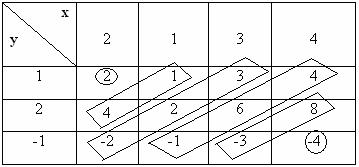
Για την εκτέλεση της συνέλιξης σημάτων πεπερασμένου μήκους που περιγράφονται από τις αριθμητικές τιμές τους, οργανώνουμε τους υπολογισμούς, γράφοντας αρχικά τα σήματα όπως απαιτεί ο ορισμός του συνελικτικού αθροίσματος για κάθε τιμή του n στο διάστημα [Lx+ Ly, Rx+ Ry] και ακολούθως εκτελούμε τις πράξεις. Για παράδειγμα αν x=[2 1 3 4] με Lx=0 και y=[1 2 -1] με Ly=0 οι τιμές των μεταβλητών n,k και των σημάτων x(n) και y(n-k) φαίνονται στoν Πιν.2.2.10.1, του οποίου οι γραμμοσκιασμένες περιοχές περιέχουν τις τιμές εκτέλεσης πράξεων για τον υπολογισμό της συνέλιξης. Η σκιασμένη περιοχή περιέχει τα γινόμενα με παράγοντες όλους τους συνδυασμούς ανά δύο, των τιμών των δύο σημάτων. Από αυτές τις τιμές η διαδικασία της ολίσθησης καθορίζει ποια γινόμενα θα χρησιμοποιηθούν στο υπολογισμό του συνελικτικού αθροίσματος για κάθε τιμή της ακέραιας μεταβλητής n Η διαδικασία μπορεί να συμπτυχθεί όπως φαίνεται στον Πιν.2.2.10.2.
|
|
k |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
x(k) |
0 |
0 |
0 |
0 |
2 |
1 |
3 |
4 |
0 |
0 |
|
|
|
N |
y(n-k) |
|
|
|
|
|
|
|
|
|
|
|
{x*y}(n) |
|
-1 |
y(-1-k) |
0 |
-1 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0∙0 |
0 |
|
0 |
y(-k) |
0 |
0 |
-1 |
2 |
1 |
0 |
0 |
0 |
0 |
0 |
2∙1 |
2 |
|
1 |
y(1-k) |
0 |
0 |
0 |
-1 |
2 |
1 |
0 |
0 |
0 |
0 |
2∙2+1∙1 |
5 |
|
2 |
y(2-k) |
0 |
0 |
0 |
0 |
-1 |
2 |
1 |
0 |
0 |
0 |
2∙(-1)+2∙1+3∙1 |
3 |
|
3 |
y(3-k) |
0 |
0 |
0 |
0 |
0 |
-1 |
2 |
1 |
0 |
0 |
1∙(-1)+3∙2+4∙1 |
9 |
|
4 |
y(4-k) |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
2 |
1 |
0 |
3∙(-1)+4∙2 |
5 |
|
5 |
y(5-k) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
2 |
1 |
4∙(-1) |
-4 |
|
6 |
y(6-k) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
2 |
0∙0 |
0 |
|
7 |
y(7-k) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0∙0 |
0 |
|
Πίνακας 2.2.10.1 |
|||||||||||||
|
|
|
Πίνακας 2.2.10.2 |
ΚΕΦΑΛΑΙΟ 3
Περί μετασχηματισμών σημάτων διακριτού χρόνου.
Υπάρχει ένα πλήθος μετασχηματισμών που χρησιμοποιούνται στην ανάλυση των σημάτων και των συστημάτων. Οι πιο βασικοί είναι, ο μετασχηματισμός Fourier και ο μετασχηματισμός Ζ. Άλλοι μετασχηματισμοί είναι αυτοί του συνημιτόνου του ημιτόνου, ο Sort Τime Fourier Transform και τα κυμματίδια (wavelets). Οι μετασχηματισμοί Fourier, ημιτόνου και συνημιτόνου, είναι μετασχηματισμοί των διακριτών σημάτων σε ορθοκανονικές και ορθομοναδιαίες βάσεις Υπάρχει πλούσια βιβλιογραφία για τον ορισμό των μετασχηματισμών αυτών και την αυστηρή μαθηματική τους διερεύνηση. Εδώ θα εστιάσουμε στην ερμηνεία τους ώστε να βοηθηθεί ο αναγνώστης να αντιληφθεί γεωμετρικά και παραστατικά την βασική ιδέα από τις συνήθεις μαθηματικές εκφράσεις τους. Αυτό θα βοηθήσει σημαντικά στην δυνατότητά του να κατανοήσει την χρήση των μετασχηματισμών αυτών σε διάφορα πεδία (σχεδιασμός φίλτρων, συμπίεση) καθώς και να προχωρήσει στην κατανόηση της φύσης πιο σύνθετων μετασχηματισμών όπως τα κυμματίδια
3.2 Ερμηνεία μετασχηματισμών με διανυσματική ανάλυση.
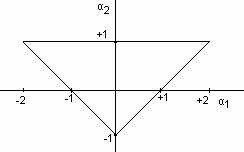
Ας υποθέσουμε λοιπόν για λόγους απλότητας και για να έχουμε τη δυνατότητα γεωμετρικής αναπαράστασης, το σήμα με πεπερασμένο μήκος N=2 (Σχ.3.2.1) και πραγματικές τιμές x[0], x[1].
Σχήμα 1.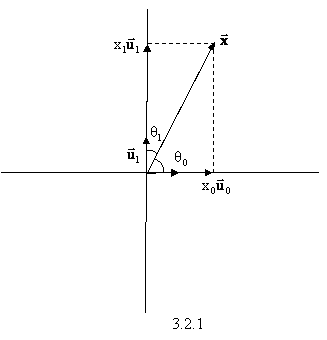
Το άνυσμα ![]() με συντεταγμένες (x0, x1)
με x0=x[0], x1=x[1], γράφεται με
την άλγεβρα των ανυσμάτων σύμφωνα με τον κανόνα του παραλληλογράμμου ως
με συντεταγμένες (x0, x1)
με x0=x[0], x1=x[1], γράφεται με
την άλγεβρα των ανυσμάτων σύμφωνα με τον κανόνα του παραλληλογράμμου ως
(3.2.1) ![]()
όπου
![]() και
και ![]() ανύσματα κάθετα μεταξύ τους με μήκος τη μονάδα και
συντεταγμένες (1,0) και (0,1) αντίστοιχα στο ορθογώνιο σύστημα αξόνων που
ορίζουν. Επειδή τα
ανύσματα κάθετα μεταξύ τους με μήκος τη μονάδα και
συντεταγμένες (1,0) και (0,1) αντίστοιχα στο ορθογώνιο σύστημα αξόνων που
ορίζουν. Επειδή τα ![]() και
και ![]() είναι κάθετα μεταξύ τους ο κανόνας του παραλληλογράμμου έχει
ως αποτέλεσμα οι τιμές x0 και x1 να
είναι οι προβολές του
είναι κάθετα μεταξύ τους ο κανόνας του παραλληλογράμμου έχει
ως αποτέλεσμα οι τιμές x0 και x1 να
είναι οι προβολές του ![]() σ’ αυτά. Ακόμη, επειδή
τα
σ’ αυτά. Ακόμη, επειδή
τα ![]() και
και ![]() έχουν μέτρο τη μονάδα,
οι συντεταγμένες x0,
x1 δίνονται
από τις σχέσεις:
έχουν μέτρο τη μονάδα,
οι συντεταγμένες x0,
x1 δίνονται
από τις σχέσεις:
(3.2.2) x0=|![]() |cos(θ0)
και x1= |
|cos(θ0)
και x1= |![]() |cos(θ1)
|cos(θ1)
Υπενθυμίζεται
ότι για το εσωτερικό γινόμενο των ανυσμάτων ![]() (x0,x1) και
(x0,x1) και ![]() (y0,y1) ισχύει
(y0,y1) ισχύει
(3.2.3)![]() .
.
Επειδή τα ![]() και
και ![]() έχουν μέτρο τη μονάδα
(μοναδιαία ανύσματα) ισχύει:
έχουν μέτρο τη μονάδα
(μοναδιαία ανύσματα) ισχύει:
(3.2.4) ![]() και
και ![]()
Ζεύγη κάθετων διανυσμάτων με μήκος μονάδα υπάρχουν απείρου πλήθους, για παράδειγμα τα:
![]()
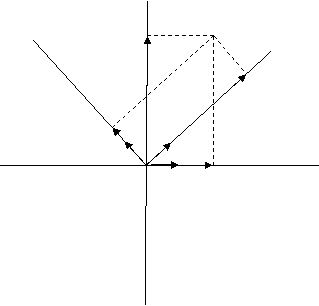
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() και
και
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() και
και
![]() , (0,-1) με (1,0).
, (0,-1) με (1,0).

Έστω ![]() (g00,
g01) και
(g00,
g01) και ![]() (g10,
g11)
διανύσματα κάθετα μεταξύ τους με μήκος μονάδα έκαστο όπως δείχνει το Σχ.3.3.2.
Το άνυσμα
(g10,
g11)
διανύσματα κάθετα μεταξύ τους με μήκος μονάδα έκαστο όπως δείχνει το Σχ.3.3.2.
Το άνυσμα ![]() γράφεται σαν άθροισμα
γράφεται σαν άθροισμα
(3.2.5)![]()
όπου
c0 και c1 οι προβολές του
![]() στα
στα ![]() και
και ![]() . Επειδή τα
. Επειδή τα ![]() και
και ![]() είναι κάθετα μεταξύ τους ο κανόνας του παραλληλογράμμου
έχει ως αποτέλεσμα οι τιμές c0, c1 να
είναι οι προβολές του
είναι κάθετα μεταξύ τους ο κανόνας του παραλληλογράμμου
έχει ως αποτέλεσμα οι τιμές c0, c1 να
είναι οι προβολές του ![]() σ’ αυτά. Ακόμη, επειδή
τα
σ’ αυτά. Ακόμη, επειδή
τα ![]() και
και ![]() έχουν μέτρο τη
μονάδα, οι συντεταγμένες c0,
c1 δίνονται
από τις σχέσεις:
έχουν μέτρο τη
μονάδα, οι συντεταγμένες c0,
c1 δίνονται
από τις σχέσεις:
(3.2.6)![]() και
και ![]()
Αντικαθιστώντας
το ![]() από την (1.1) στις (1.6)
από την (1.1) στις (1.6)
(3.2.7)![]()
και αν χρησιμοποιήσουμε την γραφή x0=x[0] και g00=g0[0], g01=g0[1] που χρησιμοποιείται στα σήματα διακριτού χρόνου.
(3.2.8)![]()
Όμοια έχουμε
(3.2.9)![]()
Για να υπολογίσουμε τα x[0], x[1] από τα c0
, c1
αντικαθιστούμε από την σχέση (3.2.5) το ![]() στις (1.4)
στις (1.4) ![]() και
και ![]() οπότε
οπότε
(3.2.10)![]()
και αν χρησιμοποιήσουμε την γραφή x0=x[0] και g00=g0[0], g10=g1[0] που χρησιμοποιείται στα σήματα διακριτού χρόνου
(3.2.11)![]()
Όμοια έχουμε
(3.2.12) ![]()
3.3 Ερμηνεία
μετασχηματισμών με γραμμική άλγεβρα
Η περιγραφή του σήματος με διανυσματική αναπαράσταση, γραφή και υπολογισμούς, μπορεί να γίνει με την χρήση της γραμμικής άλγεβρας που αποτελεί εξαιρετικό εργαλείο για τα σήματα διακριτού χρόνου, χωρίς των περιορισμό του φυσικού χώρου των ανυσμάτων
(3.3.1) ![]() ,.
,.![]() ,
,![]()
Τα διανύσματα u0, u1 είναι μοναδιαία και κάθετα μεταξύ τους (ορθοκανονικά) και αποτελούν μία ορθοκανονική βάση. Ισχύουν προφανώς οι σχέσεις:
(3.3.2) ![]() και
και ![]()
(3.3.3) ![]() και
και ![]()
Παρατηρείστε τον συσχετισμό των σχέσεων (1.4), (2.3).
(3.3.4) ![]() =
=![]()
Παρατηρείστε τον συσχετισμό των σχέσεων (3.2.1), (3.3.4).
Τα ![]() και
και ![]() έχουν τιμές των δ[n] και δ[n-1]
αντίστοιχα και ως γνωστόν ισχύει η σχέση
έχουν τιμές των δ[n] και δ[n-1]
αντίστοιχα και ως γνωστόν ισχύει η σχέση
(3.3.5)![]()
παρατηρούμε την ομοιότητα των σχέσεων (3.3.5) , (3.3.4) και (3.2.1).
Αν 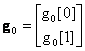 ,
, ![]() =
=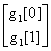 ζεύγος ορθοκανονικών διανυσμάτων και
ζεύγος ορθοκανονικών διανυσμάτων και ![]() , θα ισχύουν οι σχέσεις:
, θα ισχύουν οι σχέσεις:
(3.3.6) ![]() και
και ![]()
οι προβολές του x σ’αυτά θα δίνονται ως εσωτερικά γινόμενα από τις σχέσεις:
(3.3.7)![]() =
= ![]()
(3.3.8) ![]() =
=![]()
Παρατηρείστε την ομοιότητα των σχέσεων (3.3.7) και (3.3.8) με τις (3.2.6). και ότι καταλήγουν στις (3.2.8) και (3.2,9). Γενικά αν k=0..N-1 και n = 0..N-1, θα ισχύει ότι
(3.3.9) ![]()
Με βάση τα παραπάνω αν 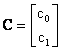 , ισχύει ότι
, ισχύει ότι
(3.3.10) ![]()
Το ζητούμενο τώρα είναι να υπολογισθεί ο x αν είναι γνωστοί οι πίνακες G και C. Αν υπάρχει ο πίνακας G-1 (αντίστροφος του G) τότε
(3.3.11) ![]()
Επειδή η βάση είναι ορθοκανονική ισχύουν οι (3.3.2) αρα
(3.3.12) 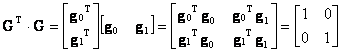 =ΙÞ
=ΙÞ
(3.3.13) G=(GT)-1Þ
(3.3.14) ![]() Þ
Þ
(3.3.15)![]()
(3.3.16) ![]() και
και
(3.3.17) ![]()
Οι σχέσεις (3.3.16) και (3.3.17) είναι ίδιες με τις (3.2.11) και (3.2.12). Στις πρώτες οδηγηθήκαμε από την (3.3.13) ενώ στις δεύτερες από τον κανόνα του παραλληλογράμμου, και στις δύο περιπτώσεις όμως βασισθήκαμε στην ορθοκανονικότητα των διανυσμάτων της βάσης.
Γενικά αν n=0..N-1 και k = 0..N-1, θα ισχύει
(3.3.18) ![]() δηλαδή ένα
ανάπτυγμα του x[n] σε σειρά των gk[n]
δηλαδή ένα
ανάπτυγμα του x[n] σε σειρά των gk[n]
Τα παραπάνω ισχύουν για οποιεσδήποτε τιμές του Ν και η σχέση (3.3.9)
|
|
υπολογίζει τις προβολές (συντελεστές αναπτύγματος σειράς) του διακριτού σήματος (ακολουθίας) στο σύστημα συντεταγμένων που ορίζει ο πίνακας G, ενώ η σχέση (3.3.18)
|
|
δίνει τις τιμές x[n] του σήματος.
Για παράδειγμα για Ν=3 τα ανύσματα
![]() ,
, ![]() ,
, ![]()
αποτελούν μία
ορθοκανονική βάση και το σήμα x=[1, 3, 2] προβάλλεται σ’αυτά με προβολές που δίνουν οι
συντελεστές ![]() ,
, ![]() ,
, ![]() . Για n=0,1,2
. Για n=0,1,2
x[n]= ![]()
![]()
![]()
Τα προηγούμενα ορθοκανονικά διανύσματα προήλθαν θέτοντας Ν=3 στις σχέσεις
(3.3.19)![]() για k=1..N-1 και n=0,..,Ν-1
για k=1..N-1 και n=0,..,Ν-1
οπότε προέκυψαν οι τιμές των g0, g1, g2 από τις σχέσεις
(3.3.20)![]()
![]()
3.4 Ο διακριτός μετασχηματισμός
συνημιτόνου (DCT: Discrete
Cosine Transform)
H σχέση (3.3.19) ![]() για k=1..N-1 και n=0,..,Ν-1 είναι ένας πυρήνας (kernel) δημιουργίας
ορθοκανονικών διανυσμάτων για κάθε τιμή του Ν. Γενικά αν τα gk δίνονται
από την (2.19) οι συντελεστές ck για ένα διακριτό σήμα x[n] (δηλαδή οι προβολές του x στα gk) προκύπτουν με
αντικατάσταση των gk από την (3.3.19) στη
(3.3.9) από τη σχέση:
για k=1..N-1 και n=0,..,Ν-1 είναι ένας πυρήνας (kernel) δημιουργίας
ορθοκανονικών διανυσμάτων για κάθε τιμή του Ν. Γενικά αν τα gk δίνονται
από την (2.19) οι συντελεστές ck για ένα διακριτό σήμα x[n] (δηλαδή οι προβολές του x στα gk) προκύπτουν με
αντικατάσταση των gk από την (3.3.19) στη
(3.3.9) από τη σχέση:
(3.4.1) ![]() ,
, ![]() για k=1..N-1
για k=1..N-1
Η σχέση (3.4.1) αποτελεί τον μονοδιάστατο διακριτό μετασχηματισμό συνημιτόνου (1D-DCT: Discrete Cosine Transform). Οι τιμές x[n] (δηλαδή το x) προκύπτουν με αντικατάσταση των gk από τις (3.3.19) στη (3.3.18) σύμφωνα με τη σχέση
(3.4.2)![]()
Η σχέση (3.4.2) αποτελεί τον αντίστροφο διακριτό μετασχηματισμό του συνημιτόνου.
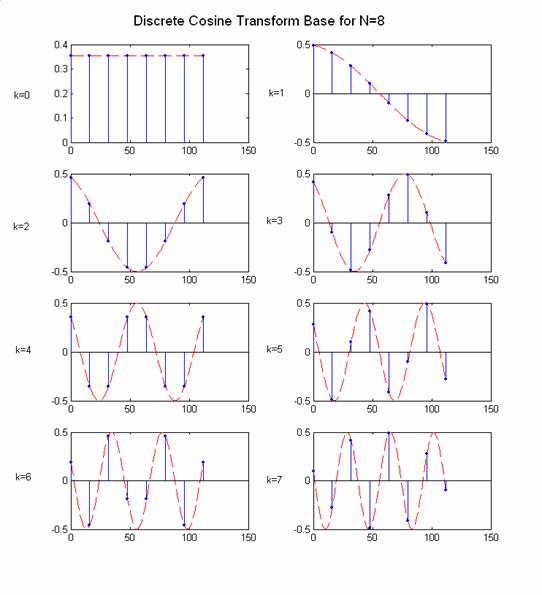
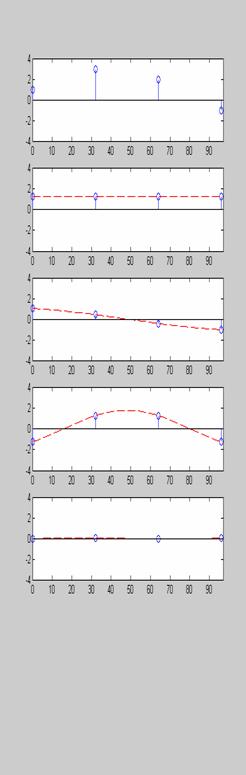
Στο Σχ.3.4.1 δείχνονται τα ανύσματα βάσης του DCT για Ν=8.
ΠΑΡΑΔΕΙΓΜΑΤΑ
1) Για παράδειγμα για Ν=3 τα ανύσματα
![]() ,
, ![]() ,
, ![]()
προήλθαν από τις σχέσεις
![]() για k=1..N-1 και n=0,..,Ν-1
για k=1..N-1 και n=0,..,Ν-1
αποτελούν μία
ορθοκανονική βάση και το σήμα x=[1, 3, 2]Τ προβάλλεται σ’ αυτά με προβολές που
δίνουν οι συντελεστές ![]() ,
, ![]() ,
, ![]() . Για n=0,1,2
. Για n=0,1,2
x[n]= ![]()
![]()
![]()
2) Για x=[1, 3, 2, -1]Τ η τιμή Ν=4 και για n=0,1,2,3 τα ανύσματα βάσης είναι:
|
|
Ή |
g0=[0.50, 0.50,
0.50, 0.50]T |
|
|
Ή |
g1=[0.65, 0.27, -0.27, -0.65]T |
|
|
Ή |
g2=[0.50,
-0.50, 0.50, -0.50]T |
|
|
Ή |
g3=[0.27,
-0.65. 0.65, -0.27]T |
Οι συντελεστές ck είναι τα στοιχεία του πίνακα
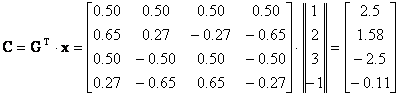
οι συντελεστές ck προκύπτουν όμοια και από τις (3.1.1) Το σήμα ανακτάται από τις σχέσεις (3.1.2) ή από τον πίνακα
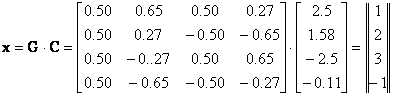
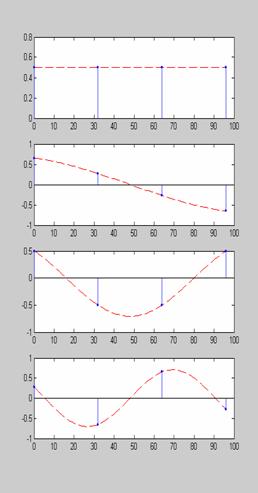
Στο Σχ.3.4.2 δείχνονται τα ανύσματα βάσης του DCT για Ν=4, οι συντελεστές ck του DCT του σήματος x=[1, 3, 2, -1] και η ανάλυση του στις τέσσερις συνιστώσες ckgk. Κάθε τιμή του x[n] είναι x[n]=2,5g0[n]+ 1,58g1[n]-2,5g2[n]-0,11g3[n] .
.
|
|
|
Σχήμα 3.4.1 |
|
|
x=[1,
3, 2, –1] g1[n] 2,5×g1[n] g2[n] 1,58×g2[n] g2[n] -2,5×g2[n] g3[n] -0,11×g3[n] |
|
|
Σχήμα 3.4.2. |
|
|
3.4.1 Ο δισδιάστατος (2Δ) διακριτός
μετασχηματισμός συνημιτόνου (2D-DCT: Discrete Cosine Transform)
![]() Για
διακριτά σήματα δύο διαστάσεων με μήκη Ν1, Ν2 τα ανύσματα
βάσης για n1=0,..,N1-1, n2=0,..,N2-1, k1=0,..,N1-1, k2=0,..,N2-1 είναι:
Για
διακριτά σήματα δύο διαστάσεων με μήκη Ν1, Ν2 τα ανύσματα
βάσης για n1=0,..,N1-1, n2=0,..,N2-1, k1=0,..,N1-1, k2=0,..,N2-1 είναι:
![]() (3.4.1.1)
(3.4.1.1) ![]()
|
|
Για ένα δισδιάστατο διακριτό σήμα x[n1,n2] με μήκη Ν1, Ν2, οι προβολές του στα παραπάνω ορθοκανονικά ανύσματα βάσης είναι:
(3.4.1.2)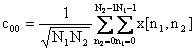
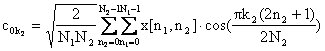
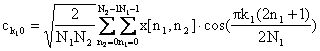
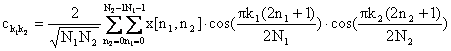
για k1,k2 ¹0.
Οι παραπάνω σχέσεις αποτελούν τον δισδιάστατο (2Δ) διακριτό μετασχηματισμό συνημιτόνου (2D-DCT: Discrete Cosine Transform). Το σήμα x[n1,n2] ανακτάται σύμφωνα με τη σχέση:
(3.4.1.3) ![]()
που είναι ο αντίστροφος δισδιάστατος (2Δ) διακριτός μετασχηματισμός συνημιτόνου.
Μετασχηματισμοί των οποίων η βάση ικανοποιεί την (3.4.1.1) λέγονται διαχωρίσιμοι και οι υπολογισμοί τους μπορούν να αναχθούν σε υπολογισμούς των μονοδιάστατων εκφράσεών τους.
3.5 Ερμηνεία και υπολογισμοί
μετασχηματισμών μιγαδικών σημάτων διακριτού χρόνου.
Ας εξετάσουμε τώρα αν τα παραπάνω μπορούν να εφαρμοσθούν και σε μιγαδικά
διακριτά σήματα πεπερασμένου μήκους. Η διανυσματική περιγραφή τέτοιων σημάτων
γίνεται με πίνακες στήλης που τα στοιχεία τους είναι μιγαδικοί αριθμοί. Οι
σχέσεις που καταλήξαμε στην περίπτωση των πραγματικών σημάτων πεπερασμένου
μήκους Ν (xÎRN) είναι αποτέλεσμα του
γεγονότος ότι αναλύσαμε το σήμα σε μία βάση ορθοκανονικών διανυσμάτων,
διανυσμάτων δηλαδή που έχουν μέτρο ίσο με την μονάδα και είναι μεταξύ τους
κάθετα. Προς τούτο χρησιμοποιήσαμε (σχέσεις (2.2)) την πράξη xΤy για x,yÎRN . Αν όμως
εκφράσουμε τον μιγάδα 1+j
που έχει μέτρο ![]() σε διανυσματική μορφή
σε διανυσματική μορφή ![]() , η πράξη
, η πράξη ![]() και όχι 2 όπως θα
έπρεπε. Επειδή για το μέτρο ενός μιγάδα z=a+bj ισχύει ότι
και όχι 2 όπως θα
έπρεπε. Επειδή για το μέτρο ενός μιγάδα z=a+bj ισχύει ότι ![]() , η πράξη
, η πράξη ![]() =a2+b2,
με
=a2+b2,
με ![]() δίνει το επιθυμητό
αποτέλεσμα. Το ίδιο ισχύει και με τον υπολογισμό της προβολής του διανύσματος
ενός μιγάδα στο διάνυσμα ενός άλλου. Εάν τελικά για ένα μιγαδικό διάνυσμα x με Ν μιγαδικές τιμές (
δίνει το επιθυμητό
αποτέλεσμα. Το ίδιο ισχύει και με τον υπολογισμό της προβολής του διανύσματος
ενός μιγάδα στο διάνυσμα ενός άλλου. Εάν τελικά για ένα μιγαδικό διάνυσμα x με Ν μιγαδικές τιμές (![]() CN) ορίσουμε ως τετράγωνο του μέτρου την
ποσότητα
CN) ορίσουμε ως τετράγωνο του μέτρου την
ποσότητα ![]() εξασφαλίζουμε ότι αυτή είναι πραγματικός αριθμός. Δύο
μιγαδικά διανύσματα (πίνακες στήλης) g0, g1λέγονται ορθομοναδιαία αν
εξασφαλίζουμε ότι αυτή είναι πραγματικός αριθμός. Δύο
μιγαδικά διανύσματα (πίνακες στήλης) g0, g1λέγονται ορθομοναδιαία αν
(3.5.1) ![]() και
και![]()
Στη γραμμική άλγεβρα ο συζυγής ενός μιγαδικού πίνακα Α, γράφεται ![]() και αποτελείται
από τα συζυγή στοιχεία του Α. Ο ανάστροφος του συζυγούς του Α,
δηλαδή ο
και αποτελείται
από τα συζυγή στοιχεία του Α. Ο ανάστροφος του συζυγούς του Α,
δηλαδή ο![]() , λέγεται αναστροφοσυζυγής του Α ή Α
Ερμιτιανός και γράφεται ΑΗ. Συνεπώς η (4.1) γράφεται
, λέγεται αναστροφοσυζυγής του Α ή Α
Ερμιτιανός και γράφεται ΑΗ. Συνεπώς η (4.1) γράφεται
(3.5.2) ![]() και
και ![]()
Αν
(3.5.3) G=[g0, g1, …, gN-1] πίνακας ορθομοναδιαίων διανυσμάτων τότε ο
(3.5.4) 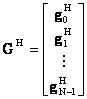 και ισχύει ότι
και ισχύει ότι
(3.5.5) GHG=I άρα
(3.5.6) GH=G-1
Ακριβώς όπως και στην περίπτωση των ορθοκανονικών βάσεων ένα μιγαδικό
διάνυσμα ![]() CN μπορεί να προβληθεί
σε ορθομοναδιαία μιγαδικά διανύσματα gk Î CN, k=0,..,N-1 με μιγαδικές εν γένει προβολές ck (ckÎ CN). Με βάση τους
παραπάνω όρισμούς και πράξεις όπως αυτές που ακολουθήσαμε στην περίπτωση των
πραγματικών διανυσμάτων ισχύουν οι σχέσεις:
CN μπορεί να προβληθεί
σε ορθομοναδιαία μιγαδικά διανύσματα gk Î CN, k=0,..,N-1 με μιγαδικές εν γένει προβολές ck (ckÎ CN). Με βάση τους
παραπάνω όρισμούς και πράξεις όπως αυτές που ακολουθήσαμε στην περίπτωση των
πραγματικών διανυσμάτων ισχύουν οι σχέσεις:
(3.5.7)![]()
(3.5.8) και x=G×C (λόγω της (3.5.6) )
και x=G×C (λόγω της (3.5.6) )
(3.5.9)![]()
(3.5.10) ![]() , δηλαδή ένα ανάπτυγμα του x[n] σε σειρά των gk[n]
, δηλαδή ένα ανάπτυγμα του x[n] σε σειρά των gk[n]
Ο ερμιτιανός ενός πίνακα πραγματικών αριθμών είναι ο ανάστροφος του, συνεπώς οι σχέσεις που καταλήξαμε για τα πραγματικά διανύσματα είναι ειδικές περιπτώσεις των σχέσεων που ισχύουν για τα μιγαδικά.
ΚΕΦΑΛΑΙΟ 4
Ο μετασχηματισμός Fourier
. Όπως προαναφέρθηκε ο μετασχηματισμός Fourier είναι θεμελιώδους σημασίας στην ανάλυση των σημάτων και των συστημάτων συνεχούς ή διακριτής ανεξάρτητης μεταβλητής. Μέσω αυτού περιοδικές συναρτήσεις και ακολουθίες αναλύονται σε αθροίσματα όρων που καθένας τους εκφράζει μία αρμονική ταλάντωση. Στο κεφάλαιο αυτό θα αναφερθούμε στο διακριτό μετασχηματισμό Fourier (Discrete Fourier Transform, DFT), την διακριτή σειρά Fourier (Discrete Fourier Seiries, DFS), τον μετασχηματισμό Fourier διακριτού χρόνου (Discrete Time Fourier Transform, DTFT) και τον αντίστροφο μετασχηματισμό Fourier. Οι ορισμοί, οι ιδιότητες, οι μεταξύ τους σχέσεις και σχέσεις του με τα συνελικτικά αθροίσματα αποτελούν προϋπόθεση για την κατανόηση της χρήσης του στην ανάλυση των σημάτων και των συστημάτων.
4.2 Ο διακριτός μετασχηματισμός Fourier-N σημείων.
Ένας πυρήνας παραγωγής ορθομοναδιαίων διανυσμάτων είναι ο τύπος
(4.2.1) ![]() =
=![]() όπου
όπου ![]()
Η βάση είναι ορθομοναδιαία διότι ισχύουν οι σχέσεις (3.5.1) όπως δείχνεται ακολούθως
(4.2.2) ![]()
(4.2.3) για k¹m
για k¹m
Από τις (3.5.9) και (3.5.10) προκύπτουν οι συντελεστές και το ανάπτυγμα
σε σειρά ενός πεπερασμένου μήκους Ν σήματος x
(4.2.4) ![]()
(4.2.5) ![]()
H σχέση (4.2.4) αποτελεί τον μοναδιαίο (unitary) διακριτό μετασχηματισμό Fourier (Discrete Time Fourier Transform ή DFT) N-σημείων και η (4.2.5) την αντίστοιχη σειρά.
Αν θέσουμε ![]() στις παραπάνω σχέσεις προκύπτουν οι σχέσεις
στις παραπάνω σχέσεις προκύπτουν οι σχέσεις
(4.2.6) ![]() ή
ή ![]()
(4.2.7) ![]() ή
ή ![]()
Όπου αντί των του συμβολισμού Ck χρησιμοποιείται ο X(k). H σχέση (4.2.6) αποτελεί τον διακριτό μετασχηματισμό Fourier (Discrete Fourier Transform ή DFT) N-σημείων και η (4.2.7) την διακριτή σειρά Fourier (Discrete Fourier Series) ενός διακριτού σήματος.
ΠΑΡΑΔΕΙΓΜΑΤΑ:
Για το σήμα x=[1,3,2] , N=3, n=0,1,2, k=0,1,2, τα ορθομοναδιαία διανύσματα βάσης είναι:

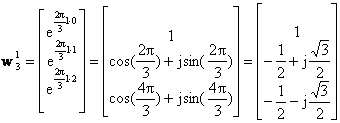
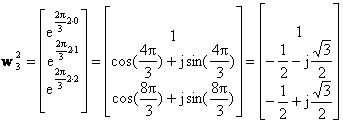

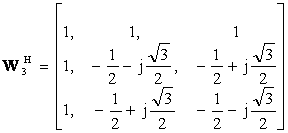
Οι τιμές ck
του DFT είναι τα
στοιχεία του πίνακα
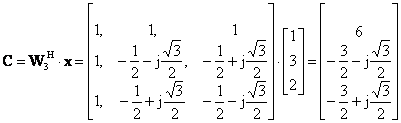
Οι τιμές του σήματος ανακτούνται από τις τιμές ck του DFT στο πίνακα
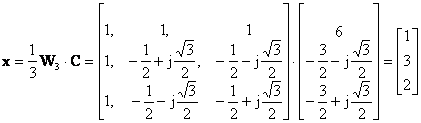
Επειδή ![]() και
και ![]() αν m=N-n, oι πίνακες W και WH είναι
συμμετρικοί ως προς την διαγώνιο και το n+1 στοιχείο μιας γραμμής ισούται με το συζυγές του Ν-n+1 στοιχείου της ίδιας
γραμμής όταν αυτό υπάρχει και ως εκ τούτου οι υπολογισμοί επιταχύνονται.
αν m=N-n, oι πίνακες W και WH είναι
συμμετρικοί ως προς την διαγώνιο και το n+1 στοιχείο μιας γραμμής ισούται με το συζυγές του Ν-n+1 στοιχείου της ίδιας
γραμμής όταν αυτό υπάρχει και ως εκ τούτου οι υπολογισμοί επιταχύνονται.
4.3 Ο μετασχηματισμός Fourier διακριτού χρόνου
Η ποσότητα ![]() , k=0..N-1, ονομάζεται κυκλική
συχνότητα και παίρνει Ν διακριτές τιμές από 0 έως (2π(Ν-1)/Ν). Για σήματα μη
πεπερασμένου μήκους το
, k=0..N-1, ονομάζεται κυκλική
συχνότητα και παίρνει Ν διακριτές τιμές από 0 έως (2π(Ν-1)/Ν). Για σήματα μη
πεπερασμένου μήκους το ![]() και η μεταβλητή ωk αντικαθίσταται από την μεταβλητή ω Î[0,2π].
Ο Μετασχηματισμός Fourier
διακριτού χρόνου (Discrete Time Fourier Transform
ή DTFT)
ορίζεται από τη σχέση:
και η μεταβλητή ωk αντικαθίσταται από την μεταβλητή ω Î[0,2π].
Ο Μετασχηματισμός Fourier
διακριτού χρόνου (Discrete Time Fourier Transform
ή DTFT)
ορίζεται από τη σχέση:
(4.3.1) ![]()
Για να υπολογιστούν οι τιμές x[n] από την (4.3.1) ενεργούμε ως ακολούθως:
Πολλαπλασιάζουμε
και τα δύο μέλη της (45) με ![]()
(4.3.2) ![]() Þ
Þ
(4.3.3) ![]()
ολοκληρώνουμε ως προς ω από -π έως π τα μέλη της ισότητας (4.3.3)
(4.3.4) 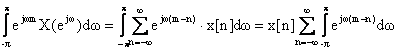
αν m=n
(4.3.5)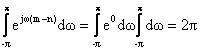
αν m¹n
(4.3.6) 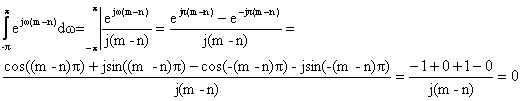
άρα η (4.3.4) γίνεται
(4.3.7) 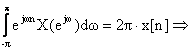
(4.3.8) 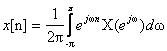
Η σχέση αυτή αποτελεί τον Aντίστροφο Mετασχηματισμός Fourier διακριτού χρόνου.
Για να ορίζεται
ο DTFT ενός σήματος
είναι προφανές ότι πρέπει το ![]() να συγκλίνει. Αυτό δεν
συμβαίνει για σήματα μη πεπερασμένου μήκους που είναι περιοδικά και ως εκ
τούτου δεν υπάρχει γι αυτά DTFT.
Αν
να συγκλίνει. Αυτό δεν
συμβαίνει για σήματα μη πεπερασμένου μήκους που είναι περιοδικά και ως εκ
τούτου δεν υπάρχει γι αυτά DTFT.
Αν ![]() περιοδικό διακριτό
σήμα με πρωτεύουσα περίοδο Ν ισχύει ότι
περιοδικό διακριτό
σήμα με πρωτεύουσα περίοδο Ν ισχύει ότι
(4.3.9) ![]()
Αν x[n] πεπερασμένου μήκους σήμα N,
(4.3.10) ![]() τότε
τότε
(4.3.11) ![]()
όπου (n mod N) το υπόλοιπο της διαίρεσης του n με το N. Ισχύει προφανώς ότι
(4.3.12) n= Nλ+ (n mod N) και 0 £ (n mod N) £ N-1 όπου λ το πηλίκο της διαίρεσης του n με το Ν.
Για το x[n] που είναι πεπερασμένου μήκους υπάρχει ο DFT και η DFS που δίνονται από τις σχέσεις (4.2.6) και (4.2.7)
Επειδή x[n]= ![]() για n=0,..,N-1 η (4.2.6) γράφεται
για n=0,..,N-1 η (4.2.6) γράφεται
(4.3.13) ![]()
και
αποτελεί την διακριτή σειρά Fourier (DFS) του ![]() . Από τις (4.3.11) και (4.2.7) προκύπτει ότι
. Από τις (4.3.11) και (4.2.7) προκύπτει ότι
![]()
(4.3.14) ![]() ή
ή ![]()
που
αποτελεί τον διακριτό μετασχηματισμό Fourier (DFT) του ![]() .
.
Άρα για τα περιοδικά διακριτά σήματα χρησιμοποιούμε τον διακριτό μετασχηματισμό Fourier (DFT) και την διακριτή σειρά Fourier DFS.
Σύμφωνα με τα παραπάνω για ένα διακριτό σήμα x(n) πεπερασμένου μήκους Ν ορίζεται και υπάρχει ο FT και ο DFT-Ν δειγμάτων σύμφωνα με τις σχέσεις
![]() ,
, ![]()
![]()
Από τις οποίες προκύπτει ότι
(4.3.15) ![]() , k=0,…,N-1
, k=0,…,N-1
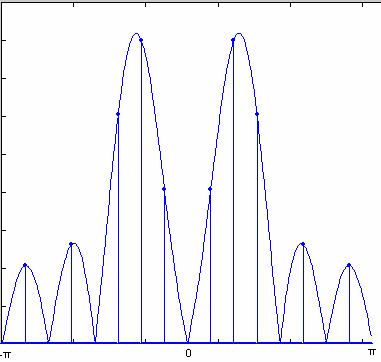
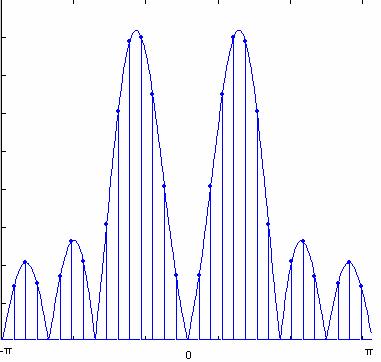
Δηλαδή ο DFT-Ν σημείων του x(n), προκύπτει από την δειγματοληψία της κυκλικής συχνότητας ω του FT του x(n) με δείγματα που απέχουν διαδοχικά μεταξύ τους απόσταση 2π/Ν. Αν αυξήσουμε το μήκος Ν προσθέτοντας μηδενικές τιμές στο τέλος του x(n), ο FT δεν θα αλλάξει θα αυξηθεί όμως το πλήθος των δειγμάτων του DFT-Ν σημείων (Σχ.4.3.1).
|
|
|
|
|
Σχήμα 4.3.1. Διάγραμμα πλάτους του FT{cos(2πn/8)} και οι DFT-Ν σημείων για Ν=8 και Ν=16 |
4.3.1 Ιδιότητες του μετασχηματισμού Fourier διακριτού χρόνου.
Από μαθηματικής απόψεως υπάρχουν ιδιότητες του FT που βοηθούν στον υπολογισμό αυτού και του αντιστρόφου του καθώς και στην περεταίρω διαδικασία ανάλυσης των σημάτων και των συστημάτων.
Περιοδικότητα
Ο DTFT είναι περιοδικός ως προς ω με περίοδο 2π. Ισχύει δηλαδή η σχέση
(4.3.1) ![]()
Συμμετρία
Ο DTFD παρουσιάζει
κάποια είδη συμμετρίας ανάλογα με το διακριτό σήμα. Τα είδη αυτά συμμετρίας
αναγράφονται στο ακόλουθο πίνακα 4.3.1.1.
|
|
|
|
Πραγματική και άρτια |
Πραγματική και άρτια |
|
Πραγματική και περιττή |
Φανταστική και περιττή |
|
Φανταστική και άρτια |
Φανταστική και άρτια |
|
Φανταστική και περιττή |
Πραγματική και άρτια |
|
Πίνακας 4.3.1.1 |
|
Γραμμικότητα
(4.3.1.2) ![]()
Ιδιότητα της Μετατόπισης
(4.3.1.3) ![]()
Αντιστροφή στο χρόνο
(4.3.1.4) ![]()
Διαμόρφωση
(4.3.1.5) ![]()
(4.3.1.6) ![]()
Το Θεώρημα της Συνέλιξης
(4.3.1.7) ![]()
Το Θεώρημα του Πολλαπλασιασμού
(4.3.1.8) ![]()
Το Θεώρημα του Parseval
(4.3.1.9) ![]()
Οι παραπάνω ιδιότητες αναγράφονται συνοπτικά στον πίνακα 4.3.1.2
|
Ιδιότητα |
Ακολουθία |
Μετασχηματισμός FOURIER διακριτού χρόνου |
|
Γραμμικότητα |
|
|
|
Μετατόπιση στο χρόνο |
|
|
|
Αντιστροφή στο χρόνο |
|
|
|
Διαμόρφωση |
|
|
|
Συνέλιξη στο χρόνο |
|
|
|
Μιγαδική συζυγία |
|
|
|
Παραγώγιση |
|
|
|
Πολλαπλασιασμός στο χρόνο |
|
|
|
Πϊνακας 4.3.1.2 |
||
Παράδειγμα 4.3.1 Ο DTFT της ακολουθίας
![]()
είναι
![]()
Με χρήση γεωμετρικών προόδων, το άθροισμα αυτό είναι
![]()
Με την προϋπόθεση ότι |α|<1. Παρόμοια, για την ακολουθία
![]()
ο DTFT είναι
![]()
Αλλάζοντας τα όρια του αθροίσματος, έχουμε
![]()
Αν είναι |α|>1, το άθροισμα είναι
![]()
Επομένως, οι ακολουθίες ![]() , έχουν τον ίδιο DTFT
, έχουν τον ίδιο DTFT
Στο πίνακα 4.3.1.3 παρουσιάζεται ο DTFT μερικών βασικών ακολουθιών
|
Ακολουθία |
Μετασχηματισμός FOURIER διακριτού
χρόνου |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Πίνακας 4.3.1.3 |
|
4.4 Σχέση της συνέλιξης με το μετασχηματισμό και τον διακριτό
μετασχηματισμό Fourier
Αν ![]() και
και ![]() περιοδικές ακολουθίες με ίδια πρωτεύουσα περίοδο Ν, η περιοδική συνέλιξη τους γράφεται και
ορίζεται σύμφωνα με την ακόλουθη σχέση:
περιοδικές ακολουθίες με ίδια πρωτεύουσα περίοδο Ν, η περιοδική συνέλιξη τους γράφεται και
ορίζεται σύμφωνα με την ακόλουθη σχέση:
(4.4.1) ![]() ή
ή ![]()
![]()
Μπορούμε να γράψουμε ακόμη ότι
(4.4.2) ![]() ,
, ![]() ,
,
με
(4.4.3)![]() ,
, ![]() ,
,
σήματα πεπερασμένου μήκους Ν.
Από τις (4.4.1) και (4.4.2) προκύπτει ότι
(4.4.4) ![]()
![]()
Δεξιό μέρος της (4.4.4) ονομάζεται κυκλική συνέλιξη δύο σημάτων πεπερασμένου μήκους Ν και γράφεται
(4.4.5)
![]() ©
©![]() =
=![]() =
=![]()
Αριθμητικά η περιοδική συνέλιξη υπολογίζεται όπως φαίνεται στο ακόλουθο παράδειγμα
Έστω
|
|
N |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
|
|
|
… |
3 |
0 |
4 |
2 |
3 |
0 |
4 |
2 |
… |
|
|
|
… |
4 |
2 |
1 |
3 |
4 |
2 |
1 |
3 |
… |
με πρωτεύουσα περίοδο Ν=4
|
|
K |
… |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
|
|
|
|
|
… |
3 |
0 |
4 |
2 |
3 |
0 |
4 |
2 |
… |
|
|
|
|
|
… |
4 |
2 |
1 |
3 |
4 |
2 |
1 |
3 |
… |
|
|
|
N=0 |
|
… |
3 |
2 |
4 |
0 |
3 |
2 |
4 |
0 |
… |
|
|
|
N=1 |
|
… |
0 |
3 |
2 |
4 |
0 |
3 |
2 |
4 |
… |
|
|
|
N=2 |
|
… |
4 |
0 |
3 |
2 |
4 |
0 |
3 |
2 |
… |
|
|
|
N=3 |
|
… |
2 |
4 |
0 |
3 |
2 |
4 |
0 |
3 |
… |
|
|
Στη
γραμμοσκιασμένη περιοχή του πίνακα φαίνονται οι τιμές που χρησιμοποιούνται για
τον υπολογισμό της κυκλικής συνέλιξης ![]() ©
©![]() και της περιοδικής συνέλιξης
και της περιοδικής συνέλιξης ![]() .
.
Η γραμμική συνέλιξη και ο DTFT δύο σημάτων συνδέονται με την σχέση:
(4.4.6) ![]()
όπου
![]() οι
μετασχηματισμοί Fourier των x(n) και y(n)
οι
μετασχηματισμοί Fourier των x(n) και y(n)
Απόδειξη

Η περιοδική συνέλιξη και ο DFT δύο περιοδικών σημάτων συνδέονται με την σχέση:
(4.4.7) ![]()
![]()
όπου![]() οι διακριτοί μετασχηματισμοί (DFΤ) των
οι διακριτοί μετασχηματισμοί (DFΤ) των ![]() και
και ![]()
Απόδειξη
Η κυκλική συνέλιξη και ο DFT δύο σημάτων πεπερασμένου μήκους Ν συνδέονται με την σχέση:
(4.4.8) ![]() ©
©![]()
![]()
όπου
![]() οι διακριτοί
μετασχηματισμοί (DFΤ-Ν
δειγμάτων) των x(n) και y(n). Η σχέση αυτή προκύπτει από τις (4.4.2) και (4.4.5)
οι διακριτοί
μετασχηματισμοί (DFΤ-Ν
δειγμάτων) των x(n) και y(n). Η σχέση αυτή προκύπτει από τις (4.4.2) και (4.4.5)
Έστω x(n) σήμα πεπερασμένου μήκους Ν1 με DFT X(k) και y(n) σήμα πεπερασμένου μήκους Ν2. Προσθέτοντας στο τέλος του x(n) πλήθος Ν2-1 μηδενικών τιμών και στο y(n) πλήθος Ν1-1 μηδενικών τιμών προκύπτουν δύο νέα σήματα xp(n) και yp(n) πεπερασμένου μήκους Ν1+ Ν2-1. H διαδικασία αυτή ονομάζεται zero padding. Εύκολα μπορούμε να δούμε με κάποιο τυχαίο παράδειγμα αλλά και να αποδείξουμε ότι γενικά:
(4.4.9)![]() = xp(n)© yp(n)
= xp(n)© yp(n)
Για παράδειγμα αν x=[2 4 1 -1 y=[1 3 2], τότε xp=[2 4 1 -1 0], yp=[1 3 2 0 0 0].
|
2 |
4 |
1 |
-1 |
x*y |
|
2 |
4 |
1 |
-1 |
0 |
0 |
xp© yp |
|
1 |
|
|
|
2 |
|
1 |
0 |
0 |
0 |
2 |
3 |
2 |
|
3 |
1 |
|
|
10 |
|
3 |
1 |
0 |
0 |
0 |
2 |
10 |
|
2 |
3 |
1 |
|
17 |
|
2 |
3 |
1 |
0 |
0 |
0 |
17 |
|
|
2 |
3 |
1 |
10 |
|
0 |
2 |
3 |
1 |
0 |
0 |
10 |
|
|
|
2 |
3 |
-1 |
|
0 |
0 |
2 |
3 |
1 |
0 |
-1 |
|
|
|
|
2 |
-2 |
|
0 |
0 |
0 |
2 |
3 |
1 |
-2 |
Με βάση τα παραπάνω, αν Xp(k) και Υp(k) οι DFT των xp(n) και yp(n x(n) αντίστοιχα θα ισχύει ότι:
(4.4.10) ![]() = xp(n)© yp(n
= xp(n)© yp(n![]()
(4.4.11) ![]()
![]()
ΚΕΦΑΛΑΙΟ 5
Ανάλυση σημάτων και συστημάτων με τον
μετασχηματισμό Fourier
Ο μετασχηματισμός Fourier (DTFT και DFT) είναι σημαντικότατος για την ανάλυση των σημάτων και των συστημάτων. Οι συχνότητες των αρμονικών ταλαντώσεων ( συχνοτικό περιεχόμενο) που ενυπάρχουν σε ένα σήμα ευρίσκονται μέσω του FT. H επίδραση ενός συστήματος στο συχνοτικό περιεχόμενο του σήματος εισόδου, αναλύεται επίσης μέσω του FT και προσδιορίζεται το συχνοτικό περιεχόμενο του σήματος εξόδου. Ο σχεδιασμός συστημάτων (φίλτρα) με επιθυμητή επίδραση βασίζεται στον FT.
Ας θεωρήσουμε ένα σύστημα γραμμικό ανεξάρτητο από τη μετατόπιση με απόκριση κρουστικής διέγερσης h(n). Η έξοδος του για οποιοδήποτε είσοδο x(n) θα είναι
y(n)=x(n)*h(n)
Σύμφωνα με το θεώρημα της συνέλιξης ισχύει ότι
![]()
όπου Η(ejω)=DTFT{ h(n)}. H Η(ejω) ονομάζεται απόκριση συχνότητας του συστήματος και καθορίζει την επίδραση του συστήματος στο DTFT του σήματος εισόδου. Με άλλα λόγια η απόκριση συχνότητας καθορίζει την επίδραση του συστήματος στο συχνοτικό περιεχόμενο του σήματος εισόδου. Η Η(ejω) παίρνει μιγαδικές τιμές και ως εκ τούτου μπορεί να γραφεί με το πλάτος | Η(ejω)| και τη φάση της φ(ω) σύμφωνα με τη σχέση
Η(ejω)=| Η(ejω)|∙ej∙φ(ω)
Η μελέτη της απόκρισης συχνότητας αφορά τον υπολογισμό και τη γραφική παράσταση του πλάτους και της φάση της. Συχνά μελετάται και καθυστέρηση ομάδας (group delay) τ(ω) που ορίζεται ως
![]()
Όταν η φάση φ(ω) είναι μια γραμμική συνάρτηση του ω, το σύστημα λέγεται σύστημα γραμμικής φάσης.
Παράδειγμα 5.2.1
Έστω το σύστημα y(n)= 0.5∙x(n-1)+x(n)+0.5∙x(n+1), να υπολογισθούν το πλάτος και φάση της απόκρισης συχνότητας και να γίνουν οι γραφικές τους παραστάσεις.
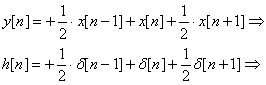
![]()
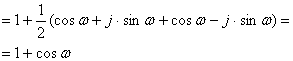
![]()
|
|
|
Η γραφική παράσταση του πλάτους |Η(ejw)| της απόκρισης συχνότητας |
Το
σύστημα είναι ένα κατωδιαβατό ή χαμηλοπερατό φίλτρο.
Παράδειγμα 5.2.2
Έστω το σύστημα y(n)= 0.5∙x(n-1))+0.5∙x(n-2), να υπολογισθούν το πλάτος και φάση της απόκρισης συχνότητας και να γίνουν οι γραφικές τους παραστάσεις.
![]()
![]()
![]() ,
, ![]() ,
, ![]()
Στο ακόλουθο σχήμα φαίνονται τα
διαγράμματα πλάτους και φάσης της απόκρισης συχνότητας του συστήματος.
|
|
|
|
|
|
Το σύστημα είναι
γραμμικής φάσης. Η παράγωγος του είναι σταθερός αριθμός συνεπώς η καθυστέρηση
ομάδας που δείχνει την καθυστέρηση (σε πλήθος δειγμάτων) που υφίσταται το σήμα
εισόδου από το σύστημα είναι η ίδια για κάθε τιμή του ω.
Παράδειγμα 5.2.3 Θεωρούμε το LTI σύστημα με κρουστική απόκριση
![]()
όπου α, ένας πραγματικός αριθμός με |α|<1. Η απόκριση συχνότητας είναι

Το τετράγωνο του πλάτους της απόκρισης συχνότητας είναι
![]()
και η φάση είναι
![]()
Τέλος, η καθυστέρηση ομάδας υπολογίζεται παραγωγίζοντας την συνάρτηση της φάσης. Το αποτέλεσμα είναι
![]()
5.2.1 Φίλτρα επιλογής συχνοτήτων
Ανάλογα με την μεταβολή του
πλάτους της απόκρισης συχνότητας σε σχέση με την συχνότητα τα συστήματα
διακρίνονται στις ακόλουθες κατηγορίες:
Χαμηλοπερατά (Low pass): Το πλάτος έχει μεγάλες
τιμές για χαμηλές τιμές της συχνότητας και μικρές τιμές για υψηλές τιμές της
συχνότητας. Στην ιδανική περίπτωση το πλάτος της απόκρισης συχνότητας
μεταβάλλεται όπως στο Σχ.5.2.1
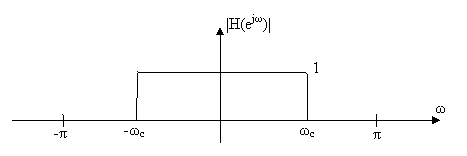
Σχήμα 5.2.1: Ιδανικό Χαμηλοπερατό Φίλτρο (Low-Pass)
Υψηπερατά (High pass): Το πλάτος έχει μεγάλες τιμές για υψηλές τιμές της συχνότητας και μικρές τιμές για χαμηλές τιμές της συχνότητας. Στην ιδανική περίπτωση το πλάτος της απόκρισης συχνότητας μεταβάλλεται όπως στο Σχ.5.2.2.
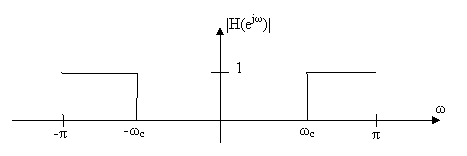
Σχήμα 5.2.2: Ιδανικό Υψηπερατό Φίλτρο (High-Pass)
Ζωνοπερατά (Band pass): Το πλάτος έχει μεγάλες τιμές σε μία ζώνη τιμών της συχνότητας και μικρές τιμές εκτός της ζώνης αυτής. Στην ιδανική περίπτωση το πλάτος της απόκρισης συχνότητας μεταβάλλεται όπως στο Σχ.5.2.3.
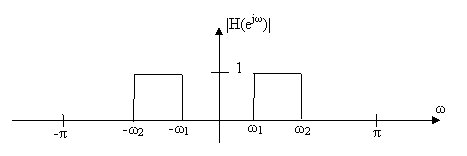
Σχήμα 5.2.3: Ιδανικό Ζωνοπερατό Φίλτρο (Band-Pass)
Ζωνοφρακτικά (Band stop): Το πλάτος έχει μικρές τιμές σε μία ζώνη τιμών της συχνότητας και μεγάλες τιμές εκτός της ζώνης αυτής. Στην ιδανική περίπτωση το πλάτος της απόκρισης συχνότητας μεταβάλλεται όπως στο Σχ.5.2.4.
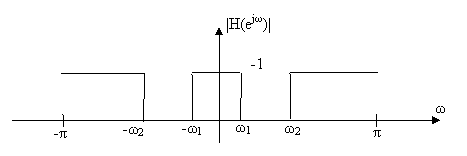
Σχήμα 5.2.4: Ιδανικό Ζωνοφρακτικό Φίλτρο (Band-Stop)
5.3 Ανάλυση της δειγματοληψίας
Ο μετασχηματισμός Fourier και η περιοδικότητα των ημιτονοειδών διακριτών σημάτων οδηγούν σε σημαντικά συμπεράσματα για την δειγματοληψία των αναλογικών σημάτων. Θα ξεκινήσουμε την παρουσίαση της ανάλυσης της δειγματοληψίας με παρουσίαση των χαρακτηριστικών των ημιτονοειδών διακριτών σημάτων. Ένα διακριτό ημιτονοειδές σήμα είναι της μορφής
![]() (5.3.1)
(5.3.1)
όπου Α το πλάτος, θ η φάση και ω η κυκλική συχνότητά του. Επειδή η ανεξάρτητη μεταβλητή είναι ένα ακέραιος αριθμός που απαριθμεί τις διαδοχικές τιμές των δειγμάτων η κυκλική συχνότητα μετριέται σε ακτίνια ανά δείγμα (radians per sample). Η κυκλική συχνότητα στα ημιτονοειδή σήματα συνεχούς μεταβλητής μετριέται σε ακτίνια ανά δευτερόλεπτο επειδή αρχικά τα σήματα αυτά αφορούσαν αρμονικές ταλαντώσεις όπου η συνεχής μεταβλητή είναι ο χρόνος. Αντίστοιχα η ποσότητα f που ικανοποιεί τη σχέση
![]() , (5.3.2)
, (5.3.2)
![]() (5.3.3)
(5.3.3)
αποτελεί την συχνότητα του διακριτού ημιτονοειδούς σήματος και μετριέται σε κύκλους ανά δείγμα (circles per sample). Από τις σχέσεις (5.3.1) και (5.3.2) προκύπτει ότι
![]() (5.3.4)
(5.3.4)
Τα ημιτονοειδή σήματα xa(t)=Α∙cos(Ω∙t+θ) συνεχούς χρόνου με κυκλική συχνότητα Ω (rad/sec) είναι περιοδικά με περίοδο Τ=2π/Ω (sec), συχνότητα F=1/T (sec-1 ή Hz) . Το ερώτημα είναι αν και πότε τα διακριτά ημιτονοειδή σήματα είναι περιοδικά.. Προς τούτο αν Ν η πρωτεύουσα περίοδος πρέπει να ισχύουν οι ακόλουθος σχέσεις:
x(n)=x(n+N (5.3.5)
![]() , k ακέραιος (5.3.6)
, k ακέραιος (5.3.6)
![]() (5.3.7)
(5.3.7)
Άρα η περιοδικότητα εξασφαλίζεται αν
![]() (5.3.8)
(5.3.8)
δηλαδή f να είναι ρητός αριθμός.
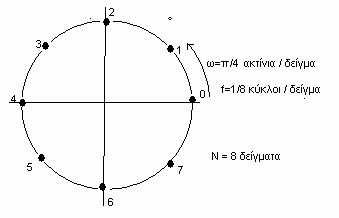
Η πρωτεύουσα περίοδος Ν είναι θετικός ακέραιος πρώτος προς τον k, (δηλαδή δεν έχουν κοινούς διαιρέτες). Για παράδειγμα αν Α=1, θ=0 ακτίνια, f=1/8 κύκλοι ανά δείγμα η κυκλική συχνότητα είναι ω=π/4 ακτίνια ανά δείγμα και η περίοδος Ν=8
![]()
![]()
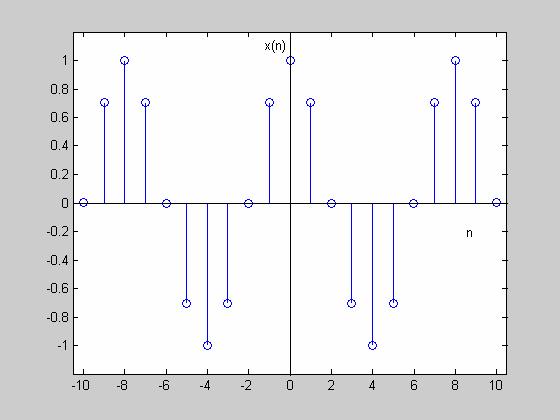
Στο Σχ.5.3.1 φαίνονται οι τιμές των n, f και ω στον τριγωνομετρικό κύκλο και το σήμα x(n). Αν Α=1 και θ=0 ακτίνια, f=9/8 κύκλοι ανά δείγμα η κυκλική συχνότητα είναι ω=9π/4 ακτίνια ανά δείγμα και η πρωτεύουσα περίοδος Ν=8,
![]()
Παρατηρούμε
ότι αν και οι τιμές της συχνότητας είναι διαφορετικές τα σήματα είναι ίσα.
Γενικά αν x(n)=cos(ω0∙n) με κυκλική συχνότητα ω0
![]() (5.3.9)
(5.3.9)
|
|
|
|
|
Σχήμα 5.3.1 |
κάθε διακριτό σήμα x΄(n)=cos(ω∙n) με κυκλική συχνότητα
ω=ω0+2kπ (5.3.10)
όπου k ακέραιος, είναι ίσο με το x(n). Για τις συχνότητες f0 και f θα ισχύουν οι σχέσεις
![]() (5.3.11)
(5.3.11)
![]() (5.3.12)
(5.3.12)
![]() (5.3.13)
(5.3.13)
Συνεπώς
όλα τα διακριτά ημιτονοειδή σήματα μπορούν να περιγραφούν με τιμές της
συχνότητας f0 στο διάστημα [-½,½]
(αντίστοιχα της κυκλικής συχνότητας ω0
στο διάστημα [-π,π] ). Κάθε ημιτονοειδής ακολουθία x΄(n) με συχνότητα f εκτός
του διαστήματος αυτού ( | f |
> ½ , | ω | > π ) είναι ίδια με κάποια
ακολουθία x(n) που έχει
συχνότητα εντός του διαστήματος [-½,½]. Η ακολουθία x΄(n) θα ονομάζεται ψευδώνυμη
(alias) της x(n) και το
φαινόμενο αυτό ψευδωνυμία (aliasing). Τα διαστήματα
[-½,½], [-π, π] λέγονται θεμελιώδη
διαστήματα της συχνότητας και της κυκλικής συχνότητας των διακριτών
ημιτονοειδών σημάτων αντίστοιχα. Η συχνότητα f της
ψευδώνυμης διαφέρει από την συχνότητα f0 κατά
ακέραιο αριθμό (σχέση 5.3.12) , Η συχνότητα ω της ψευδώνυμης διαφέρει από την
συχνότητα ω0 κατά ακέραιο πολλαπλάσιο του 2π (σχέση 5.3.10).
Ο πιο συνήθης τρόπος μετατροπής ενός αναλογικού σήματος σε διακριτό είναι η περιοδική ή ομοιόμορφη δειγματοληψία. Λαμβάνονται δείγματα του σήματος σε διαδοχικές τιμές της ανεξάρτητης μεταβλητής. Η απόσταση δύο διαδοχικών τιμών είναι σταθερή και ονομάζεται διάστημα δειγματοληψίας. Αν η ανεξάρτητη μεταβλητή είναι ο χρόνος t, το διάστημα δειγματοληψίας Ts μετριέται σε δευτερόλεπτα (sec). Το πλήθος τον δειγμάτων σε ένα δευτερόλεπτο λέγεται ρυθμός ή συχνότητα δειγματοληψίας
![]() ,
, ![]() (5.3.14)
(5.3.14)
και μετριέται σε δείγματα ανά δευτερόλεπτο (samples per second). Αν το συνεχές σήμα είναι ημιτονοειδές με κυκλική συχνότητα Ω rad/sec, περίοδο Τ sec, συχνότητα F sec-1 (Hz) και δίνεται από την σχέση
![]() (5.3.15)
(5.3.15)
από την περιοδική δειγματοληψία του προκύπτει η ακολουθία x(n) σύμφωνα με την σχέση
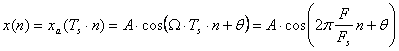 (5.3.16)
(5.3.16)
Η συχνότητα του x(n) είναι
![]() (5.3.17)
(5.3.17)
Άρα η συχνότητα του συνεχούς που ανακτάται είναι
![]() (5.3.18)
(5.3.18)
Επειδή η f ανήκει στο διάστημα [-½ , ½ ] πρέπει
![]()
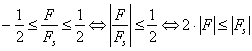 (5.3.19)
(5.3.19)
Αν το συνεχές σήμα ήταν το
![]() (5.3.20)
(5.3.20)
με συχνότητα
F΄=F+kFs (5.3.21)
από την δειγματοληψία του με ρυθμό Fs θα προκύψει το διακριτό σήμα
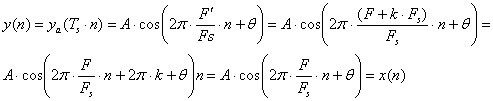 (5.3.22)
(5.3.22)
Άρα τα συνεχή σήματα xa(t) και ya(t) μετά από την παραπάνω δειγματοληψία παριστάνονται από την ίδια ακολουθία x(n). Το γεγονός αυτό οφείλεται στο ότι η συχνότητα του διακριτού σήματος y(n) είναι ψευδώνυμη της συχνότητας του διακριτού σήματος x(n). Πράγματι η συχνότητα f΄ του σήματος y(n) ισούται με
![]() (5.3.23)
(5.3.23)
Για να μη είναι δυνατή η ψευδωνυμία και να μπορεί να ανακτηθεί με μοναδικό τρόπο το αρχικό συνεχές σήμα πρέπει να ισχύει η σχέση (5.3.19) Που για θετικές τιμες των συχνοτήτων γράφεται
![]() (5.3.24)
(5.3.24)
Άσκηση
Έστω το συνεχές σήμα xα(t)=cos(100π∙t)
Α) Να βρεθεί η ελάχιστη τιμή της συχνότητας δειγματοληψίας ώστε να αποφευχθεί η ψευδωνυμία.
Β) Αν ο ρυθμός δειγματοληψίας είναι 200 Ηz, ποιο το διακριτό σήμα που θα προκύψει;
Γ) Αν ο ρυθμός δειγματοληψίας είναι 75 Ηz, ποιο το διακριτό σήμα που θα προκύψει;
Δ) Ποια η τιμή της συχνότητας ενός συνεχούς σήματος συνημιτόνου που μετά από σωστή δειγματοληψία δίνει διακριτό σήμα ίδιο με αυτό που προκύπτει στο ερώτημα Γ.
Απαντήσεις
Α) F=100π/2π = 50 Ηz, άρα η ελάχιστη τιμή της συχνότητας δειγματοληψίας είναι Fs=100 Hz (δείγματα / δευτερόλεπτο).
Β)
![]()
Γ) ![]()
Δ)
![]() H συχνότητα του διακριτού σήματος x(n) του ερωτήματος Γ είναι f=2/3=-1/3+1 και ως εκ
τούτου είναι ψευδώνυμη της
H συχνότητα του διακριτού σήματος x(n) του ερωτήματος Γ είναι f=2/3=-1/3+1 και ως εκ
τούτου είναι ψευδώνυμη της ![]() . Άρα η συχνότητα F του
ζητούμενου αναλογικού σήματος ικανοποιεί τη σχέση F/75=1/3 άρα
F=25Ηz.
. Άρα η συχνότητα F του
ζητούμενου αναλογικού σήματος ικανοποιεί τη σχέση F/75=1/3 άρα
F=25Ηz.
----
Ένα σήμα συνεχούς μεταβλητής ορισμένο σε ένα διάστημα [α,β] είναι δυνατόν να αναπαρασταθεί «καλά» με την ανάλυση Fourier ως άθροισμα αρμονικών ταλαντώσεων σύμφωνα με τη σχέση
![]() (5.3.25)
(5.3.25)
Η
ωφέλιμη πληροφορία του σήματος είναι δυνατόν να φέρεται στα πλάτη Αk, τις συχνότητες Fk ή τις φάσεις
θk. Εν τούτοις, αν![]() για να αποφύγουμε το φαινόμενο της ψευδωνυμίας κατά την
δειγματοληψία του xa(t), πρέπει
ο ρυθμός δειγματοληψίας να είναι τουλάχιστον 2∙Fmax. H ποσότητα αυτή
ονομάζεται ρυθμός Nyquist συμβολίζεται FN και ισχύσει
για να αποφύγουμε το φαινόμενο της ψευδωνυμίας κατά την
δειγματοληψία του xa(t), πρέπει
ο ρυθμός δειγματοληψίας να είναι τουλάχιστον 2∙Fmax. H ποσότητα αυτή
ονομάζεται ρυθμός Nyquist συμβολίζεται FN και ισχύσει
FN =2∙Fmax. (5.3.26)
Το θεώρημα της δειγματοληψίας. Αν η μεγαλύτερη απολύτως συχνότητα που περιέχεται σε ένα αναλογικό σήμα xa(t) είναι Fmax=B και το σήμα δειγματοληπτείται με ρυθμό Fs> 2∙Fmax =2∙B, τότε το xa(t) μπορεί να ανακατασκευασθεί επακριβώς από τα δείγματά του με χρήση της συνάρτησης παρεμβολής
![]() (5.3.27)
(5.3.27)
Σύμφωνα με τη σχέση
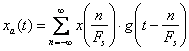 (5.3.28)
(5.3.28)
Άσκηση
Έστω το αναλογικό σήμα xa(t)=2∙cos(50π∙t)+sin(200π∙t)-5∙cos(70π∙t), ποιος ο ρυθμός Nyquist FN;
F1=25 Hz, F2=100
Hz, F3=35 Hz
Fmax=100 Hz άρα FN= 200 Hz
Παρατήρηση: Αν το σήμα sin(200π∙t) δειγματοληπτηθεί με συχνότητα δειγματοληψίας Fs= FN, το διακριτό σήμα είναι sin(π∙n)=0 και ως εκ τούτου δεν μπορεί να ανακτηθεί το αρχικό συνεχές σήμα. Ένας τρόπος να υπερβούμε το πρόβμημα αυτό είναι ο ρυθμός δειγματοληψίας να είναι Fs> FN.
Ο Μετασχηματισμός Ζ
Ο
μετασχηματισμός Z (Ζ-Τransform: ZT) αποτελεί ένα χρήσιμο μαθηματικό
εργαλείο για την ανάλυση των διακριτών σημάτων και συστημάτων και αποτελεί για
αυτά ότι ο μετασχηματισμός Laplace για τα σήματα και σύστημα
συνεχούς μεταβλητής. Η χρήση του στην επίλυση γραμμικών εξισώσεων
διαφορών με σταθερούς συντελεστές βοηθά στην ανάλυση συστημάτων που
περιγράφονται αναδρομικά. Ο υπολογισμός της απόκρισης και ο έλεγχος της
ευστάθειας των γραμμικών ανεξάρτητων από τη μετατόπιση συστημάτων είναι δυνατόν
επιτευχθεί με την χρήση του ZT.
6.2 Ορισμός του μετασχηματισμού Ζ
Ο μετασχηματισμός Ζ μιας ακολουθίας x(n) ορίζεται και γράφεται ως ακολούθως:
![]()
![]() ,
, ![]() ,
, ![]() (6.2.1)
(6.2.1)
Οι τιμές του της μιγαδικής μεταβλητής z για τις οποίες συγκλίνει το άθροισμα του μετασχηματισμού ονομάζεται περιοχή σύγκλισης ή ΠΣ (Region Of Convergence ή ROC).
Αν θέσουμε ![]() , r=|z|
, r=|z|
![]() (6.2.2)
(6.2.2)
και
αν θέσουμε ![]()
![]() (6.2.3)
(6.2.3)
6.2.1 Ιδιότητες του μετασχηματισμού Ζ
Ισχύουν οι ακόλουθες ιδιότητες του ΖT που βοηθούν στον υπολογισμό αυτού και του αντιστρόφου του καθώς και στην περεταίρω διαδικασία ανάλυσης των σημάτων και των συστημάτων.
Ιδιότητα της
μετατόπισης
![]() (6.2.1.1)
(6.2.1.1)
Αντιστροφή στο χρόνο
![]() (6.2.1.2)
(6.2.1.2)
Πολλαπλασιασμός με
εκθετικό ορό
![]() (6.2.1.3)
(6.2.1.3)
![]() (6.2.1.4)
(6.2.1.4)
Το θεώρημα της
συνέλιξης
![]() (6.2.1.5)
(6.2.1.5)
Μιγαδική συζυγία
![]() (6.2.1.6)
(6.2.1.6)
![]() (6.2.1.7)
(6.2.1.7)
Παράγωγος
![]() (6.2.1.8)
(6.2.1.8)
Θεώρημα αρχικής τιμής
![]() (6.2.1.9)
(6.2.1.9)
![]() (6.2.1.10)
(6.2.1.10)
Οι παραπάνω ιδιότητες αναγράφονται συνοπτικά στον Πίν. 6.2.1
Ιδιότητες του Μετασχηματισμού z
|
Ιδιότητα |
Ακολουθία |
Μετασχηματισμός z |
Περιοχή σύγκλισης |
|
Γραμμικότητα |
|
|
Περιέχει |
|
Μετατόπιση |
|
|
|
|
Αντιστροφή στο χρόνο |
|
|
|
|
Πολλαπλασιασμός με εκθετική ακολουθία |
|
|
|
|
Συνέλιξη |
|
|
Περιέχει |
|
Μιγαδική συζυγία |
|
|
|
|
Παράγωγος |
|
|
|
|
Πίνακας 6.2.1 |
|||
Στο Πιν. 6.2.2. παρουσιάζεται ο ΖΤ μερικών βασικών ακολουθιών
|
Ακολουθία |
Μετασχηματισμός |
Περιοχή σύγκλισης |
|
|
1 |
Όλες οι τιμές του Ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Πίνακας 6.2.2 |
||
Ανάλυση συστημάτων με τον μετασχηματισμό
Ζ
Όπως
αναφέρθηκε σε προηγούμενο κεφάλαιο η έξοδος ενός LTI συστήματος
σε οποιαδήποτε είσοδο x(n) μπορεί
να υπολογισθεί από την συνέλιξη (συνελικτικό άθροισμα) της εισόδου με την
κρουστική απόκριση h(n) του
συστήματος. Με χρήση του θεωρήματος της συνέλιξης όπως ισχύει για τον
μετασχηματισμό Ζ ισχύει η σχέση
![]() (7.1.1)
(7.1.1)
Η συνάρτηση Η(z) που είναι ο μετασχηματισμός Ζ της h(n), ονομάζεται συνάρτηση μεταφοράς (system function) του συστήματος. Από την μελέτη της συνάρτησης μεταφοράς ενός LTI είναι δυνατόν να χαρακτηρισθεί αυτό ως προς την αιτιότητα, την ευστάθεια και άλλα χαρακτηριστικά του και να μελετηθούν διάφοροι ειδικοί τύποι LTI όπως συστήματα γραμμικής και ελάχιστης φάσης, φίλτρα και κυκλώματα ανάδρασης. Ακόμη, με τον μετασχηματισμό Ζ διευκολύνεται και βελτιστοποιείται ο σχεδιασμός ενός συστήματος.
Σύμφωνα με τα προηγούμενα αν h(n) η κρουστική απόκριση ενός LTI η συνάρτηση μεταφοράς του δίνεται από τη σχέση
![]() (7.2.1)
(7.2.1)
Από την σχέση 7.1.1 προκύπτει ότι η συνάρτηση μεταφορά μπορεί να υπολογισθεί από την σχέση
![]() (7.2.2)
(7.2.2)
Για
παράδειγμα η συνάρτηση μεταφοράς του ακόλουθου LTI συστήματος ![]() , μπορεί να βρεθεί με χρήση της ιδιότητας μετατόπισης του ΖΤ.
Παίρνοντας τους ΖΤ της εξίσωσης του συστήματος έχουμε ότι
, μπορεί να βρεθεί με χρήση της ιδιότητας μετατόπισης του ΖΤ.
Παίρνοντας τους ΖΤ της εξίσωσης του συστήματος έχουμε ότι ![]() Γενικά για ένα LTI σύστημα που περιγράφεται από
τη σχέση
Γενικά για ένα LTI σύστημα που περιγράφεται από
τη σχέση
![]() (7.2.3)
(7.2.3)
η συνάρτηση μεταφοράς θα
είναι
 (7.2.4)
(7.2.4)
Με ανάλυση σε γινόμενο παραγόντων των πολυωνύμων αριθμητή και παρονομαστή η συνάρτηση μεταφοράς είναι
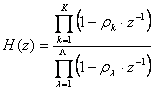 (7.2.5)
(7.2.5)
όπου ρκ και ρλ οι ρίζες των πολυωνύμων λαμβανομένης υπ’ όψη της πολλαπλότητας τους. Σε μία ρητή συνάρτηση μεταφοράς, δηλαδή ένα πηλίκο πολυωνύμων της μιγαδικής μεταβλητής z, οι ρίζες του αριθμητή λέγονται μηδενικά και του παρονομαστή πόλοι. Στο μιγαδικό επίπεδο τα μηδενικά σημειώνονται με το σύμβολο «o» και οι πόλοι με το σύμβολο «x». Η εύρεση της κρουστικής απόκρισης ενός LTI συστήματος από την συνάρτηση μεταφοράς απαιτεί απλά την εύρεση του αντίστροφου μετασχηματισμού Ζ αυτής.
7.3
Έλεγχος της αιτιότητας και της ευστάθειας LTI συστήματος
Όπως αναφέρθηκε η κρουστική απόκριση h(n) ενός αιτιατού συστήματος είναι ακολουθία δεξιάς πλευράς, δηλαδή h(n)=0 για n<0. Ως εκ τούτου η συνάρτηση μεταφοράς H(z) θα δίνεται από τη σχέση
![]()
αν
![]() τότε
τότε ![]() συγκλίνει και
συγκλίνει και ![]() για n>n0. Αν z2 μιγαδικός
με |z2|>|z1| τότε
για n>n0. Αν z2 μιγαδικός
με |z2|>|z1| τότε ![]() και
και ![]() συγκλίνει. Άρα στη
περιοχή σύγκλισης ανήκει το μέρος του μιγαδικού επιπέδου που βρίσκεται έξω από
τον κύκλο που ορίζει την περιοχή σύγκλισης. Συμπέρασμα η
περιοχή σύγκλισης της συνάρτησης μεταφοράς ενός αιτιατού LTI συστήματος είναι όλη η περιοχή του μιγαδικού επιπέδου έξω από
τον κύκλο των εσωτερικών ορίων της.
συγκλίνει. Άρα στη
περιοχή σύγκλισης ανήκει το μέρος του μιγαδικού επιπέδου που βρίσκεται έξω από
τον κύκλο που ορίζει την περιοχή σύγκλισης. Συμπέρασμα η
περιοχή σύγκλισης της συνάρτησης μεταφοράς ενός αιτιατού LTI συστήματος είναι όλη η περιοχή του μιγαδικού επιπέδου έξω από
τον κύκλο των εσωτερικών ορίων της.
Ικανή και αναγκαία συνθήκη για την ΒΙΒΟ ευστάθεια ενός συστήματος είναι
![]() . Αν |z|=1 τότε
. Αν |z|=1 τότε ![]() .
.
Αν
λοιπόν ένα σύστημα είναι ΒΙΒΟ ευσταθές τότε πρέπει ο μοναδιαίος κύκλος ανήκει
στη περιοχή σύγκλισης. Αντίστροφα, αν ο μοναδιαίος κύκλος ανήκει στη περιοχή
σύγκλισης ενός LTI συστήματος τότε αυτό είναι BIBO ευσταθές. Συμπέρασμα,
ένα LTI σύστημα είναι ΒΙΒΟ ευσταθές αν και μόνο αν η περιοχή
σύγκλισης της συνάρτησης μεταφοράς περιλαμβάνει τον μοναδιαίο κύκλο.
Από τα παραπάνω συνάγεται ότι ικανή και αναγκαία συνθήκη για να είναι ένα σύστημα αιτιατό και ευσταθές είναι όλοι οι πόλοι του να βρίσκονται στο εσωτερικό του μοναδιαίου κύκλου. Ένα σύστημα που είναι αιτιατό και ευσταθές λέγεται πραγματοποιήσιμο σύστημα.
Αν ο παρονομαστής της ρητής συνάρτησης μεταφοράς είναι δευτέρου βαθμού είναι δυνατόν να ελέγξουμε αν οι ρίζες του (πόλοι) είναι εντός του μοναδιαίου κύκλου χωρίς να τις υπολογίσουμε, σκεπτόμενοι ως ακολούθως. Γραφουμε την συνάρτηση μεταφοράς έτσι ώστε το πολυώνυμο του παρονομαστή να είναι
![]()
Ρίζες είναι οι τιμές του z για τις οποίες D(z)=0, ήτοι
![]()
Για
τις ρίζες ρ1, ρ2 του τριωνύμου ισχύει ότι ![]()
Η
διακρίνουσα του τριωνύμου ![]() είναι
είναι
![]()
Αν Δ<0, τότε το τριώνυμο έχει δύο ρίζες ρ1, ρ2 συζυγείς μιγαδικές και ισχύει ότι
![]() .
.
Για ![]()
![]()
Αν Δ≥0, τότε οι δύο ρίζες ρ1, ρ2 είναι πραγματικές.
Για
![]()
![]() και
και ![]()
Άρα για να βρίσκονται οι
ρίζες του τριωνύμου εντός του μοναδιαίου κύκλου πρέπει να ικανοποιούνται οι
τρεις σχέσεις
![]() ,
, ![]() και
και ![]()
Στο καρτεσιανό επίπεδο με
οριζόντιο άξονα τις τιμές του α1
και κάθετο άξονα τις τιμές του α2,
το σύστημα είναι πραγματοποιήσιμο όταν το σημείο (α1, α2) βρίσκεται στο εσωτερικό του τριγώνου ευστάθειας όπως αυτό δείχνεται
στο Σχ.7.3.1
|
|
|
Σχημα 7.3.1 |
Υλοποίηση συστημάτων διακριτού χρόνου
Ένα
LTI σύστημα
μπορεί να περιγραφεί με περισσότερους από ένα τρόπο. Για παράδειγμα το σύστημα
y(n)=a1∙y(n-1)+b0∙x(n)+b1∙x(n-1)
μπορεί να περιγραφεί από τις σχέσεις
w(n)= a1∙w(n-1)+x(n)
y(n)=b0∙w(n)+b1∙w(n-1)
Στην δεύτερη περίπτωση περιγραφής του συστήματος απαιτείται μία μόνο θέση μνήμης για την αποθήκευση της τιμής w(n-1) ενώ στην πρώτη απαιτούνται δύο θέσεις για την αποθήκευση των τιμών x(n-1) και y(n-1). Η τρόπος περιγραφής ενός συστήματος επηρεάζει συχνά τον απαιτούμενο χώρο μνήμης, την ταχύτητα, το σφάλμα κβαντισμού ενός ψηφιακού συστήματος και ως εκ τούτου είναι αντικείμενο μελέτης. Στο κεφάλαιο αυτό θα παρουσιασθεί επίσης ο διαγραμματικός τρόπος περιγραφής ενός συστήματος (ψηφιακά δικτυώματα) που υποβοηθά την κυκλωματική υλοποίηση και συχνά την ανάλυση του.
Το ψηφιακό δικτύωμα είναι ένα γράφημα με
δομικά στοιχεία κλάδους και κόμβους. Οι κλάδοι είναι βέλη με μία είσοδο και μία
έξοδο και λειτουργούν ως τελεστές πολλαπλασιασμού ή καθυστέρησης. Οι κλάδοι μπορούν
να συνδεθούν μεταξύ τους με κόμβους που είναι αθροιστές ή διακλαδωτές. Στους
κόμβους άθροισης υπάρχουν δύο κλάδοι άφιξης και ένα αναχώρησης, στους κόμβους
διακλάδωσης υπάρχει ένας κλάδος άφιξης και δύο αναχώρησης. Στο Σχ. 8.2.1
φαίνονται τα δομικά στοιχεία ενός ψηφιακού δικτυώματος που περιγράφει το
σύστημα y(n)=a1∙y(n-1)+b0∙x(n)
|
|
|
Σχήμα 8.2.1 |
8.3 Περιγραφή συστημάτων FIR
Για ένα FIR σύστημα με έξοδο y(n) και κρουστική απόκριση h(n) ισχύουν οι σχέσεις
![]() (8.3.1)
(8.3.1)
![]() (8.3.2)
(8.3.2)
Από τις 8.3.1 και 8.3.2 προκύπτει ότι
![]() (8.3.3)
(8.3.3)
Η συνάρτηση μεταφοράς H(z) θα δίνεται από τη σχέση
![]() (8.3.4)
(8.3.4)
Το ψηφιακό δικτύωμα ενός τέτοιου συστήματος φαίνεται στο Σχ.8.3.1.
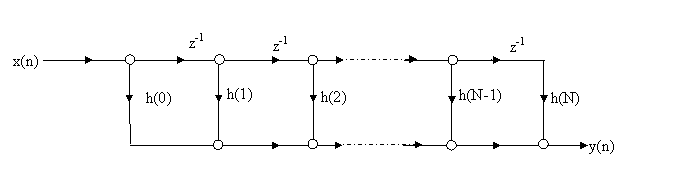
Σχήμα 8.3.1.
Ο τρόπος αυτός αλγεβρικής και διαγραμματικής περιγραφής του συστήματος λέγεται ευθεία μορφή.
Για παράδειγμα το σύστημα y(n)=2∙x(n)+4∙x(n-1)+3∙x(n-2)+x(n-3) με κρουστική απόκριση h(n)=2∙δ(n)+4∙δ(n-1)+3∙δ(n-2)+δ(n-3) και συνάρτηση μεταφοράς H(z)=2+4∙z-1+3∙z-2+ z-3 υλοποιείται διαγραμματικά όπως φαίνεται στο Σχ. 8.3.2.
Σχήμα 8.3.2
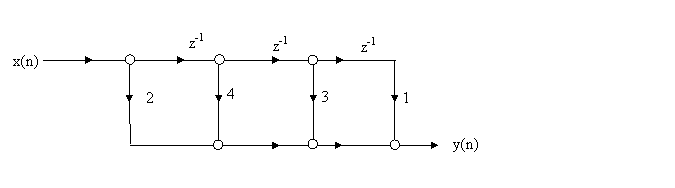
Εκτός από την ευθεία μορφή ένα FIR σύστημα μπορεί να περιγραφεί με σύνδεση σε σειρά απλούστερων (μικρότερης τάξης) FIR συστημάτων. Προς τούτο παραγοντοποιούμε την συνάρτηση μεταφοράς και εκμεταλλευόμαστε την συνελικτική και προσεταιριστική ιδιότητα του μετασχηματισμού Ζ. Ο τρόπος αυτός περιγραφής του συστήματος λέγεται μορφή καταρράκτη. Για παράδειγμα το σύστημα y(n)=2∙x(n)+4∙x(n-1)+3∙x(n-2)+x(n-3) που περιγράφηκε πιο πάνω με ευθεία μορφή έχει συνάρτηση μεταφοράς H(z)=2+4∙z-1+3∙z-2+ z-3 . Αν παραγοντοποιήσουμε την H(z) ισχύει
H(z)=2+4∙z-1+3∙z-2+ z-3=(2+2∙z-1+z-2)∙( 1+z-1)
H(z)= H1(z)∙ H2(z)
h(n)=h1(n)* h2(n)
Άρα το σύστημα αποτελείται από δύο συστήματα συνδεδεμένα σε σειρά με συναρτήσεις μεταφοράς H1(z), H2(z) και κρουστικές αποκρίσεις h1(n)=2+2∙δ(n-1)+δ(n-2), h2(n)=1+δ(n-1) αντίστοιχα. H διαγραμματική υλοποίηση του συστήματος φαίνεται στο Σχ.8.3.3.

Σχήμα 8.3.3.
Ένα σύστημα IIR που περιγράφεται από την εξίσωση διαφορών
![]() (8.4.1)
(8.4.1)
έχει συνάρτηση μεταφοράς H(z) που δίνεται από την σχέση
 (8.4.2)
(8.4.2)
![]() (8.4.3)
(8.4.3)
ή
![]() (8.4.4)
(8.4.4)
Στην σχέση (8.4.3) αν W(z)=B(z)∙X(z), το σύστημα μπορεί να περιγραφεί στο πεδίο του χρόνου από τις σχέσεις
![]() (8.4.5)
(8.4.5)
![]() (8.4.6)
(8.4.6)
Με διαγραμματική υλοποίηση όπως φαίνεται στο Σχ.8.4.1. Αυτός ο τρόπος περιγραφής ονομάζονται ευθείας μορφής τύπου Ι.

Σχήμα 8.4.1
Στην σχέση (8.4.4) αν W(z)=X(z)/Α(z) , το σύστημα μπορεί να περιγραφεί στο πεδίο του χρόνου από τις σχέσεις
![]() (8.4.7)
(8.4.7)
![]() (8.4.8)
(8.4.8)
Με διαγραμματική υλοποίηση όπως φαίνεται στο Σχ.8.4.2. Αυτός ο τρόπος περιγραφής ονομάζονται ευθείας μορφής τύπου ΙI.
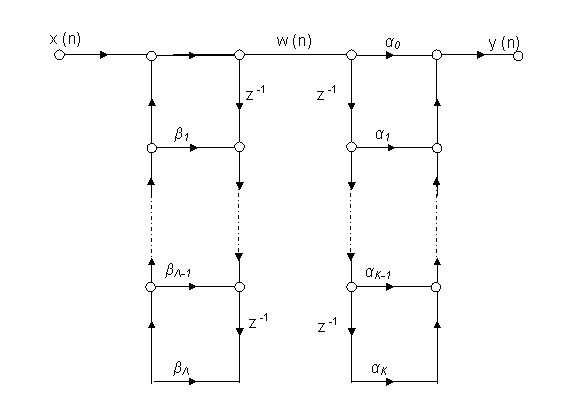
Σχήμα 8.4.2.
Οι μονάδες καθυστέρησης της w(n) μπορούν να ελαττωθούν αν χρησιμοποιηθούν όπως φαίνεται στο Σχ.8.4.3.
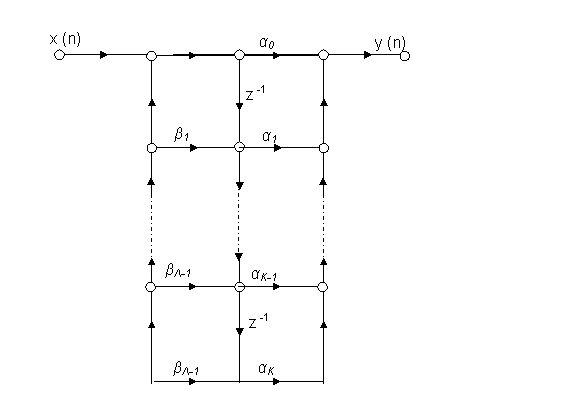
Σχήμα 8.4.3.
Για παράδειγμα το σύστημα με συνάρτηση μεταφοράς
![]()
Περιγράφεται σύμφωνα με τα παραπάνω ως εξής:
Με ευθεία μορφή τύπου Ι.
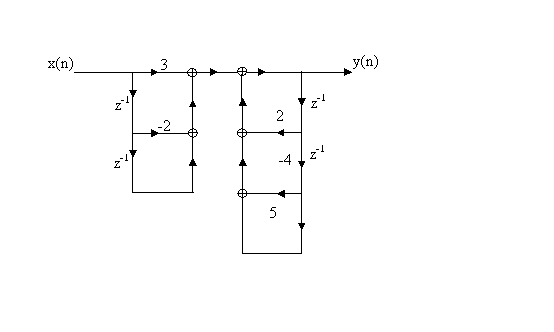
Με ευθεία μορφή τύπου ΙΙ.

ή